
- •4 Дайте гідродинамічну х –ку моделі Раппорта –Ліса
- •6. Дайте коротку х-ку основ теорії не поршневого витіснення нафти водою
- •7. Дайте коротку х-ку основ теорії поршневого витіснення нафти водою
- •84Поясніть принцип поширення моделі поршневого витіснення нафти водою на шарово-неоднорідний пласт
- •88 Поясніть суть методів визначення коефіцієнтів фахових проникностей за результатами лабораторних досліджень стаціонарної фільтрації і витіснення нафти водою.
- •96 Чим відрізняються проект дослідно-промислової розробки і проект розробки родовища?
- •116 Як виконується практична робота із чисельною моделлю процесу розробки нафтових родовищ.
- •118Як здійснюється вибір математичної моделі фільтрації для прогнозування технологічних показників розробки родовища? поясніть
- •120 Як здійснюється схематизація умов нафто вилучення для одно- і двовимірних моделей?
- •125 Які питання розробляються в комплексному плані (проекті) дослідної або дослідно-промислової розробки родовища чи його частини?
- •126 Які спеціальні псевдофункції вводяться в чисельну математичну модель для схематизації пласта, по товщині і розмірності моделі і поясніть
4 Дайте гідродинамічну х –ку моделі Раппорта –Ліса
Модель
двофазної фільтрації з урахуванням
капілярних сил називають моделлю
Раппопорта – Ліса.
Для одновимірного витіснення нафти
водою без урахування сили гравітації
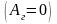 таку модель запропонували Л.Раппопорт
і В.Ліс 1953 року (рівняння
Раппопорта – Ліса),
тобто
таку модель запропонували Л.Раппопорт
і В.Ліс 1953 року (рівняння
Раппопорта – Ліса),
тобто
 . (12.79)
. (12.79)
Якщо в моделі Баклея – Леверетта капілярні сили побічно враховуються через коефіцієнти фазових проникностей, то в моделі Раппопорта – Ліса стрибок капілярного тиску задається у вигляді експериментальної функції насиченості (функції Леверетта).
Модель Баклея – Леверетта, враховуючи фазові проникності для нафти і води, які певним чином залежать від капілярних сил, все-таки не дає змоги описати процеси фільтрації незмішуваних рідин, коли сам рух рідин зумовлюється дією капілярних сил.
Дія капілярних сил проявляється в основному поблизу фронту витіснення, де градієнти насиченості дуже великі. Аналіз показує, що капілярні сили “розмазують” фронт, тому в разі їх урахування стрибок насиченості відсутній, а насиченість водою змінюється безперервно до насиченості зв’язаною водою.
Експериментами
було виявлено, що за постійної швидкості
витіснення
 розподіл насиченості в перехідній зоні
поблизу фронту витіснення не змінюється
в часі, тобто утворюється так звана
стабілізована
зона.
Вона переміщається, не змінюючи своєї
форми. Рух у стабілізованій зоні
відповідає граничному розв’язку
рівняння (12.76), коли розподіл насиченості
не залежить від граничних умов. Розподіл
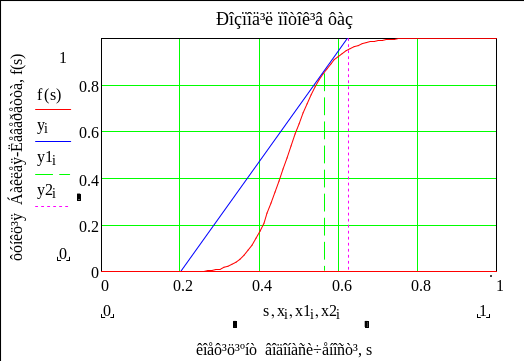
насиченості у стабілізованій зоні є
усталеним (рис. 12.7), тобто не залежить
від часу. Позаду стабілізованої зони
розподіл насиченості описується моделлю
Баклея – Леверетта.
розподіл насиченості в перехідній зоні
поблизу фронту витіснення не змінюється
в часі, тобто утворюється так звана
стабілізована
зона.
Вона переміщається, не змінюючи своєї
форми. Рух у стабілізованій зоні
відповідає граничному розв’язку
рівняння (12.76), коли розподіл насиченості
не залежить від граничних умов. Розподіл
насиченості у стабілізованій зоні є
усталеним (рис. 12.7), тобто не залежить
від часу. Позаду стабілізованої зони
розподіл насиченості описується моделлю
Баклея – Леверетта.
Знайдемо
розв’язок рівняння (12.76) стосовно
прямолінійно-паралельного потоку.
Вводимо швидкість руху фронту витіснення
 .
Робимо заміну змінних
.
Робимо заміну змінних
 , (12.80)
, (12.80)
а відтак шукаємо розв’язок (12.76) у вигляді:
 . (12.81)
. (12.81)
Відповідно до цього перетворюємо рівняння (12.79), знайшовши із рівняння (12.81) з урахуванням рівняння (12.80) величини:
 , (12.82)
, (12.82)
тобто
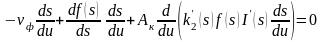 . (12.83)
. (12.83)
Інтегруючи рівняння (12.83) по u, отримуємо:
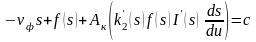 , (12.84)
, (12.84)
де с – постійна інтегрування.
Оскільки позаду стабілізованої зони зміна насиченості описується моделлю Баклея-Леверетта, а рух у перехідній зоні є усталеним з координатою u, то граничні умови мусять бути такими:
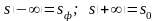 , (12.85)
, (12.85)
де
sф
і s0
– насиченості відповідно за і перед
стрибком насиченості, які пов’язані
між собою співвідношенням (12.67), причому
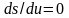 .
.
Тоді із рівняння (12.84) знаходимо постійну інтегрування
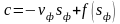 , (12.86)
, (12.86)
а друга умова (12.85) виконується автоматично, так як sф і s0 пов’язані між собою.
Із рівняння (12.84) з урахуванням виразу (12.86) знаходимо
 (12.87)
(12.87)
Проінтегрувавши
рівняння (12.87) по u
від u1
до u
та відповідно по s
від s1
до s,
де
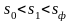 ,
і врахувавши, що
,
і врахувавши, що
 ,
отримуємо розв’язок рівняння (12.79) у
вигляді:
,
отримуємо розв’язок рівняння (12.79) у
вигляді:
 . (12.88)
. (12.88)
Рівняння (12.88) описує розподіл насиченості в перехідній зоні нескінченної довжини, що є наслідком умов (12.85), а значить відсутні точки змикання отриманого розв’язку з розподілом Баклея-Леверетта.
Якщо взяти значини насиченостей не рівні sф і s0, а близькі до них, то виявляється, що ширина перехідної зони є пропорціональною величині
 (12.89)
(12.89)
або
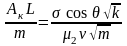 . (12.90)
. (12.90)
Зауважуємо,
що рівняння (12.76) має також, окрім розв’язку
(12.88), точні автомодельні розв’язки, які
існують за спеціально вибраної сумарної
швидкості фільтрації
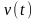 .
.
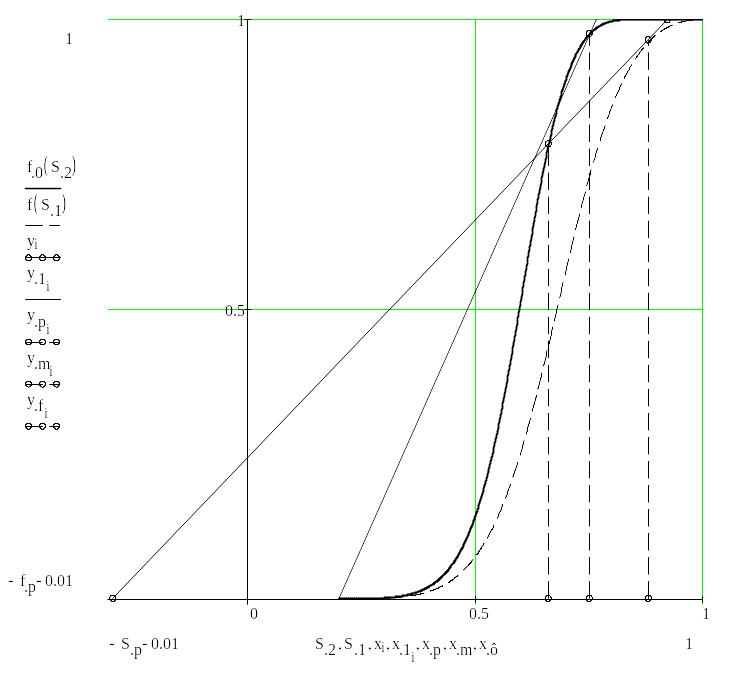
Модель Раппопорта – Ліса дає змогу описати процеси фільтрації незмішуваних рідин, коли сам рух рідин зумовлений дією капілярних сил, зокрема процеси прямоплинного та протиплинного капілярного просочування (рис. 12.8).
У разі протиплинного капілярного просочування нафта у взірці гідрофільного пористого середовища, який занурено у воду, під дією капілярних сил заміщається водою, причому рух їх відбувається в протилежних напрямах. Вода входить дрібними порами, а нафта виходить більшими порами, вспливаючи на поверхню води.
У разі прямоплинного капілярного просочування насичений нафтою взірець гідрофільного пористого середовища всмоктує воду з одного кінця, а нафта виходить із взірця через другий кінець. Відзначаємо, що може спостерігатися і комбіноване (прямоплинно - протиплинне) просочування.
Виникає
питання про області застосування моделей
Баклея – Леверетта та Раппопорта – Ліса.
Область застосування моделі
Баклея – Леверетта одержується
із моделі Раппопорта – Ліса, коли
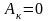 .
Величину
.
Величину
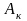 називають капілярним
числом
(зазначимо, що відомо багато різних
записів капілярного числа). Оскільки
називають капілярним
числом
(зазначимо, що відомо багато різних
записів капілярного числа). Оскільки
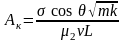 ,
,
то величина в першу чергу визначається характерним розміром L області фільтрації. Оцінимо величину капілярного числа . Беремо: = 25 мН/м (для нафти і води); cos = 1; 2 = 2,5 мПас; т = 0,1; k = 10-13 м2; v = 10-5 м/с. Тоді
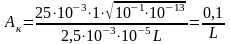 .
.
Якщо L = 0,1 м (лабораторний керн чи фронт витіснення), то 1, а в разі L = 102 – 104 м (відстань між свердловинами в пласті) = 10-3 – 10-5. Тобто в разі великомасштабного розгляду двофазної фільтрації між свердловинами можна нехтувати капілярними силами і брати модель Баклея – Леверетта. Для вивчення розподілу насиченості на фронті витіснення необхідно врахувати капілярні сили, використовуючи модель Раппопорта – Ліса. Звідси випливає, що загально використовувана теорія двофазної фільтрації, в основі якої лежить модель Баклея – Леверетта, є асимптотичною теорією, бо відповідає малим значинам капілярного числа.
Силою
гравітації (ваги) можна нехтувати, якщо
 ,
оскільки гравітаційне
число
,
оскільки гравітаційне
число
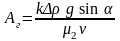 ,
то цьому відповідає умова
,
то цьому відповідає умова
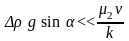 .
.
