1.8. Симплекс-метод решения задачи линейного программирования.

1.8.1. Пример решения задачи линейного программирования симплекс-методом.

Рассмотрим однородную задачу ЛП из примера №1 п. 1.5.:

(1)

Добавив к левым частям системы неравенств соответствующие балансовые переменные преобразуем задачу (1) в каноническую форму:

(2)

Для удобства и единообразия запишем определение целевой функции в виде уравнения:

(3)

Запишем (2) и (3) в виде первой симплекс таблицы:

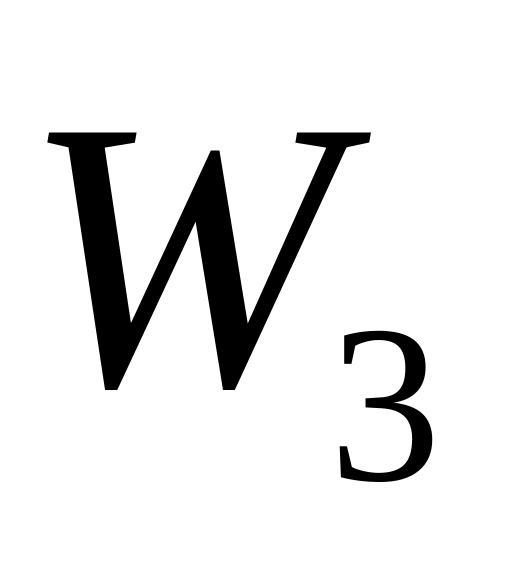
0	1	1	1	0	0	8
0	- 2	3	0	1	0	9	(4)
0	2	- 1	0	0	1	10
1	- 4	- 3	0	0	0	- 1

Первые три строки таблицы (4) содержат по сути расширенную матрицу системы линейных уравнений (2), к которой слева приписан столбец переменной . Последняя строка, называемая индексной, содержит уравнение (3). Буквой , как обычно, обозначен столбец свободных членов. Отметим, что таким образом составленная таблица (4) называется симплексной, поскольку задача (2) имеет симплексную форму. Напомним, что это означает, что во-первых, матрица системы (и таблица (4)) содержат т базисных столбцов (столбцы ), где т - число уравнений (в данном случае ); во-вторых, все элементы столбца свободных членов неотрицательны (это числа 8, 9 и 10), кроме, возможно, элемента индексной строки; в- третьих, целевая функция зависит только от свободных переменных ( и ). Последнее верно, поскольку в базисных столбцах ( ) в индексной строке находятся только нули. Первая симплекс-таблица (4) определяет первое опорное решение. Напомним, что опорное решение является допустимым базисным решением, и, следовательно, свободные переменные и равны нулю: и .

Далее, переменная определяется первой строкой таблицы (4), которая является сокращённой записью первого уравнения системы (2). При оно принимает вид:

Вторая строка таблицы определяет переменную

Третья строка определяет :

Значение целевой функции определяем по индексной строке:

В дальнейшем мы покажем, что оптимальное решение канонической задачи ЛП является опорным, и, следовательно, его следует искать среди опорных решений. Симплекс-таблица (4) и дает одно из таких решений. Как проверить, является ли оно оптимальным? Оказывается, просто. Как мы увидим далее, если коэффициенты целевой функции канонической задачи ЛП неположительные: ,- и функция зависит только от свободных переменных, то соответствующее опорное решение является оптимальным.

Но условие означает, что коэффициенты индексной строки, стоящие в столбцах свободных переменных, должны быть неотрицательны: поскольку индексная строка соответствует уравнению: , - и содержит коэффициенты с противоположным знаком.

Мы видим, что в таблице (4) условие неотрицательности всех элементов индексной строки (разумеется, кроме правой части , стоящей в столбце свободных членов) не выполнено. Более того, оба столбца свободных переменных и содержат в индексной строке отрицательные элементы: - 4 и -3, - соответственно.

Выберем любой из этих столбцов, например, первый и назовем его ведущим. Определим для каждого так называемое допустимое отношение следующим образом. Если в - ой строке ведущего столбца стоит неположительный элемент, то положим если же этот элемент то положим

,

где - номер ведущего столбца.

В нашем случае и допустимые отношения соответственно равны:

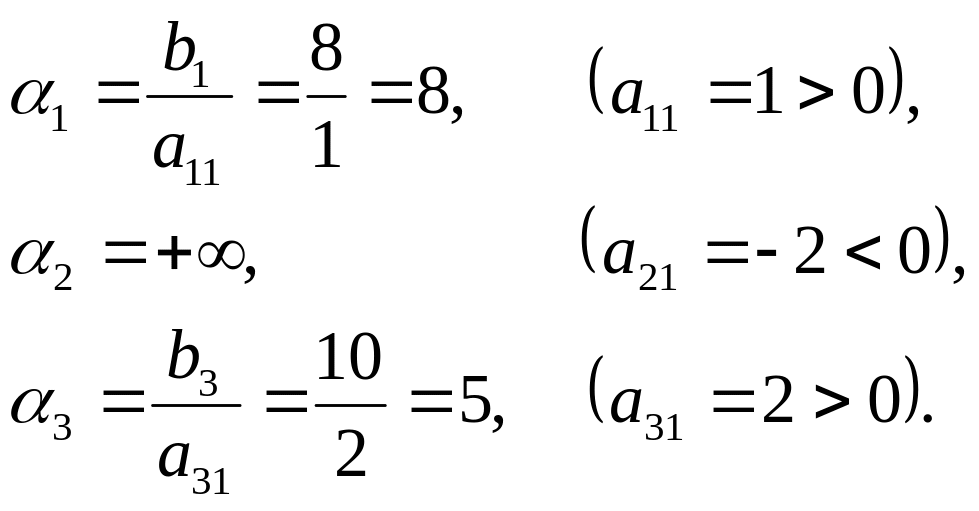
Добавим к симплекс-таблице (4) столбец :

0	1	1	1	0	0	8	8
0	- 2	3	0	1	0	9		(5)
0	2	- 1	0	0	1	10	5
1	- 4	- 3	0	0	0	- 1

В таблице (5) отрицательный элемент – 4 ведущего столбца взят в рамочку, для того чтобы выделить ведущий столбец. Можно, разумеется, выделить этот столбец и любым другим разумным образом: цветом, шрифтом и т.п.

Среди всех допустимых отношений найдем наименьшее: .

Наименьшее допустимое отношение соответствует третьей строке таблицы, которую мы теперь объявляем ведущей строкой. На пересечении ведущей строки и ведущего столбца стоит ключевой элемент таблицы. В нашем случае это Выделим в таблице (5) минимальное допустимое отношение и ключевой элемент, рамочкой:

0	1	1	1	0	0	8	8
0	- 2	3	0	1	0	9		(6)
0	2	- 1	0	0	1	10	5 =
1	- 4	- 3	0	0	0	- 1

Дальнейшая наша цель состоит в том, чтобы преобразовать методом Гаусса таблицу (6) в новую симплекс-таблицу, первый столбец который стал бы базисным, содержащим число 1 в ведущей (третьей) строке.

Вначале разделим ведущую строку на ключевой элемент:

0	1	1		1	0	0	8
0	- 2	3		0	1	0	9		(7)
0	1			0	0		5
1	- 4	- 3		0	0	0	- 1

В таблице (7) мы не заполняем столбец , поскольку он нужен, только для того, чтобы определить ведущую строку, что мы уже сделали. Мы выделили только ключевой элемент, так как он определяет одновременно и ведущую строку (третью) и ведущий столбец (первый).

Проделаем теперь следующие преобразования Гаусса:

1. вычтем из первой строки ведущую (третью) строку;

2. прибавим ко второй строке ведущую, умноженную на 2;

3. прибавим к индексной строке ведущую, умноженную на 4.

В итоге получим новую таблицу:

0	0			1	0		3
0	0	2		0	1	1	19		(8)
0	1			0	0		5
1	0	- 5		0	0	2	19

Нетрудно видеть, что мы получили симплекс-таблицу. Действительно, в таблице (8) после перестановки столбца со столбцом в последних трех столбцах получается единичная матрица; столбец свободных членов неотрицателен; целевая функция зависит только от свободных переменных и

Отметим, что столбец , став базисным, вытеснил «из базиса» столбец . В силу этого обстоятельства проделанный процесс называют операцией однократного замещения. В данном случае эта операция состояла из последовательности элементарных преобразований Гаусса 1), 2) и 3).

Таким образом, получена вторая симплекс-таблица (8), которой соответствует второе опорное решение. Переменные и - свободные и, следовательно, и . Поскольку первое уравнение имеет вид.

то значение базисной переменной равно 3: . Базисная переменная определяется вторым уравнением:

а базисная переменная определяется третьим уравнением (так как в столбце единица стоит в третьей строке):

Итак, , - второе опорное решение. Новое значение целевой функции определяется индексной строкой:

Это опорное решение также не является оптимальным, что следует из того, что в индексной строке таблицы (8) имеется отрицательный элемент (-5) во втором столбце, который мы выберем теперь в качестве ведущего столбца. Затем найдем ведущую строку с минимальным допустимым отношением и ключевой элемент:

0	0		1	0		3	2
0	0	2	0	1	1	19	9,5	(9)
0	1		0	0		5
1	0	- 5	0	0	2	19

Разделим ведущую строку (первую) на ключевой элемент :

0	0	1			0		2
0	0	2		0	1	1	19	(10)
0	1			0	0		5
1	0	- 5		0	0	2	19

Выполним теперь следующие преобразования Гаусса:

1. вычтем из второй строки первую, умноженную на 2;

2. прибавим к третьей строке первую, умноженную на ;

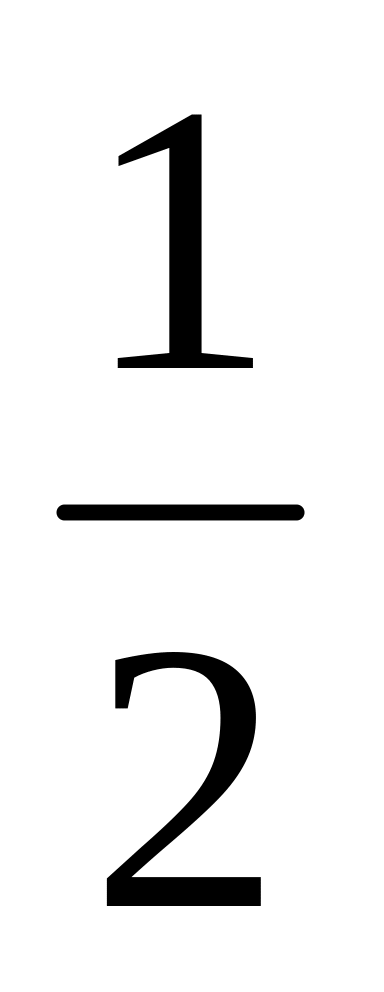3. прибавим к индексной строке первую, умноженную на 5. В результате получим третью симплекс-таблицу:

0	0	1			0		2
0	0	0			1		15	(11)
0	1	0			0		6
1	0	0			0		29

Ей соответствует третье опорное решение:

- и значение целевой функции .

Поскольку индексная строка таблицы (11) не содержит отрицательных элементов, полученное опорное решение будет оптимальным: и (12) При этом Здесь мы звездочками помечаем оптимальные значения переменных.

Таким образом, задача (2) и с ней задача (1) решены.