1.6. Выпуклые множества на плоскости и в пространстве.

Определение 1. Множество А Rⁿ называется выпуклым, если с любыми своими двумя точками А оно содержит целиком отрезок их соединяющий:

А А. (1)

Пусть два вектора на плоскости х О у и пусть точка лежит на отрезке . Тогда вектор колинеарен вектору , направлен в одну сторону с ним и не превосходит его по длине. Эти условия могут быть записаны в виде равенства:

, (2)

где

Векторное равенство (2) равносильно системе:

(3)

Система (3) может быть преобразована в равносильную систему:

(4)

где Обозначим Тогда (4) примет вид:

(5)

где

В векторном виде система (5) примет вид:

где (6)

Определение 2. Выпуклой (линейной) комбинацией векторов называется выражение вида:

где все и

Равенство (6) показывает, что каждая точка отрезка является выпуклой комбинацией векторов

Теорема 1. Пересечение любого числа выпуклых множеств является выпуклым множеством.

Доказательство. Пусть - любое семейство выпуклых множеств. Пусть А – их пересечение:

Покажем, что множество А – выпукло. Пусть Тогда для каждого , поскольку А – пересечение всех . Так как - выпукло, то вместе с точками оно содержит и соединяющий их отрезок:

для всех А_i.

Но, отсюда, очевидно, следует, что каждая точка отрезка (а значит и сам отрезок) принадлежит пересечению множеств , то есть множеству А. Итак, А – выпуклое множество. Что и требовалось доказать.

Определение 3. Выпуклой оболочкой множества называется такое выпуклое множество , что:

1. ,

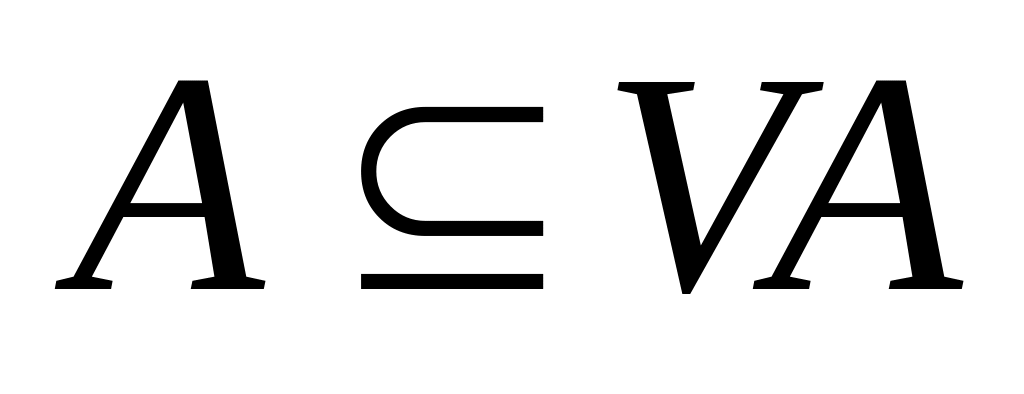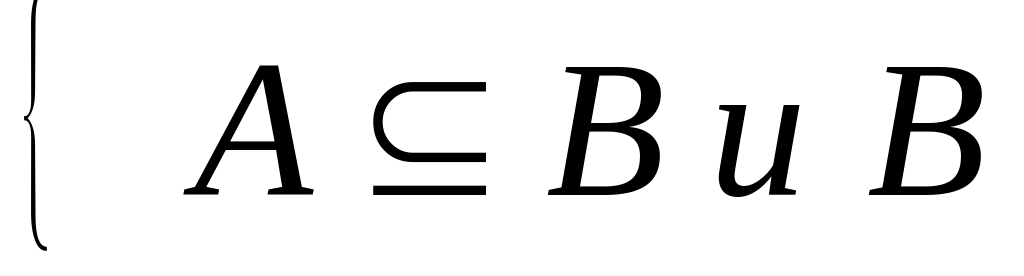2. - выпукло .

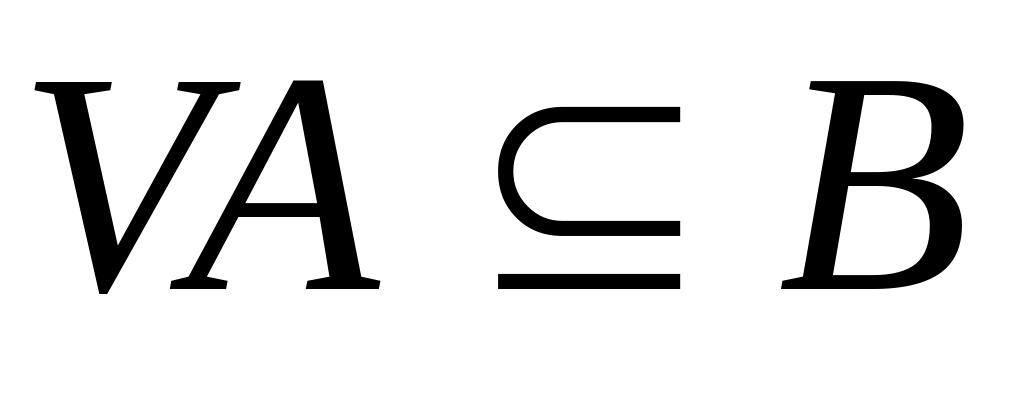Лемма 1. Выпуклая оболочка множества А совпадает с пересечением всех выпуклых множеств, содержащих А.

Доказательство. Пусть В₀ – пересечение всех выпуклых множеств, содержащих А. Тогда очевидно В₀, содержит А. С другой стороны по теореме 1 множество В₀ само выпукло. Отсюда следует, что В₀= VA, поскольку выполнены свойства 1) и 2).

Лемма 2. Отрезок является выпуклой оболочкой своих концов .

Доказательство. Пусть , то есть множество А состоит из двух элементов . Отрезок является выпуклым множеством и содержит А. С другой стороны каждое выпуклое множество В, содержащее А, содержит по определению выпуклости и весь отрезок . Тем самым показано, что ч т.д.

Лемма 3. Если выпуклое множество содержит векторы , то оно содержит и любую их выпуклую комбинацию:

где

Доказательство. Докажем это по индукции. Для двух точек утверждение леммы практически было доказано выше, поскольку множество выпуклых комбинаций совпадает с отрезком и, следовательно, содержится в В. Пусть утверждение справедливо для всех . Покажем, что оно будет также справедливым и для .

Пусть где

Пусть

и .

Тогда

и

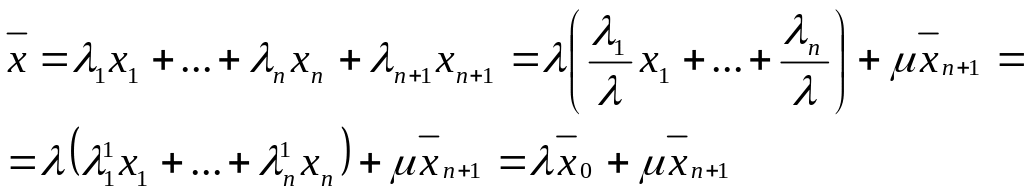где По предположению индукции Так как и то . Лемма доказана.

Теорема 2. Выпуклая оболочка VA множества А Rⁿ совпадает с множеством всех выпуклых комбинаций, состоящих из конечного числа векторов множества А.

Доказательство: Пусть В₀ – множество всех таких комбинаций векторов множества А. Как следует из леммы 3 множество В₀ содержится в любом выпуклом множестве В, содержащем А. Осталось показать, что само В₀ – выпукло.

Пусть - два вектора множества В₀. Тогда , , , .

Пусть - где и Достаточно показать, что , то есть что вектор сам является выпуклой комбинацией векторов из А_0. Но это верно, поскольку:

- выпуклая комбинация векторов - так как и ч.т.д.

Отметим, что треугольник и пирамида являются выпуклыми оболочками своих вершин, и, следовательно, каждая их точка является выпуклой комбинацией векторов-вершин.

Определение. Выпуклая оболочка точки в - мерном линейном пространстве называется симплексом.

Предполагается, что точки лежат в общем положении, то есть не содержатся ни в какой гиперплоскости.

Рассмотрим некоторую точку Возможны следующие случаи расположения точки относительно множества В.

Первый случай. На каждой прямой l , проходящей через , можно найти отрезок , лежащий целиком в В и содержащий внутри себя:

1. 

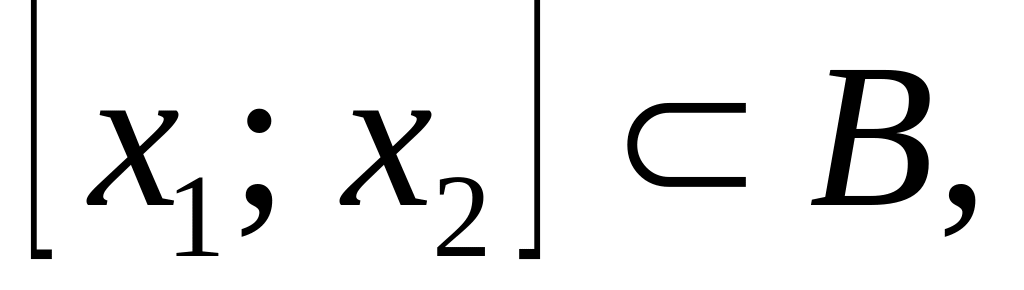
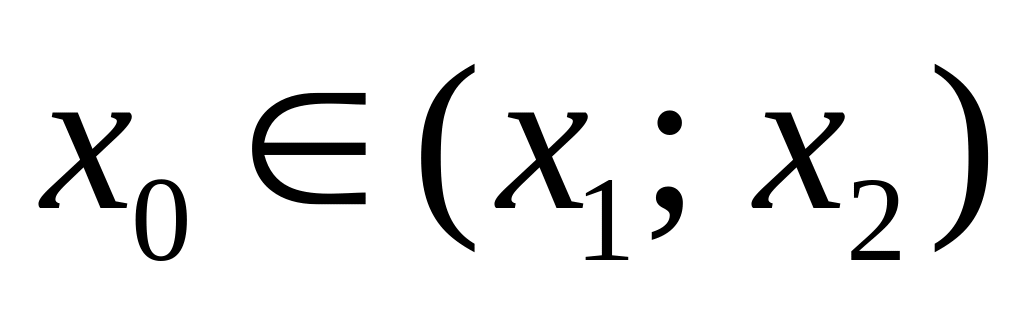2. . (7)

Второй случай. Существует содержащая прямая , на которой не существует отрезка , удовлетворяющего (7).

Если то ясно, что свойством (7) не обладает ни один отрезок . Если для некоторых прямых проходящих через точку отрезок удовлетворяющий (7), существует, а для других прямых нет, то называется граничной точкой множества В. Вблизи граничной точки лежат как точки множества В, так и точки ему не принадлежащие.

Третий случай.

Определение. Пусть точка и ни для одной прямой l содержащей , не существует отрезка , удовлетворяющего (7). В этом случае называется угловой точкой множества В.

Другими словами любой отрезок, содержащий угловую точку внутри себя, обязательно «высовывается» из множества В.

Замечание.

Условие 2) Из (7) можно заменить в предыдущих рассуждениях на условие: , - то есть можно считать, без ограничения общности, что точка является серединой отрезка , действительно, если существует отрезок, содержащий внутри себя, то существует в нем меньший отрезок, для которого точка является серединой.

Определение. Множество называется замкнутым, если оно содержит все свои граничные точки.

Значение угловых точек для описания выпуклого множества в дает следующая теорема, которую мы приводим без доказательства.

Теорема 3. Замкнутое выпуклое множество является выпуклой оболочкой своих угловых точек.