19) Неперервність монотонної функції

Нехай виконані умови: 1)f(x) монотонно зростає(спадає) на [a,b]; 2) множина значень цієї функції суцільно заповнює [α,β]. Тоді f(x) неперервна на сегменті [a,b]. Візьмемо будь-яку т.Xo[a,b], Yo=f(Xo)[α,β]. Покажемо, що f(x) неперервна в т.Xo ( lim(X→Xo) f(X) =f(Xo) ).

X>0: Y1=(f(X)+ )[α,β]. З ІІ теореми Веєрштраса випливає, що X1[a,b]: f(X1)=Y1. Отже, X1>Xo. Позначимо X1-Xo=. Одержимо, що X1=Xo+. Для X(Xo,X1), Xo<Xo+: 0<X-Xo<. Тоді з першої умови теореми випливає, що lim (X→Xo) f(Xo) = f(Xo) < f(X1) = Y1 = f(X)+.

Отже для >0 >0: X(a,b),0<X-Xo<: 0<f(x)-f(Xo)<

Lim(X→Xo+0) f(X)=f(Xo).

Аналогічно можна показати, що ліва границя = f(Xo). Це означає, що в т.X функція є неперервна на сегменті [a,b]. Зауваження: теорема залишається вірною, якщо функція f(x) являється неспадною (не зростаючою). Проміжок може бути як замкнутим, так і відкритим, а також і вся числова пряма.

27) Поняття рівномірної неперервності. Теорема Кантора

Якщо f(x) неперервна на X, то x>0 =(,x)>0 x’X, |x’-x|<: |f(x’)-f(x)|<

Функція f(x) називається рівномірною, якщо для >0 =()>0 x,x’X,|x’-x|<: |f(x’)-f(x)|<. Для рівномірно неперервної – загальне ,а для просто неперервної – своє для кожного x і загального  може не існувати.

Теорема Кантора

Якщо f(x) неперервна на інтервалі [a,b], то вона рівномірно неперервна на цьому сегменті. Нехай f(x) неперервна на [a,b]. Допустимо, що вона не буде рівномірно неперервною.

>0 >0 x,x’[a,b], |x-x’|<: |f(x’)-f(x)|> (1)

Оскільки послідовність {Xn} складається з точок [a,b], то вона обмежена, а значить за Т.Больцана-Веєрштраса з неї можна виділити збіжну підпослідовність {Xnk}.

Lim(k→∞)Xnk=Xo. |Xnk’-Xo|=|Xnk’-Xnk|+|Xnk-Xo|=>limXnk’=Xo; Xo[a,b].

Функція неперервна в цій точці: lim f(Xnk)=f(Xo). |f(Xnk)-f(Xnk’)|→0 (2). (2) протирічить (1). Значить теорема вірна.

Означення: коливанням f(x) насегменті [a,b] називається w=M-m.

Наслідок з теореми Кантора: якщо f(x) неперервна на [a,b], тодля >0 >0, що для  розбиття [a,b] на частинні сегменти з довжиною <, коливання f(x) буде < .

Диференціальне числення.

Критерій існування похідної ф-ії в точці.

Для того щоб існувала скінченна похідна ф-ії в точці необхідно і достатньо, щоб в цій точці існували скінченні однобічні похідні, і вони були рівні. Вони рівні значенню похідної в цій точці.

Правила обчислювання похідної.

Доведення.

ф-ії одержують прирости та

. Звідси

ф-ії y, z, t теж одержать прирости.

.

Переходячи до границі в останніх 3 виразах при маємо:

Т. про приріст ф-ії що має похідну.

Якщо ф-ія y=f(x) в т. x0 має скінченну похідну, тоді приріст ф-ії в ці точці можна записати у вигляді

Доведення.

Оскільки існує похідна ф-ії в т. x0 то за означенням маємо, що існує Звідси маємо, що

. Позначимо

через

Тоді з останньої рівності маємо

де

Необхідна умова існуваннч похідної ф-ії в точці.

Якщо похідна ф-ії в точці існує, то ф-ія f_(x) в т. x₀ неперервна.

Доведення.

Оскільки існує то за т. про приріст ф-ії що має похідну

Звідси маємо, що

а це і означає, що ф-ія f(x) в т. x0 неперервна.

Зауваження: Неперервність ф-ії в точці є умовоє тільки необхідною але не достатньою для існуванняпохідної ф-ії в точці (напр.ф-ія ).

Похідна складеної ф-ії.

Ф-ія f(t) визначена на множині Т, а ф-ія t=g(x) визначена на множ. Х.

Доведення.

Надамо т. x0 приросту , так, щоб Тоді ф-ія t=g(x) одержить в т. х0 приріст t, який дорівнює g(x0+x)-g(x0)=t. Одержане значення t будемо розглядати як приріст аргументу t в т. t0. Тоді ф-ія f(t) в т. t0 одержить приріст

Це є приріст складеної ф-ії в т. х0.

1) Оскільки ф-ія f(t) диференційовна в т. t0 то за т. про приріст ф-ії що має похідну:

2)Оскільки існує похідна ф-ії g в

т. х0 то за необхідною умовою існування похідної, ф-ія g(x) в т. х0 неперервна. Звідси за означ. неперервності ф-ії в т. на мові приростів маємо .

Розглянемо відношення

Переходячи до границі при х0, маємо:

Що і треба було довести.

Похідна оберненої ф-ії.

Т. Якщо існує похідна прямої ф-ії в т. х0 і вона 0, тоді буде існувати похідна оберненої ф-ії x=g(y) в т. y0=f(x0), --

Доведення.

Надамо точці х0 приросту х так щоб (х+х)  Х, тоді ф-ія y=f(x) набуває в т. х0 приросту y=f(x0+x)-f(x0).

Розглянемо відношення 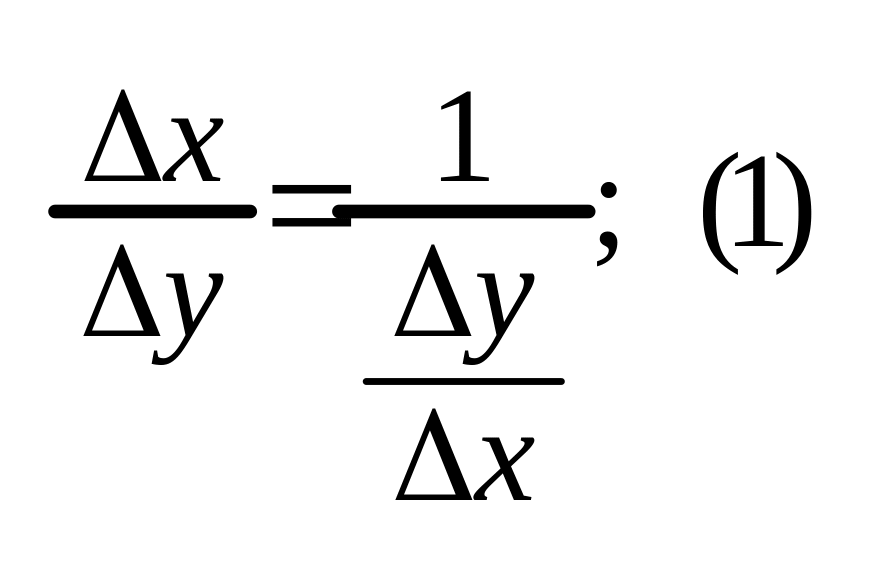Оскільки за умовою існує похідна ф-ії в т. х0, то за необхідною умовою існування похідної

Перейдемо в рівнянні (1) до границі

Похідна ф-ії заданої параметри-чними рівняннями.

Нехай задані дві ф-ії від одної змінної:

Припустимо, що ф-ія строго монотонна і неперервна, тоді ф-ія х буде мати обернену Ф(х)

y=(Ф(х)).Тобто у – складена ф-ія від від х.

Похідна степенево-показникової ф-ії дорівнює сумі двох доданків, перший з яких є похідною від заданої ф-ії як від показникової, а другий – як від степеневої.

Похідна ф-ії заданої неявно

Щоб знайти таку похідну треба продиференціювати це рівняння, враховуючи, що у - це ф-ія від х.

Диференційовність ф-ії в т.

Ф-ія f(x) диференційовна в т. х0 якщо її приріст можна записати у вигляі: у=А*х+х. (1)

де =(х)0, при х0.

А=const. Поділимо обидві частини ріняння (1) на А*х:

у~A*x. при х0, (/А)0.

А це означає що х в рівності (1) є нескінченно малою ф-ією порядку вище ніж х.

Диференціалом називається головна, лінійна відноно х чистина приросту ф-ії в т. х0.

dy=df(x)=Ax=f’(x0)x.

За диференціал незалежної змінної прицмають приріст цієї змінної.

(dx=x) Тому формула перетворю-ється на: dy=f’(x0)dx.

Критерій диференційовності ф-ії в точці.

Для того щоб ф-ія f(x) була диференційовною в т х0 необхідно і достатньо, щоб в т. х0 існувала похідна ф-ії, і іі значення було =А.

Доведення.

Н. Припустимо, що f(x)D(x0)=>

y=A*x+*x, 0, при х0.

Розділимо на х: (y/x)=A+;

Перейдемо до границі при х0

Д. Припустимо, що існує , тоді за т. про приріст ф-ії що має похідну: y=f’(x₀)*x+*x

y=A*x+*x ;

А це і означає що ф-ія є диференційовною.

Геометричний зміст диференціала

Диф. ф. в т. дорівнює приросту ординати дотичної проведеної до графіка функції в цій т.

Властивості диференціалів.

U=U(x),V=V(x)D(x)

1) d(U+V)=dU+dV;

2) d(c*U)=c*dU;

3) d(U*V)=dU*V+dV*U;

4) d(U/V)=(dU*V-dV*U)/V²

Доведення (частка)

d(U/V)=(U/V)‘dx=(U‘V-UV‘)/V²dx

=(U‘dxV-UV‘dx)/V²=

=(dUV-UdV)/V²

Властивості інваріантності

Форма диф. не змінюється при заміні незалежної змінної іншою функцією.

Доведення

Нехай y=f(x)  D(x) xX =>

dy=f‘(x)dx (1)

Нехай x=(t), тоді y=f((t))

dy=f‘((t))‘(t)dt=f‘(x)dx (2)

Праві частини рівностей (1) та (2) однакові за формою, отже диф. 1-го порядку має властивість інваріантності.

Зауважимо, що за змістом формули різні: в правій частині (1) dx–

константа, а в (2) dx – функція.

Похідні вищих порядків

Похідною n-го порядку називається похідна від похідної n-1 порядку.

Властивості похідних вищих порядків

Якщо ф-ї U=U(x) та V=V(x) мають в т. х похідні n-го порядку, то ф-ї UV, CU, UV теж мають похідні n-го порядку.

Формула Лейбница

Диференціали вищих порядків

Для того, щоб в точці існував диф. n-го порядку достатньо щоб ф-я була диференційовна n-раз в точці х, а х була б незалежною змінною, або деякою функцією від змінної t.

наприклад (x=(t)).

Диференціали вищіх порядків не мають властивості інваріантності.

Доведення:

1) dx=x-const

d²x=d(d(x))=0 dⁿx=d²x=0

d²y=d(d(y))=d(f‘(x)dx)=d(f‘(x))dx=

f‘‘(x)dxdx=f‘‘(x)dx²

2) x=(t)

dxx­

d²x0 dⁿx0

d²y=d(d(y))=d(f‘(x)dx)=

d(f‘(x))dx+f‘(x)d²x=

f‘‘(x)dx²+f‘(x)d²x

Порівнюючи (1) та (2) => Диференціали вищіх порядків не мають властивості інваріантності.

Теорема Ферма

Якщо ф-я диф. в деякому околі т. х₀ і досягає в ній екстремума, то похідна = 0.

Доведення:

Нехай ф. досягає в екстремума в т. х₀, тоді існує окіл т. х₀, такий, що для х околу знач. ф.

y=f(x)-f(x₀)<0

Оскільки  f‘(x₀), то f‘(x+0₀)

f‘(x₀-0), та f‘(x+0₀)=f‘(x₀-0)

=> f‘(x₀)=0 (що й треба дов.)

Теорема Ролля

Нехай f(x) неперер. на [a,b] і диф. на (a,b),

f(a)=f(b), тоді  с  [a,b]:f‘(c)=0.

Доведення:

за 2-ю теор. Вейєрштрасса вона досягає inf (m) i sup (M), тоді:

1) M=m => f(x)-const => f‘(x)=0

2) M>m f(a)=f(b) => M чи m  внурішній частині сегмента, тоді за теор. Ферма f‘(x)=0.

Теорема Ла-Гранжа

Нехай f(x) неперер.на [a,b] і диф. на (a,b), тоді

 с(a,b): f‘(c)=(f(b)-f(a))/(b-a)

Доведення:

Введем допоміжну ф-ю:

вона задовольняє умови теор. Ролля

1) непер. на [a,b]

2) диф. на (a,b)

3) (a)=(b)=0

тоді  с(a,b): ‘(c)=0

‘(x)=f‘(x)-(f(b)-f(a))/(b-a)

‘(c)=f‘(c)-(f(b)-f(a))/(b-a)

=> f‘(c)=(f(b)-f(a))/(b-a)

Теорема Коші

Нехай f(x),g(x) неперер.на [a,b] і диф. на (a,b), g(x)0 x(a,b), тоді

g(b)=g(a),тоді ф-я задав. умови теор. Ролля =>  (a,b): g()=0, це суперечіть умові => g(b)-g(a)0.

Введем допоміжну ф-ю:

вона задовольняє умови теор. Ролля

1) непер. на [a,b]

2) диф. на (a,b)

3) (a)=(b)=0

тоді  с(a,b): ‘(c)=0