Ч ислова послідовність це закон чи правило, за яким кожному натура-льному числу n відповідає число

. Символічно позначається .

Ч ислова посл. назив. обмеж. зверху (знизу) якщо існує таке стале число

таке що кожен член послідо-вності не перевищує число для будь-яких . Число M(m) називається верхньою(нижньою) межею посл. a_n. Якщо ця посл. обмежена зверху (знизу) то для неї існує безліч верхніх (нижніх) меж.

Посл. a_n називається обмеж. якщо вона обмеж. зверху і знизу,

тобто

Найменша із усіх верхніх меж посл. наз. точною верхньою межею цієї посл. познач. Sup{a_n}. Аналогічно і Inf{a_n}.

Число m наз. Sup{a_n} якщо

Число m наз. Inf{a_n} якщо

Посл. – обмеж.., якщо

Необмеж, якщо

Нескінченно малі та великі послідовності

Послідовність неск. мала:

1)Будь яка неск. мала послідовність є обмеженою:

Нехай К=max{є,|a₁|,|a₂|...|a_n|}

тоді {a_n}- обмеж.

2)Сума неск. малих послідовно-стей є неск. малою.

Доведення.

{Xn},{Yn} – н.м. посл., звідси

N=max(N1,N2), тоді . Розглянемо

отже {Xn+Yn} – н. м. посл.

Наслідок 1:

Сума(Різниця) дов. числа неск. малих послідовностей є неск. малою.

3) Добуток неск. малої на обме-жену є н. м.

Доведення.

Нехай x_n-обмежена,

y_n-н.м.

Наслідок 2:

Частка двох неск. малих може бути:

1) неск. малою

2) неск. великою

3) збіжною

4) розбіжною

Лема 3:

а – границя {x_n}, якщо {x_n-a} – неск. мала.(док. гр.)

Наслідок 3:

Якщо {x_n} збігається до а, то загальний елемент цієї посл. x_n=a+a_n

Лема 4:

Якщо кожен елемент неск. малої посл. дорівнює С, то С=0

Доведення:

x_n=c – неск.мала.

Нехай =с2,тоді

NN:nN,c<c/2(запереч.)

Теорема 1(зв‘язок н.в. н.м.):

Для того, щоб 1/a_n була неск. великою, необхідно і достатньо, щоб a_n була неск. малою.

1. Достатність:

a_n – неск. мала, дов. 1/ a_n

Нехай для А є= 1/А

2. Необхідність аналогічно.

Границя числової посл.

Число а-границя числ. посл. x_n, якщо {x_n-a}-н.м.

>0N:nN:{x_n-a}<

a-<x_n<a+

Збіжні послідовності

Якщо число а є границею {Xn}, то посл {Хn-а} – н. м. Позначимо

{Хn-а} через , звідси .

Властивості:

1. Збіжна посл. має одну границю.

П рипустимо, що існує число b – границя посл. {Xn}. Оскільки

то

д е - н. м. Оскільки за припу-щенням то

віднімемо: .Оскільки

{ } і { } – н. м. то посл. { - } – н. м. а за останньою власт.н.м. посл. маємо, що b-a=0

тобто b=a

2. Будь-яка збіжна посл. є обмеженою.

Припустимо що {Xn} – збіжна, і , тоді {Xn-a} – н. м.

Нехай {Xn-a}= , звідси

.

Оскільки { } – н. м. то за власт. н. м. посл. вона є обмеж.

тоді

а це і означає що {Xn}- обмеж

3. {x_n} збіг. до a, {y_n} до b, тоді {x_n+y_n} збіг. до a+b.

4. Різниця. 5. Добуток.

6. Частка.

Перехід до границі в нерівностях.

1)Якщо границя {Xn} рівна а, і

тоді a>=b(b>=a)

Доведення

Припустимо, що всі члени послідовності але

Оскільки за припущенням то за означенням.

маємо, що для числа

Із останньої нерівності маємо, що починаючи з номера N Xn<b, що суперечіть умові.

2)(7). x_n=<y_n a=<b

Доведення.

Оскільки Xn=<Yn(Xn-Yn)=<0, а звідси за властивістю збіжних посл.

.

8.(Теорема про гран. зажатої посл.)

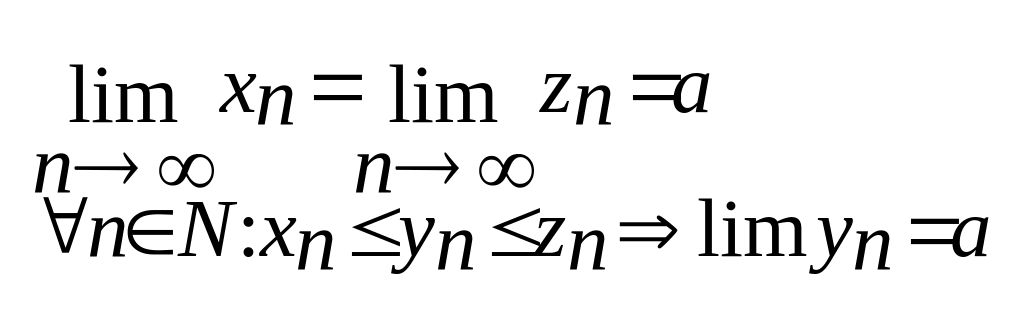
Доведення.

Оскільки то за означ. границі

Оскільки , то ,

Нехай N=max(N1,N2), тоді

одночасно виконуються нерівності (1) і (2).

Враховуючи те що маємо

звідси

Монотонні послідовності

- спадна,

зростаюча, неспадна, незрост.

Ознака збіжності монотонної посл.: Якщо посл{Xn}неспадна або зростаюча і обмеж. зверху, то вона має скінченну границю. В противному випадку границя Аналогічно з незростаючою і спадною.

Доведення.

Припустимо, що {Xn}-неспадна і обмеж зверху. Існує Sup{Xn}=a

звідси за означ. Sup маємо:

Оскільки {Xn} – неспадна, то

Що і треба було довести.

Лема 1(Т. про вкладені відрізки):

Тоді існує єдина т. с.

Покажемо, що може існувати не більше однієї точки:

Нехай є дві точки С та D,C<D

Тоді:

існує лише одна С

Послідовність [an,bn] – не спадна, обмеж. зверху,тоді

Підпослідовності.

Т. про границю підпослідовності.

Якщо {Xn} – є збіжною, то теж збіжна, причому їх границі рівні.

Теорема(Лема) Больцано –Вейєрштрасса

З будь якої обмеженої послідовності можна виділити збіжну підпослідовність.

Зауваження 1:

Аналогічна теорема має місце для необмежених послідовн.

З будь-якої не обмеж. послідовн. Можна виділити нескінченно велику підпосл. Отже з будь-якої посл. Можна виділити або збіжну, або неск. велику підпосл.

Зауваження 2:

Поняття граничної точки можна поширити на необмежену посл., якщо існує підпосл. цієї посл., яка збігається до +8 або –8 =>

Будь-яка посл. має хоча б одну граничну точку.

Послідовність є фундаментальною( Коші ), якщо

Теорема:

Для того, щоб послідовність була збіжною, необхідно і достатньо, щоб вона була фундаментальною.

Функції.

ф-ія – періодична, якщо існує число T=const таке що f(x+T)=f(x), для дов. х із області визн.

1) Якщо ф-ія y=f(x) – періодична, то ф-ія y=A*f(ax+b) теж періодична

причому T=T/A.

2) Якщо y=f1(x)+-f2(x), і періоди T1, T2, то Т=НСК(Т1,Т2).

Елементарна – ф-ія яка задана явно, за допомогою формули, що містить скінченне число арифметичних дій та суперпозицій основних елемен-тарних ф-ій.

Обмеженою знизу (зверху) називається функція (визначена на сегменті (Х)

M(x) xX:f(x)M (f(x)M)

Обмежена на множині-обмежена зверху і знизу.

Число М =sup(f(x)),якщо

1.  xX f(x)M

2.  >0  x₂X:f(x₂)>M-

Число М =inf(f(x)),якщо

1)  xX f(x)M

2)  >0  x₂X:f(x₂)<M+

Границя функції в точці.

f(x) визначена на Х.

Коші:

Гейне:

Ці два визначення еквівалентні

Доведення:

нехай x_n=1/2n 0,n

f(x_n)=cos(2n)=1

f(x_n)=cos(/2+n)=sinn=0

Границя функції на нескінченності та нескінченна границя

1)

2)

Однобічна границя: (ліва)

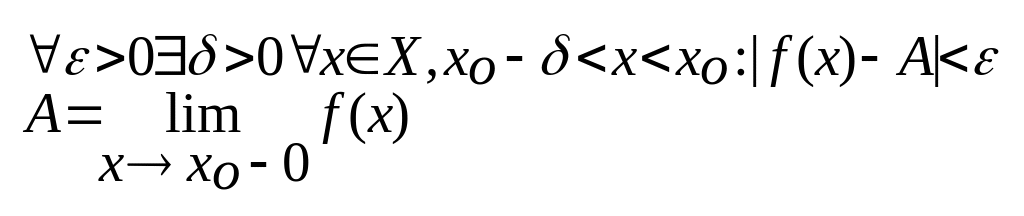
Теорема (про двобічну границю)

Для  необхідно і достатньо, щоб в х₀ існували однобічні границі і були рівними між собою.

Доведення:

(Необхідність):

Нехай існують обидві однобічні границі рівні А.

Із означення границі маємо:

тобто

маємо

отже

(Достатність):

Припустимо

Доведемо 

Оскільки ,то

Оскільки ,то

=min(₁,₂)

тобто

Критерій Коші (для функцій):

Теорема:

Для того, щоб функція в точці x=a мала границю, необхідно і достатньо, щоб:

Властивості функцій, що мають скінченну границю.

1) - то вона єдина

2) => окіл точки х₀ в якому функція обмежена.

3) ,

4)

5) Перша границя

0<x<1/2

sinx=MNtgx=AB

ON=OA=1

Soan=1/2OAMN=1/2sinx

Scoan=x/2OA²=x/2

Soab=1/2OAAB=1/2tgx

Soan<Scoan<Soab

Sinx<x<tgx

Друга границя

Доведення:

Нехай n=[x] => nx<n+1 (1)

1/(n+1)<1/x1/n

(2)

із (1),(2) =>

за теоремою про зажату послідовність:

=>
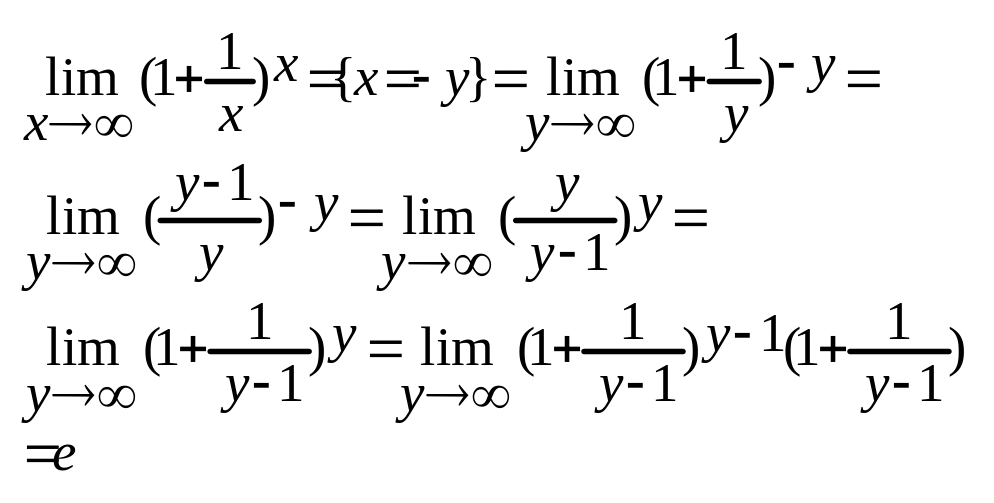