16. Произв элемент ф-ций. Логарифмич диффиринц.

Промежуточный аргумент u

1. (с)’=0

2. (u^a)’=a*u^a-1 в частности ( 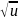)’ = 1/2

3. (a^u)’=a^u*ln a в частности (e^u)’=e^u

4. (log_a u)’=1/u*ln а в частности (ln u)’=1/u

5. (sin u)’ =cos u (cos u)’=-sin u

6. (tg u)’ = 1/cos²u (ctg u)’ = - 1/sin² u

7. (arcsin u)’ =1/ 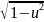(arcos u)’ = - 1/ \

8. (arctg u)’ = 1/1+u² (arcctg u)’ = - 1/1+u²

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций.

Вычислить производную функции . Решение.Применяем логарифмическое дифференцирование:

     

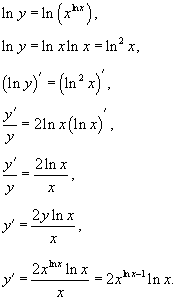
17 Дифференциал ф-ции,геом смысл,св-ва,инвариантная форма записи,приложения

Дифференицал ф-ции y=f(x) в точке х наз главная часть ее приращения,равная произведению производной ф-ции на приращение аргумента dy=f’(x)dx ( диф ф-ции равен произвед производной этой точки на диффиринц незав переменн.)

Геометр смысл:диффер ф-ции у=f(х) в х равен приращению ординаты касательной к графику ф-ции в этой точке,когда х получит приращ

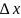
d(u+v)=du+dv d(uv)=v*du+u*dv d(u/v)=(v*du-u*dv)/v² dy=y’_xdx(y=f(x)) dc=0 d(aⁿ)=na^n-1du...

 Пусть y = f(x), x = g(t), т.е у- сложная функция.Тогда dy = f(x)g(t)dt = f(x)dx

 Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала. Однако, если х- независимая переменная, тоdx = x, но,если х зависит от t, то х  dx. Таким образом форма записи dy = f(x)x не является инвариантной 

  Пример. Найти производную функции .Сначала преобразуем данную функцию:

18 Произв и дифф ф-ций высших порядков не инвариантность форм записи

Предположим, что функция f'(x) является дифференцируемой в некоторой точке x интервала (a,b), то есть имеет в этой точке производную. Тогда данную производную называют второй произвоьдной и обозначают f⁽²⁾(x), f''(x) или y⁽²⁾, y''(x). Аналогично можно ввести понятие второй , третьей и т. д. производных. По индукции можно ввести понятие n- ой производной:

y(n) = (y(n-1))'.

(6)

Функцию, имеющую на некотором множестве конечную производную порядка n, называют n раз дифференцируемой на этом множестве. Методика нахождения производных высших порядков предполагает умение находить производные первого порядка, о чем говорит формула (6).

Если u(x), v(x) две дифференцируемые функции, то для нахождения производной их произведения справедлива формула Лейбница

(u(x)v(x))⁽ⁿ⁾ = u⁽ⁿ⁾v+nu^(n-1)v'+(n(n-1)/2)u^(n-2)v''+...+ uv⁽ⁿ⁾ =

= _{k = 0}ⁿC_n^ku^(n-k)v^(k),

где

C_n^k = (n(n-1)(n-2)...(n-k+1))/k!, u⁽⁰⁾ = u, v⁽⁰⁾ = v.

Данная формула Лейбница особенно эффективна в случае, когда одна из перемножаемых функций имеет конечное число отличных от нуля производных и легко вычислить производные другой функции.

Пример 9. Пусть y = e^x(x²-1). Найти y⁽¹⁰⁾. Положим u(x) = e^x, v(x) = (x²-1). Согласно формуле Лейбница

y⁽¹⁰⁾ = (e^x)⁽²⁵⁾(x²-1)+10(e^x)⁽⁹⁾(x²-1)'+(10· 9/2) (e^x)⁽⁸⁾(x²-1)'',

так как следующие слагаемые равны нулю. Поэтому

y⁽¹⁰⁾ = e^x(x²-1)+10e^x2x+(10· 9/2)e^x (2) = e^x(x²+20x+89)

Рассмотрим выражение для первого дифференциала

dy = f'(x)dx.

Пусть функция, стоящая в правой части, является дифференцируемой функцией в данной точке x. Для этого достаточно, чтобы y = f(x), была дифференцируема два раза в данной точке x, а аргумент либо является независимой переменной, либо представляет собой дважды дифференцируемую функцию.

Определение 6 (дифференциал второго порядка). Значение (dy) дифференциала от первого дифференциала (4) при  x = dx, называется вторым дифференциалом функции y = f(x) и обозначается d²y.

Таким образом,

d²y =  (dy)|_{ x = dx}.

Дифференциал dⁿy можно ввести по индукции.

Определение 7. Значение (d^n-1y) дифференциала от(n-1)-го дифференциала при  x = dx, называется n-м дифференциалом функции y = f(x) и обозначается dⁿy.

Найдем выражение для d²y при этом рассмотрим два случая, когда x -независимая переменная и когда x =  (t), то есть является функцией переменной t.

1. пусть x =  (t), тогда d² =  (dy)|_{ x = dx} =  (f'(x)dx)|_{ x = dx} = { (f'(x))dx+f'(x)(dx)}|_{ x = dx} = f''(x)(dx)²+f'(x)d²x.

Итак, d2y = f''(x)(dx)2+f'(x)d2x.

(7)

2. пусть x - независимая переменная, тогда d²y = f''(x)(dx)²,так как в этом случае (dx) = (dx)' x = 0.

Аналогично, по индукции легко получить следующую формулу, если x - независимая переменная:

dⁿy = f⁽ⁿ⁾(x)(dx)ⁿ.

Из этой формулы следует, что f⁽ⁿ⁾ = dⁿy/(dx)ⁿ.

В заключение отметим, что дифференциалы второго и более высоких порядков не обладают свойством инвариантности, что сразу видно из формулы для дифференциала второго порядка (7).

‍‍19. ф-ции заданы параметрически и их диффер

Пусть x =  (t),y =  (t), t [a,b] - достаточно гладкие функции. Тогда говорят, что функция задана параметрически. Примером параметрически заданной функции является уравнение окружности: x = acos t,y = asin t, t [0,2]. Рассмотрим вопрос о нахождении производных y = y(x) по переменной x.

В силу свойства инвариантности формы первого дифференциала следует, что y' = dy/dx, dy = '(t)dt, dx = '(t)dt. Поэтому y'(x) = '(t)/'(t).Используя формулу для второго дифференциала, получим y⁽²⁾(x) = d(y'(x))/dx = ( '(t)/ '(t))'dt/ '(t)dt = ( ''(t)  '(t)- ''(t) '(t))/( '(t))³.

Чтобы вычислить третью производную, запишем y'''(x) в следующем виде y'''(x) = d(y''(x))/dx.

Пример 11. Найти y''(x), если : x+y = e^x-y.Дифференцируем данное уравнение по x, считая y функцией от x. 1+y'_x(x) = e^x-y(1-y'_x(x)),откуда y'_x = (e^x-y-1)/(1+e^x-y)Дифференцируя уравнение еще раз, получим y''_x(x) = e^x-y(1-y'_x(x))²-e^x-yy''_x(x), следовательно, y''_x(x) = (1-y'_x)²e^x-y/(1+e^x-y) = 4e^x-y/(1+e^x-y)³