
- •1. Конечный предел числовой последовательности
- •2 Критерий сходимости монотонной последовательноти
- •4 Теоремы о пределах суммы, произведения, частного сходящихся последоват
- •5 Теоремы о пределах последоват связан неравенств
- •6 Число е
- •8 Основные теоремы о пределах ф-ций
- •9 Замечательные пределы
- •10 Сравнение ф-ции. О и о. Эквиваленты бмф и с-ва
- •12 Точки разрыва
- •13 Непрерывность ф-ции на интервале,отрезке. Формулировка св-в ф-ций, непрер на отрезке
- •14 Производная ф-ции действ переменного,геом смысл и механ смысл. Касательная и нормаль к кривой. Односторон произв. Необх условия сущ производной
- •15 Общие правила диффиринцирования. Дифф сложн ф-ции,обратной ф-ции
- •Произв элемент ф-ций. Логарифмич диффиринц.
- •17 Дифференциал ф-ции,геом смысл,св-ва,инвариантная форма записи,приложения
- •18 Произв и дифф ф-ций высших порядков не инвариантность форм записи
- •20 Теоремы ферма.Роля их геом смысл
- •21Теорема лагранжа геом смыл. Теорема коши
- •22 Правило лопиталя
- •23 Формула тейлора с остаточным членом в формк пеано и лагранжа. Формула маклорена
- •25 Необх и дост усл монотонн ф-ции. Экстремум необх и дост усл
- •26 Необх и дост усл вып(вогн) графика ф-ции. Необх дост усл существ точки перегиба. Асимптоды графика ф-ции
- •27 Открытые и замкн множестка, связаные множества. Область замкнутая область. Связаные области .
- •29 Частные произв и дифф ф-ции неск переменн. Необх и дост усл дифф.
1. Конечный предел числовой последовательности
а- lim {xn} еcли для любого Ԑ>0 найдется натуральн число N что при всех n>N вып нер lxn –al<Ԑ
для
того чтобы последовательность х
n,
n=1,
2, . . ., имела предел, необход и дост, чтобы
для любого Ԑ>0 Ǝ N, что для всех N≤n
b
N≤m
выполнялось нер
![]()
2 Критерий сходимости монотонной последовательноти
Для того что бы xn cходилось необх и дост что б ее верхн и нижн lim совпадали
3 бмп ббп
Бмп – числовая последоват lim = 0
10 cумма 2-х бмп - беск посл 20 произв бмп на огр посл = бесконечн велич (любая бмп ограничена)
Ббп -
![]()
связь:если { хn} — ббп и все ее члены отличны от нуля, то последовательность {1 / xn} бесконечно малая, и, обратно, если {αn} — бмп и все её члены отличны от нуля {αn} ≠ 0, то последовательность { 1 / αn } – бесконечно большая.
4 Теоремы о пределах суммы, произведения, частного сходящихся последоват
![]()
Произведение 2-х сходящ последоват – сходящ послед lim= произвед пределов послед {xn}{yn}
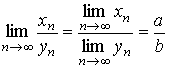 yn
≠ 0
yn
≠ 0
5 Теоремы о пределах последоват связан неравенств
Если xn
≤ yn и
![]() ,
,
![]() ,
то x ≤
y.
,
то x ≤
y.
6 Число е
е- непреново число ≈ 2,72 оно принято за основание натуральных логор
7 конечный lim ф-ции действительно перемен при х⟶а. Бесконечн больш ф-ции при х⟶а. Одностор lim
Гейне: а
- lim значений f(x)
в x0 если для V
последовательностей точек xn
, nϵN
имеющи своим lim х0(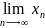 =
x0)
=
x0)
Последовательность
значений ф-ции имеет lim в
a (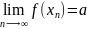 .
Говорят f(x)
при x⟶x0
имеет своим пределом а(
.
Говорят f(x)
при x⟶x0
имеет своим пределом а(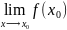 =a)
необходимое условие сущ – ф-ция имеет
конечный предел в данной точке х0
=a)
необходимое условие сущ – ф-ция имеет
конечный предел в данной точке х0
Коши
: а-lim
f(x), хϵХ при
х⟶х0,
если для V
напередзад. числа Ԑ и δ > 0 как только
хϵU(x0δ)
так сразу f(x)ϵU(a
Ԑ)
ɄԐ>0 δ>0 lx-x0l < f(x)=U(x0,δ)
l(f(x)-al <Ԑ=f(x)≤U(a,Ԑ)
ббф если для
V M>0
Ǝδ=δ(M)>0
что для V x
удв нерав 0<lx-x0l<δ
вып нерав lf(x)l>M
(lim f(x)=∞)
Одностор преде́л — предел числовой функции, подразумевающий «приближение» к пред точке с одной стороны
А1 lim
ф-уции слева(справа)в х0если для
VԐ>0
Ǝδ=δ(Ԑ)>0 при хϵ(х0-Ԑ;х0) вып
нерав l f(x)
– A1 l
<Ԑ
(x0;x0+δ) для справа
8 Основные теоремы о пределах ф-ций
Lim(f(x) ±λ(x))= lim f(x) ± lim λ(x) Lim(f(x)*lim(λ(x)) = limf(x)*limλ(x) lim c*f(x)=c*lim f(x)
Lim(f(x))n=(limf(x))n
lim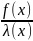 =
=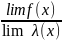
9 Замечательные пределы
1)
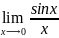 =1 2)
=1 2)
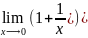 x=e
lim(1+a)1/a=e(x⟶a)
x=e
lim(1+a)1/a=e(x⟶a)
10 Сравнение ф-ции. О и о. Эквиваленты бмф и с-ва
f(x)=λ(x)*g(x)
f(x)
1. Ограниченая
относительно ф-циии
g(x)
в U(х0)
если λ(х) ограничена. Если λ(х) огрвып
нер: lλ(x)l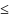 C(const)
C>0
хϵX
C(const)
C>0
хϵX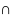 U(x0)
=>lf(x)l
C*lg(x)l
если f(x)
огр относит g(x)
в U(х0)
тозаписывают f(x)=O(g(x))
при х⟶х0
2.того
же порядка что и
g(x)
в U(х0)
если Ǝ С1
и С2>0
что для
U(x0)
=>lf(x)l
C*lg(x)l
если f(x)
огр относит g(x)
в U(х0)
тозаписывают f(x)=O(g(x))
при х⟶х0
2.того
же порядка что и
g(x)
в U(х0)
если Ǝ С1
и С2>0
что для
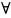 хϵХ
U(х0)
вып нер С2
lλ(х)l
С1
в этом случае для
Х
U(х0)
будет вып С2lg(x)
lf(x)l
C2lg(x)l
в этом случает f(x)=O(g(x))
x⟶x0
и одноврем g(x)=O(f(x))
ф-ции f
и g
одного порядка 3.бмф
относит g(x)
для
хϵХ
U(х0)
вып нер С2
lλ(х)l
С1
в этом случае для
Х
U(х0)
будет вып С2lg(x)
lf(x)l
C2lg(x)l
в этом случает f(x)=O(g(x))
x⟶x0
и одноврем g(x)=O(f(x))
ф-ции f
и g
одного порядка 3.бмф
относит g(x)
для
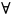 х
U(х0)
если λ(х)беск мал для
Х
U(х0)
4. Эквивалентная ф-ция ф-ции g(x)
для
хϵХ
U(х0)
если lim λ(x)=1(х⟶х0)
если
lim
a/b
=1 (x⟶0)
наз эквивалентными беск мал 10 lim
отноше 2-х бмф не изменится если каждую
или одну заменить эквивалентн ей беск
мал 20разность 2-х эквивал бмф –беск
малая более выс порядка чем каждая из
них 30сумма конечного
числа бмф разных порядков эквивал
слагаемому низшего порядка .что бы
ф-ция была ~ необх и дост f(x)=g(x)+o(g(x))
sinx~tgx~arsinx~arctgx~ex-1~ax-1~ln(1+x)~x
1-cosx~x2/2;loga(1+x)~xlogae;(1+x)k-1~kx,k>0;
х
U(х0)
если λ(х)беск мал для
Х
U(х0)
4. Эквивалентная ф-ция ф-ции g(x)
для
хϵХ
U(х0)
если lim λ(x)=1(х⟶х0)
если
lim
a/b
=1 (x⟶0)
наз эквивалентными беск мал 10 lim
отноше 2-х бмф не изменится если каждую
или одну заменить эквивалентн ей беск
мал 20разность 2-х эквивал бмф –беск
малая более выс порядка чем каждая из
них 30сумма конечного
числа бмф разных порядков эквивал
слагаемому низшего порядка .что бы
ф-ция была ~ необх и дост f(x)=g(x)+o(g(x))
sinx~tgx~arsinx~arctgx~ex-1~ax-1~ln(1+x)~x
1-cosx~x2/2;loga(1+x)~xlogae;(1+x)k-1~kx,k>0;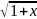 -1~x/2
O.o
- Символы бесконечно малых
-1~x/2
O.o
- Символы бесконечно малых
![]() -
"б.
м. порядка не
ниже
-
"б.
м. порядка не
ниже
![]() относительно
относительно
![]()
11 ф-ции действ переменного непрер в точке их св-ва. Непрер элем ф-ций
действительного переменного — ф-ция, которая совпадает со своим рядом Тейлора в окрестности любой точки области определения.( разложение функции в бесконечную сумму степенных функций) ф-ция f(x) непрерыв в x0 если Ǝlim в этой точке и = знач ф-ции в этой точке lim f(x)=f(x0) x⟶x0
Функция, непрерывная в точке
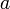 ,
является ограниченной в некоторой
окрестности этой точки.
,
является ограниченной в некоторой
окрестности этой точки.Если функция
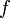 непрерывна
в точке
и
непрерывна
в точке
и
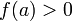 (или
(или
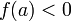 ),
то
),
то
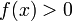 (или
(или
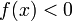 )
для всех
)
для всех
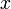 ,
достаточно близких к
.
,
достаточно близких к
.Если функции и
 непрерывны
в точке
,
то функции
непрерывны
в точке
,
то функции
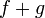 и
и
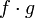 тоже
непрерывны в точке
.
тоже
непрерывны в точке
.Если функции и непрерывны в точке и при этом
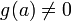 ,
то функция
,
то функция
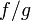 тоже
непрерывна в точке
.
тоже
непрерывна в точке
.
Непрерывность
элем ф-ций Т1( ±,*
2-х непрер ф-ций = ф-ция непрерывная)
Т2(пусть ф-ции u=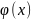 непрер в х0, а у=f(u)
непрер в u0=
непрер в х0, а у=f(u)
непрер в u0=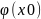 тогда сложная ф-ция а(
тогда сложная ф-ция а(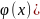 сост
из непрерыв ф-ций, непрер в х0) Т3(если
ф-ция y=f(x)
непрер и строго монотонна на [a;b]
оси Ох то обр ф-ция y=
так ж непрер и монотонн на соответств
отрезке [c;d]
оси Оу) () всякая элементарн ф-ция непрер
в каждой точке в которой она определена
сост
из непрерыв ф-ций, непрер в х0) Т3(если
ф-ция y=f(x)
непрер и строго монотонна на [a;b]
оси Ох то обр ф-ция y=
так ж непрер и монотонн на соответств
отрезке [c;d]
оси Оу) () всякая элементарн ф-ция непрер
в каждой точке в которой она определена
