29. Применение формулы Тейлора для исследования стационарных точек(нашёл только для экстремума):

Покажем, как использовать формулу Тейлора для исследования функции на экстремум.  . Нужно определить, является ли точка   точкой экстремума.

Будем считать, что функция дифференцируема любое нужное нам число раз.

. Пусть  .   — первое такое число, что производная   такого порядка в этой точке не равна 0. По формуле Тейлора с остатком по Пеано, 

. При  .

Заметим, что  , а   — изменяется. Тогда возможны два случая:

•  — чётное:

Тогда 

Если   больше  , то в   минимум, если меньше — то максимум.

•  — нечётное:

 в зависимости от того, с какой стороны   находится от   на числовой оси. Значит, экстремума в точке   нет.

30. Выпуклость и вогнутость графика функции. Точки перегиба. Применение формулы Тейлора для исследования направления выпуклости и перегибов:

График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.

На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).

Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.

31)Асимптоты графика функции.

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.

Асимптоты могут быть вертикальными, горизонтальными и наклонными.

Вертикальные.

Прямая х=а является вертикальной асимптотой графика y=f(x), если lim_x->af(x)=∞, или lim_x->a-o=∞,

или lim_x->a+0f(x)= ∞.

Для отыскания вертикальных асимптот нужно найти те значения х, вблизи которых функция f(x) неограниченно возрастает по модулю. Обычно это точки разрыва второго порядка.

Наклонные.

у=kx+b

Пусть

M(x;y)—произвольная точка кривой y=f(x). По формуле расстояния от точки до прямой находим расстояние от точки М до прямой d=| |.

Условие d->0 , будет выполняться лишь тогда, когда числитель дроби стремится к нулю, т.е.

lim_x->∞(kx-y+b)=0

Отсюда следует, что kx-y+b=a, где а =а(х) бесконечно малая: а->0 при х->∞. Разделив обе части равенства y=b+kx-a на х и перейдя к пределу при х->∞, получаем:

Lim_x->∞ =lim_x->∞( +k- );

Так как b/x->0 и a/x->0, то

k=lim_x->∞y/x. (1)

b=lim_x->∞(y-kx). (2)

Если существует наклонная асимптота y=kx+b, то k и b находятся по формулам (1) и (2).

Верно и обратное утверждение: если существуют конечные пределы (1) и (2) , то прямая является наклонной асимптотой. Если хотя бы один из пределов не существует или равен бесконечности, то кривая наклонной асимптоты не имеет.

В частности, если k=0, то b=lim_x->∞f(x). поэтому y=b – уравнение горизонтальной асимптоты.

Замечание: асимптоты графика функции при X->+∞ и Х->-∞ могут различаться.

32) Пусть задано множество D упорядоченных пар чисел (x;y). Соответствие f,которое каждой паре чисел (x;y)€D сопоставляет одно и только одно число число z€R, называется функцией двух переменных, определенной на множестве D со значением в R, и записывается в виде z=f(x,y) или f:D->R. При этом х и у называются независимыми переменными(аргументами),а z—зависимой переменной (функцией).

Множество D=D(f) называется областью определения функции. Множество значений z в области определения—область изменения функции.(E или E(f)).

Примером функции двух переменных может служить площадь прямоугольника со сторонами х и у: s=xy. область определения функции {(x;y)|x>0 y>0};

Областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Внутренние точки-точки, не лежащие на границе. Область из внутренних точек—открытая. Область с присоединенной к ней границей—это замкнутая(D с чертой сверху).замкнутая область—круг с окружностью.

Значение функции в определенной точке—частное значение функции.

Функция двух независимых переменных допускает геометрическое истолкование. Каждой точке в Oxy соответствует точка в Oxyz , где z0=f(x0;y0)—аппликата точки. Совокупность точек представляет собой некоторую поверхность, отображающую данную функцию.

Функция двух переменных, как и функция одной переменной, может быть задана таблицей, аналитически, графически.

Предел функции двух переменных

Множество всех точек плоскости, координаты которых удовлетворяют: <∂

называется ∂-окрестностью точки M0(x0;y0).(Это все внутренние точки круга с центром М0 и радиусом ∂).

Пусть функция z=f(x,y) определена в некоторой окрестности точки M0(x0,y0),кроме, быть может, самой этой точки. Число А называется пределом функции при х->x0 y->y0, если для любого ɛ>0 cуществует ∂>0 ,что для всех х=/x0 y=/y0 ,удовлетворяющих <∂ выполняется неравенство |f(x,y)-A|< ɛ.

Непрерывность

Функция z=f(x;y) (или f(M)) называется непрерывной в точке M0(xo;y0), если она:

а) определена в этой точке и некоторой ее окрестности,

б)имеет предел Lim_M->M0f(M).

в) Этот предел равен значению функции z в точке M0, т.е.

Функция непрерывная в каждой точке называется Непрерывной в этой области. Если одно из условий не соблюдается—образуется точка разрыва, или даже линия.

33)Рассмотрим функцию двух переменных z = f(x]y), определенную и непрерывную в некоторой области D. Считаем, что точки с координатами (х; у), (х + дх; у), (х; у + ду), (х + Дх; у + ду), где дх, ду — приращения аргументов, также принадлежат области D.

Частными приращениями функции z = f(x;y) по независимым переменным х и у называются разности д_xz = f(x + дx;y) - f(x; у), д_yz = f(x; у + дy) - f(х; у).

Полным приращением функции z = f(x; у), соответствующим приращениям аргументов дх ду, называется разность дz = f(x + дх; у + ду) - f(x; у).

Заметим, что в общем случае дz=/д _xz + д_yz.

Частной производной функции z = f(x; у) по переменным x и у называется предел отношения соответствующего частного приращения д_xz или д_yz к приращению данной переменной, при условии, что приращение переменной стремится к нулю:

Дифференциал функции.

Е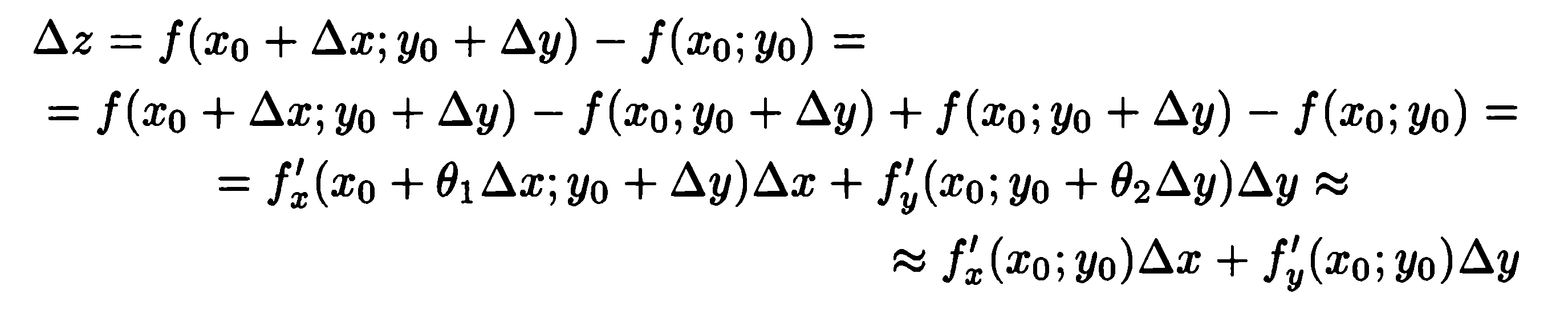 сли Функция f(x;y) обладает частными производными f’ по х и у, непрерывными в точки М0(х0;y0), то теорема Лагранжа для функции одной переменной позволяет получить следующее: (дх и ду ~ 0);

Это выражение представляет собой главную, линейную часть приращения функции и называется дифференциалом этой функции в данной точке.

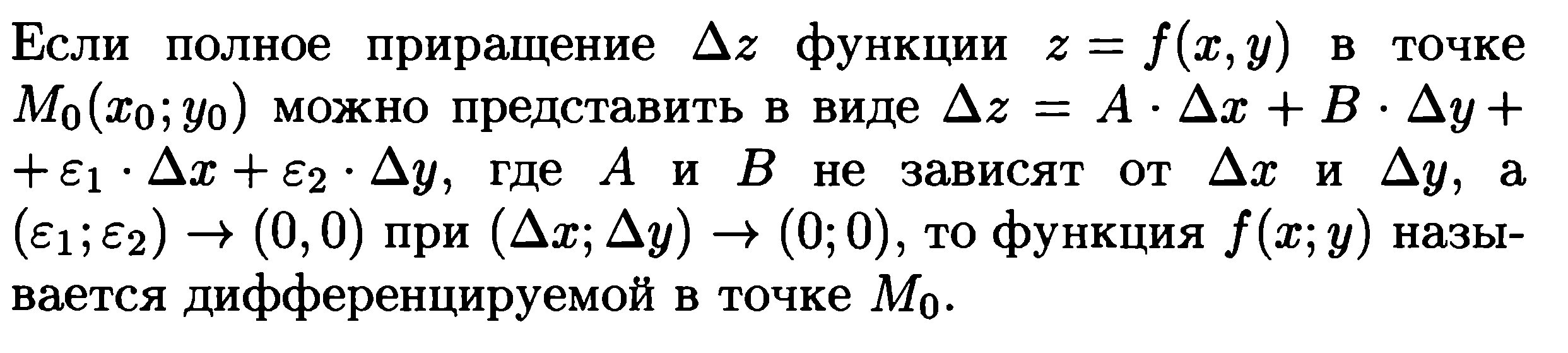
– это Линеаризация функции z=f(x;y) в окрестности точки Mo(x0;y0). При условии, что дельта z ~dz

34)Частные производные высших порядков…

Пусть функция двух независимых переменных u = f (х, у) имеет частные производные: Это, в свою очередь, снова функции двух переменных, которые снова можно дифференцировать, и определяются эти новые производные по той же схеме. Например:

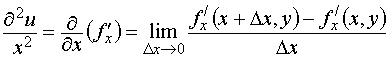
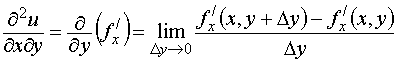
Обозначение производных второго порядка:

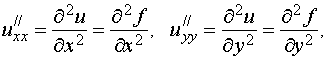
Последние две производные называются смешанными.

Теорема 11.13 (Шварца). Если смешанные частные производные

второго порядка непрерывны, то они равны между собой. Другими

словами, результат смешанного дифференцирования не зависит от порядка.

Теорема (о равенстве смешанных производных):

Пусть имеем функцию f (х, у). Если в окрестности точки M0 (x0, y0) существуют смешанные производные и , непрерывные в точке M0, то они в этой точке равны. То есть = .

Замечание. Утверждение теоремы справедливо для смешанных производных любого порядка по любым переменным, лишь бы число дифференцирования по каждой переменной было одно и то же.

35) Дифференциалы высших порядков

Полный дифференциал d z функции нескольких переменных есть, в свою очередь, функция тех же переменных и мы можем определить полный дифференциал этой последней функции. Например:

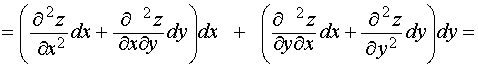
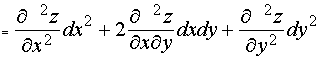
Вычисляя точно так же дифференциал третьего порядка d3z (считая и постоянными), мы получим:

Эти выражения приводят нас к следующей символической формуле для дифференциала любого порядка в случае, когда переменные независимые:

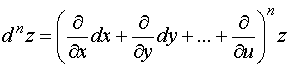
Если же d х и d у нельзя считать постоянными, то эта формула уже не будет справедлива. Действительно:

Формула Тейлора для дифференциалов высших порядков

36)Экстремум функции двух переменных

Рассмотрим функцию z = f{x,y) двух переменных, определенную в некоторой области D.

Функция f(x;y) имеет строгий локальный максимум (минимум) в точке Мо(хо;yо), если неравенство f(xo;yo)>f(x;y) (f (хо;yо) < f(x;y)) имеет место во всех точках М(х;у) =/ Мо из некоторой достаточно малой окрестности точки Мо.

Вопрос определения экстремумов (максимумов или минимумов) в некоторых случаях решается просто, если /(х; у) дифференцируемая функция в окрестности точек экстремума.

Теорема 11.18 (необходимые условия экстремума). Если f(x;y) дифференцируема в точке (xо;yо) и имеет экстремум в этой точке, то ее дифференциал равен нулю:

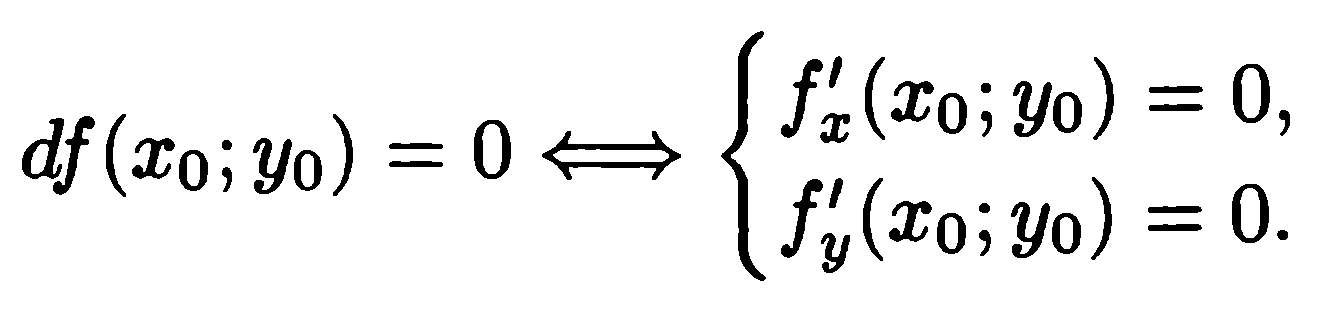
Т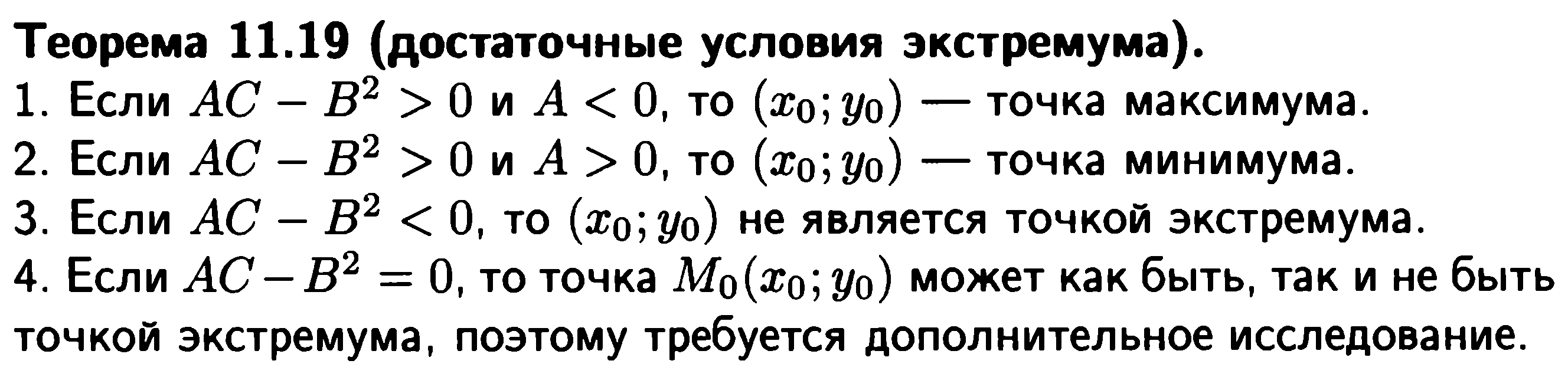 очка (хо;уо) называется стационарной точкой функции f(x;у), если df(xo;yo) = 0.

Экстремум функции в области

Речь идет о нахождении наибольшего и (или) наименьшего значения данной функции z — f(x;y) в замкнутой области D. Для этого следует найти сначала все локальные экстремумы внутри области D, а затем также наибольшее и наименьшее значения на ее границе сигмаD. В результате сравниваем полученные величины, и задача завершена.

Добавим, что как правило, граница сигмаD состоит из совокупности отдельных участков, на каждом из которых задача сводится к исследованию на экстремум функции одной переменной z = Фиi{t), где i — номер участка, a t — независимая переменная на этом участке, которая может совпасть с х или у или быть отдельным параметром.

3 7) частные производные от z=f(x;y) по двум частным направлениям осей Ox и Oy.

П усть l – некоторое направление(вектор с началом в точке Мо), a e=(cosa;sina)—орт этого направления. Пусть М(x0+delta(дальше д)x;y0+дy)—точка в направлении l от Мо. Обозначим дp= . Тогда cosa= ; sina= .

Теорема 11.14. Производная по направлению, касательному к линии уровня поверхности z = f(x;y), равна нулю.

Случай нескольких переменных

По аналогии со случаем функции двух переменных можно определить производную по направлению для функции трех переменных u = f(x;y;z). Окончательная формула такова:

где ё = (cos a; cosb; cosc) — орт направления l или cos a, cosb, cosc — направляющие косинусы направления l.

Теорема 11.15. Производная по направлению, касательному к поверхности уровня функции u = f(x;y,z), равна нулю.

Градиент

Градиентом функции z = f(x;y) (скалярного поля) называется вектор с координатами

Теорема 11.16. Имеет место равенство т.е. производная по направлению l равна скалярному произведению векторов градиента и орта направления l.