21. Правило Лопиталя:

Правило Бернулли-Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и  . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

Точная формулировка

Условия:

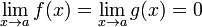1.  или  ;

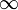2.  и   дифференцируемы в проколотой окрестности  ;

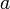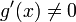3.  в проколотой окрестности  ;

4. существует  ,

тогда существует  .

Пределы также могут быть односторонними.

Доказательство Отношение бесконечно малых

Докажем теорему для случая, когда пределы функций равны нулю (то есть неопределённость вида  .

Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a, мы можем непрерывным образом их доопределить в этой точке: пусть f(a) =g(a) = 0. Возьмём некоторый x из рассматриваемой полуокрестности и применим к отрезку   теорему Коши. По этой теореме получим:

,

но f(a) = g(a) = 0, поэтому  .

Дальше, записав определение предела отношения производных и обозначив последний через A, из полученного равенства выводим:

для конечного предела и

для бесконечного,

что является определением предела отношения функций.

Отношение бесконечно больших

Докажем теорему для неопределённостей вида  .

Пусть, для начала, предел отношения производных конечен и равен A. Тогда, при стремлении x к a справа, это отношение можно записать как A + α, где α — O(1). Запишем это условие:

.

Зафиксируем t из отрезка   и применим теорему Коши ко всем x из отрезка  :

, что можно привести к следующему виду:

.

Д ля x, достаточно близких к a, выражение имеет смысл; предел первого множителя правой части равен единице (так как f(t) и g(t) — константы, а f(x) и g(x) стремятся к бесконечности). Значит, этот множитель равен 1 + β, где β — бесконечно малая функция при стремлении x к a справа. Выпишем определение этого факта, используя то же значение ε, что и в определении для α:

Получили, что отношение функций представимо в виде (1 + β)(A + α), и 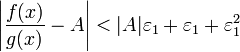 . По любому данному ε можно найти такое ε₁, чтобы модуль разности отношения функций и A был меньше ε, значит, предел отношения функций действительно равен A.

Если же предел A бесконечен (допустим, он равен плюс бесконечности), то

.

В определении β будем брать  ; первый множитель правой части будет больше 1/2 при x, достаточно близких к a, а тогда  .

Для других баз доказательства аналогичны приведённым.

22. Формула Тейлора с остаточным членом в форме Пеано:

РядТе́йлора — разложение функции в бесконечную сумму степенных функций.

Определение

Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a. Формальный ряд

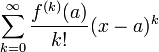
называется рядом Тейлора функции f в точке a.

Формула Тейлора — Пеано Пусть  , z₀ — предельная точка множества D_f и  . Если функция f n-дифференцируема в смысле Ферма — Лагранжа в точкеz₀, то справедлива формула Тейлора — Пеано

где ε_n(z) - непрерывная в точке z₀ функция и ε_n(z₀)=0. Применим метод математической индукции. Если n=0, то утверждение очевидно при ε_n (z)=f(z)-f(z₀). Предположим, что утверждение теоремы справедливо после замены n на n-1 и что функция f n-дифференцируема в смысле Ферма-Лагранжа в точке z₀. Согласно определению, существует такая n-1 дифференцируемая в смысле Ферма-Лагранжа в точке z₀ функция φ, что ∀z∈D_f,

f(z) − f(z₀) = (z − z₀)φ(z)(2)

По предположению

где ε_{n − 1}(z) - непрерывная в точке z₀ функция и ε_{n − 1}(z₀) = 0. Из равенств (2) и (3) получаем:

Что равносильно формуле (1) при ε_n = ε_{n – 1.}