1)

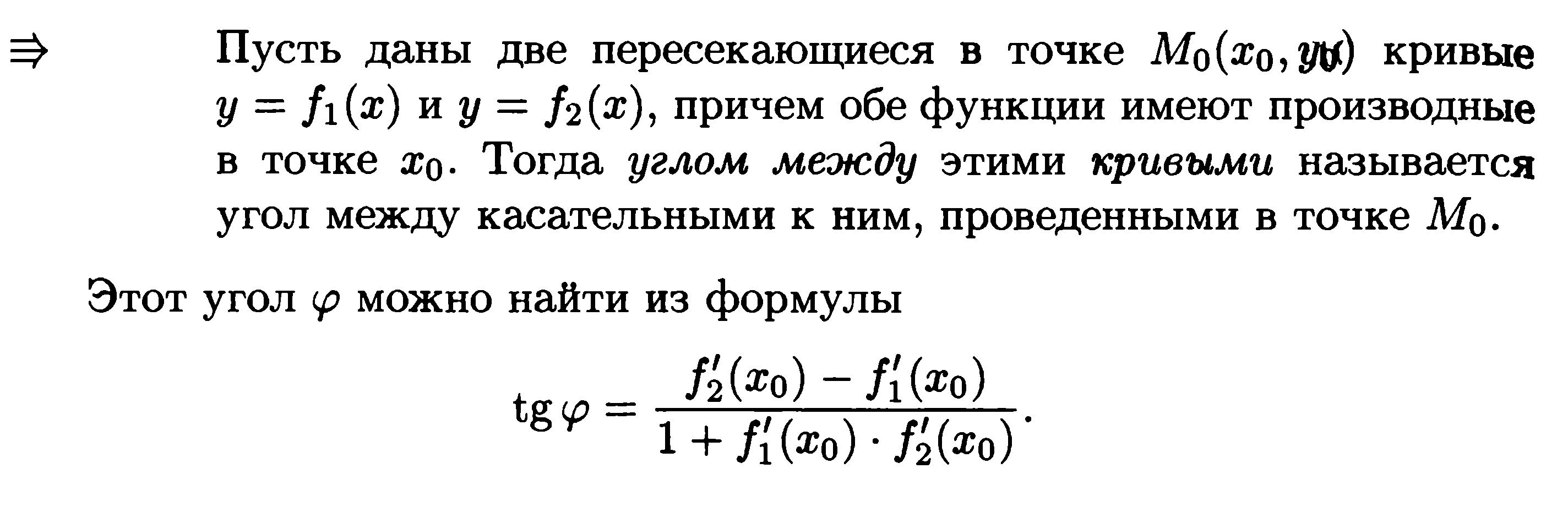
Скорость изменения функции

Пусть s = s(t) — закон прямолинейного движения. Тогда v(t₀) = s'(t₀) выражает мгновенную скорость движения в момент времени t₀. Вторая производная a(t₀) = s''(t₀) выражает мгновенное ускорение в момент времени t₀.

Вообще производная функции y = f(x) в точке x₀ выражает скорость изменения функции в точке x₀, то есть скорость протекания процесса, описанного зависимостью y = f(x).

2 )

3 )

Производная сложной функции

Пусть y – сложная функция x, т.е. y = f(u), u = g(x), или

               (11)

Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция (11) также дифференцируема в точке x и находится по формуле

            (12)

Соотношение (12) часто записывают в виде формулы

                          (13)

справедливой при всех тех значениях x, для которых выполнены условия правила дифференцирования сложной функции.

Замечание. В случае сложной функции y = f(u), u = g(x) аргумент u функции y называют промежуточным аргументом в отличие от независимой переменной x. Тогда правило (13) можно сформулировать так: производная сложной функции равна произведению производной этой функции по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной x.

Для сложной степенной функции

где u  - дифференцируемая функция аргумента x, а n – целое положительное число, формула (4) производной степенной функции на основании правила (13) примет вид

                      (14)

4 )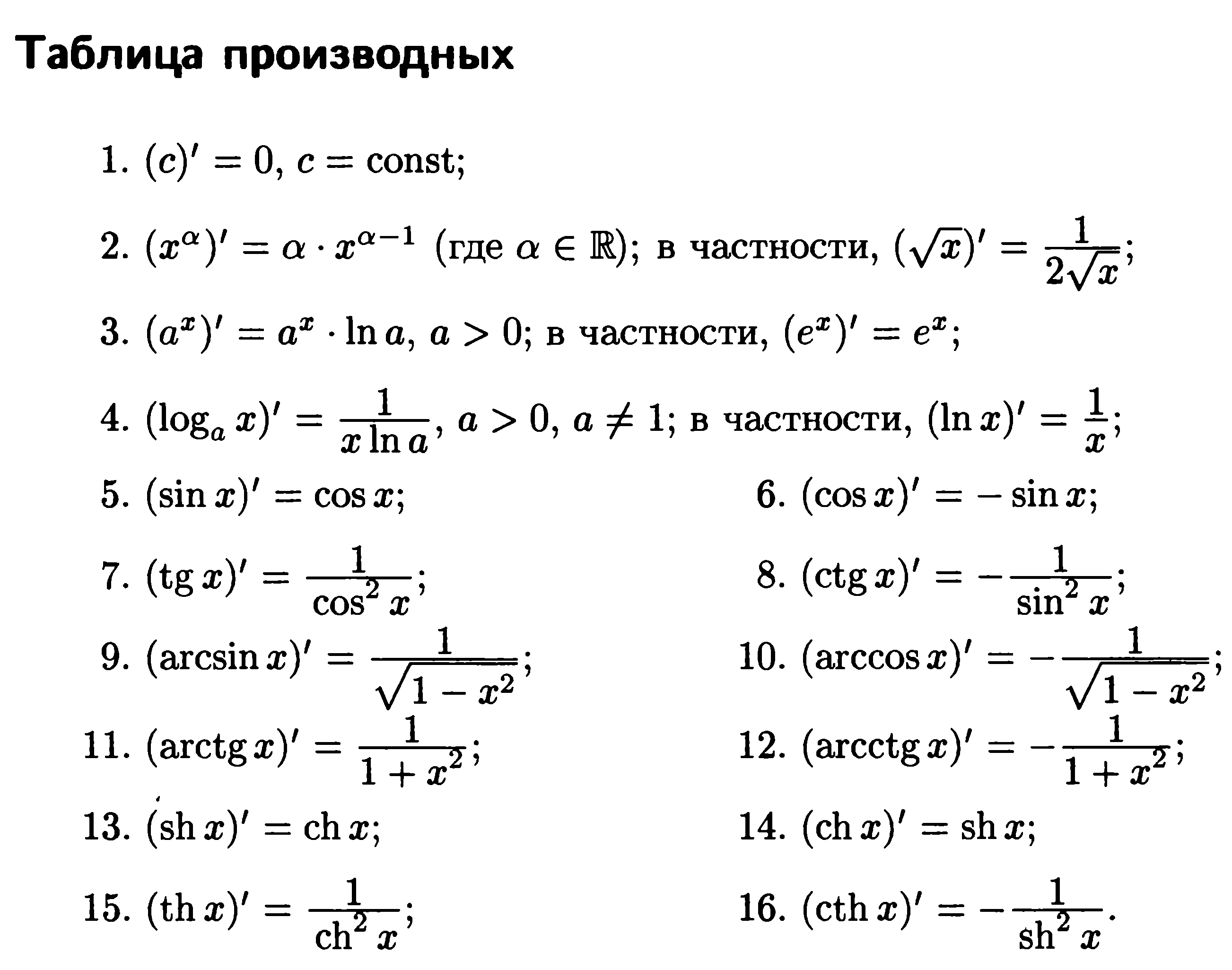

5)

6)

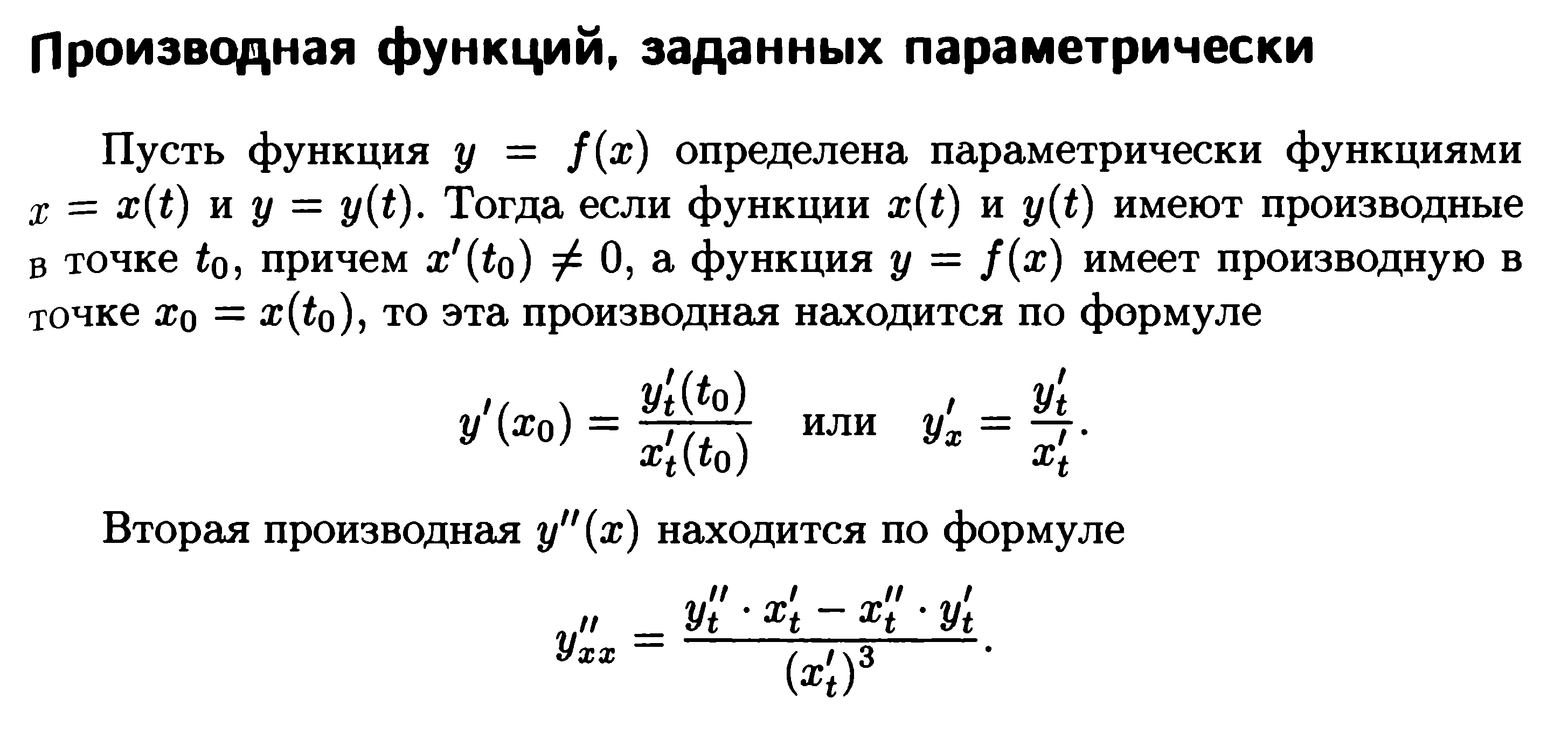
7)

P.S : Разберите, для доказательства этой теории любой пример из головы. Просто решите.

8)Уравнение касательной и нормали к графику функции в точке

Уравнение касательной

Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной:

y/(x)=limΔx→0ΔxΔy

Δy=f(x+Δx)−f(x).  Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k Т.к. x0 и f(x0)∈  прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или

y=f/(x0)·x+f(x0)−f/(x0)·x0. 

 

 

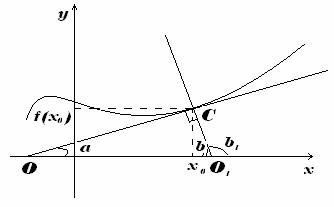
Уравнение нормали

Нормаль-- это перпендикуляр к касательной (см. рисунок). Исходя из этого:

tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)

Т.к. угол наклона нормали -- это угол β1, то имеем:

tgβ1=tg(π−β)=−tgβ=−1f/(x).

Точка (x0,f(x0))∈  нормали, уравнение примет вид:

y−f(x0)=−1f/(x0)(x−x0).

( ссыль.На нормальный вид - http://www.fizmatik.ru/index.php?option=com_content&view=article&id=19&Itemid=20)

9)

Формула Лейбница для n-ой производной произведения двух функций — обобщение правила дифференцирования произведения двух функций на случай n-кратного дифференцирования.

Пусть функции f и g — n раз дифференцируемые функции, тогда

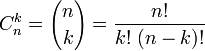где — биномиальные коэффициенты.