2. Меры связи, для данных, измеряемых в различных шкалах

Существуют меры связи, применимые к переменным, оцениваемых не количественно, как прибыль, объем выпускаемой продукции, затраты ресурсов и др., а оцениваемых в других шкалах. В частности, мы рассмотрим коэффициенты корреляции, применяемые для дихотомических (0, 1) данных, данных ранжирования (1,2,…n) и прочих.

Различают четыре типа измерений переменных:

1. Измерения в дихотомической шкале наименований. Фиксируется просто наличие или отсутствие чего-либо. Данные представляют собой нули и единицы. Порядок оценивания является, как правило, произвольным. Примеры: республиканец(1) – демократ – (0); учащийся школы (1) – не учащийся школы (0); мужчина (1) – женщина (0); женат (1) – холост (0).

2. Измерения в дихотомической шкале наименований в предположении нормального распределения. Предполагается, что более утонченные, более полные и более совершенные методы измерения могли бы обеспечить приблизительно нормальное распределение результатов, но рассматриваемые данные говорят лишь о том, будет ли объект занимать положение выше (1) или ниже (0) некоторой точки в этом нормальном распределении. Если в отношении большой группы учащихся было известно только, превышает ли коэффициент интеллекта отметку 120 (обозначим этот факт единицей) или нет (обозначим это 0), то единицы и нули представляли бы собой дихотомические данные, основанные на нормальном распределении. Конечно, было бы неэффективным пренебрегать исходными данными и записывать вместо них единицы и нули, и это, как правило, не делается (несмотря на то, что в ранней истории факторного анализа это было бы удобным с точки зрения вычисления).

3. Измерения в шкале порядка. Данные представляют собой последовательные несвязанные ранги 1, 2, …, n. Эти ранги можно присвоить измерениям другой шкалы (например, когда исходные данные 136, 124, 97 ранжируются номерами 1, 2, 3), или они могут быть прямым переводом восприятий в числа (например, когда судья ранжирует 10 конкурентов от наиболее опытного – 1 до наименее опытного – 10).

4. Измерения в шкалах интервалов или отношений. Существует единица измерения, например дюйм, день и т.д., а (в случае шкалы отношений) нулевая точка на шкале соответствует отсутствию (нулю) измеряемой переменной. Результатом может быть любое единственное число, а разности между отметками отражают разности значений характеристики.

Если измерения можно произвести на уровне шкал интервалов или отношений, то результаты можно преобразовать в любую из трех других названных шкал.

Там, где присутствуют два множества значений и для объектов, и можно измерить любым из четырех возможных способов, т.е. существует 16 возможных пар измерений для двух переменных, которые могут коррелировать. Достаточно рассмотреть 10 из 16 возможных пар, что представлено в таблице 3.3.

Таблица 3.3

Возможные варианты анализа корреляции данных

Шкалы переменной	Шкала переменной
	Дихотомия	Дихотомия, основанная на нормальном распределении	Шкала порядка	Шкала интервалов или отношений
Дихотомия	A	(B)	(C)	(D)
Дихотомия, основанная на нормальном распределении	B	E	(F)	(G)
Шкала порядка	C	F	H	(I)
Шкала интервалов или отношений	D	G	I	J

Случай А

Обе переменные измеряются в дихотомических шкалах наименований: мера связи коэффициент :

,

где и - доля переменных, имеющих единицу по признаку или по признаку соответственно; и - доля переменных, имеющих нуль по или по соответственно, которая равна ; - доля переменных, которые имеют единицу как по так и по .

Рассмотрим пример вычисления коэффициента в среде MS Excel. Предположим, что необходимо определить взаимосвязь между наличием у предприятий конкурентов и размером их бизнеса. На рис. 3.6 приведена копия экрана с входными данными и результатами расчетов. На рис. 3.7 приведена копия экрана с расчетными формулами.

Видно, что для подсчета количества признаков, имеющих одновременно значения 1 или 0, в используется функция вида: ЕСЛИ(И(B2=1;C2=1);B2;0). Коэффициент рассчитывается с использованием стандартных математических функций: (F4-E2*E3)/КОРЕНЬ(E2*G2*E3*G3). Однако данный коэффициент можно получить и с помощью встроенной статистической функции, которая была рассмотрена ранее: КОРРЕЛ(B2:B13;C2:C13).

Проанализировав полученные данные (коэффициент ), можно сделать выводы, что имеется слабая корреляционная связь, т.е. независимо от уровня бизнеса конкуренция у предприятий все равно существует.

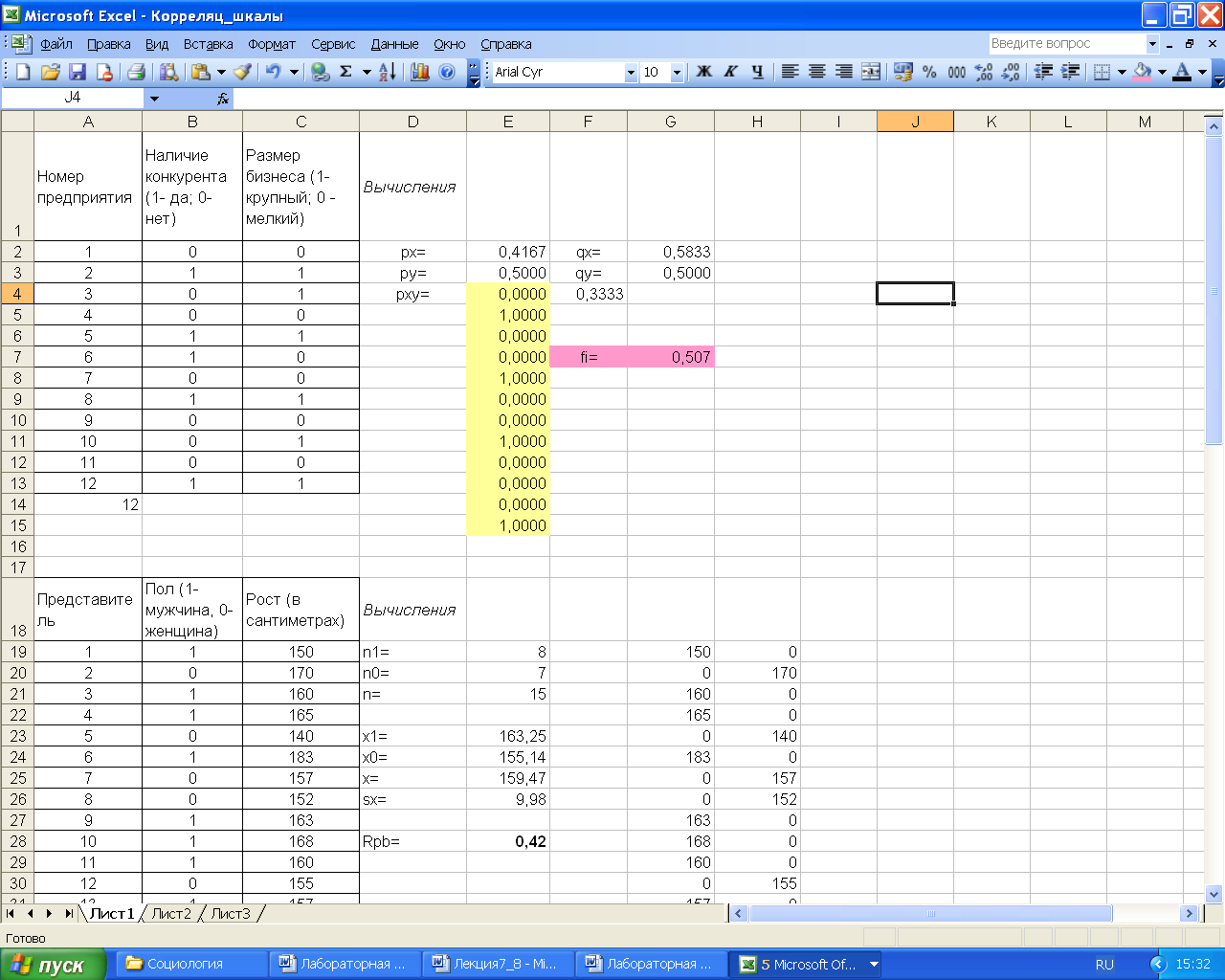
Рис. 3.7 - Исходные данные и результаты расчета коэффициента

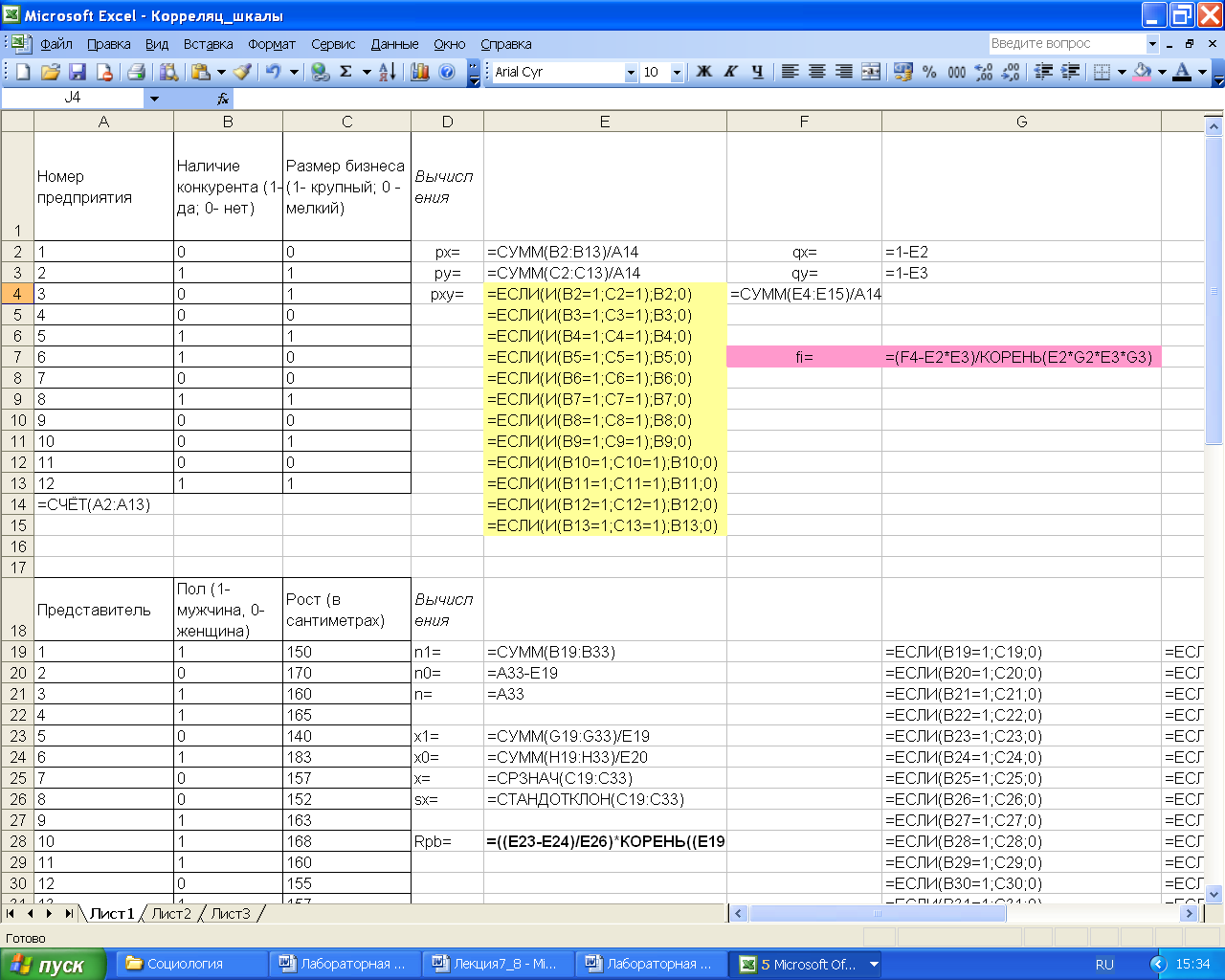
Рис. 3.8 – Расчетные формулы для вычисления коэффициента

Случай В

- дихотомический признак; - тоже дихотомический, но основан на нормальном распределении. Нет коэффициента для измерения меры связи!

Случай С

- дихотомический признак; - порядковый. Для этого случая используется бисериальный ранговый коэффициент корреляции, который будет рассмотрен позднее.

Случай D

- дихотомический признак; - измеряется в шкале интервалов или отношений: мера – точечно-бисериальный коэффициент корреляции.

Термин бисериальный относится к тому обстоятельству, что существуют две серии объектов при наблюдении : те что имеют нуль по , и те что имеют единицу. Коэффициент рассчитывается следующим образом:

,

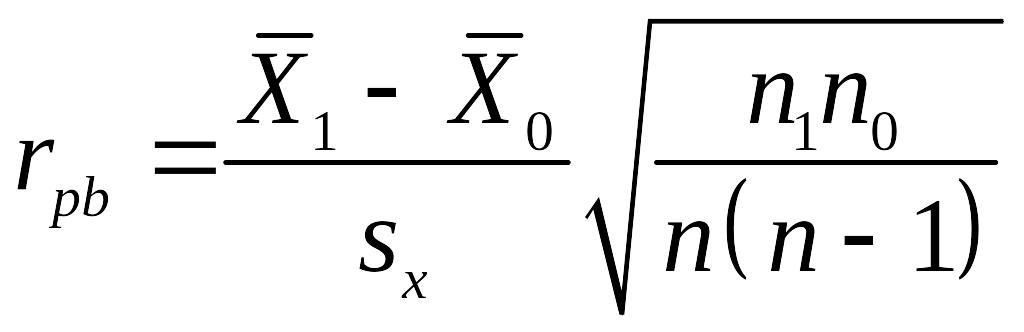где - среднее по объектов, имеющих единицы по ; - среднее по объектов, имеющих нуль по ; - стандартное отклонение всех значений по ; - число объектов, имеющих единицу по ; - число объектов, имеющих нуль по ; .

Рассмотрим вычисление точечно-бисериального коэффициента корреляции с помощью электронных таблиц MS Excel. Пусть необходимо определить связь уровня квалификации рабочих с их производительностью. На рис. 3.9 приведены исходные данные по уровню квалификации и объемам выработки деталей в сутки, а также результаты расчетов точечно-бисериального коэффициента. На рис. 3.10 – расчетные формулы.

Видно, что для подсчета количества признаков, имеющих значения 1 или 0 используются функции вида: ЕСЛИ(B19=1;C19;0) и ЕСЛИ(B19=0;C19;0). Для определения среднего значения и расчета дисперсии были выбраны стандартные статистические функции СРЗНАЧ(C19:C33) и СТАНДОТКЛОН(C19:C33) соответственно. Вычисление коэффициента выполнялся с использованием математических функций: ((E23-E24)/E26)*КОРЕНЬ((E19*E20)/(E21*(E21-1))). Однако такие же данные можно получить и при помощи стандартной функции КОРРЕЛ(B19:B33;C19:C33).

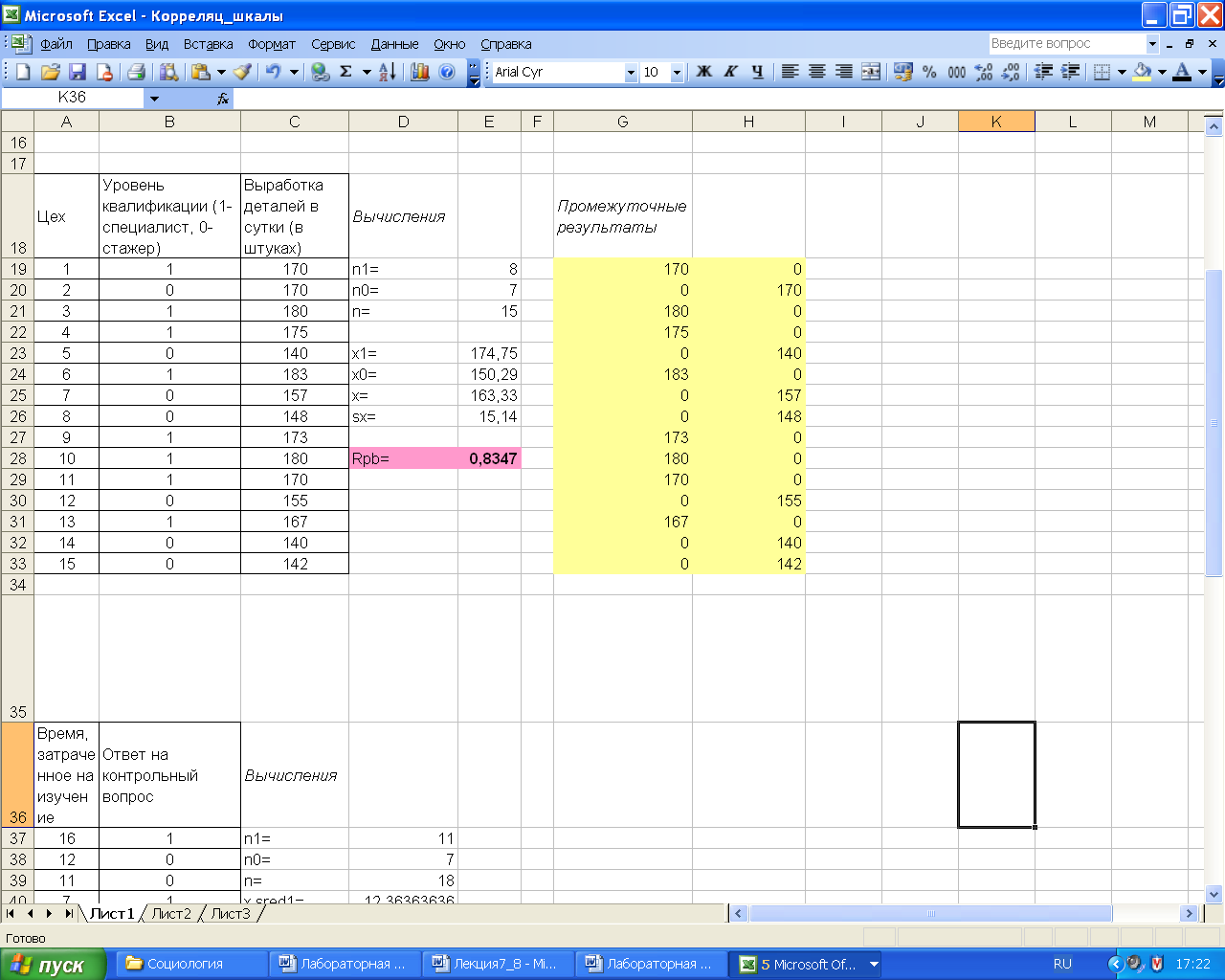
Рис. 3.9 - Исходные данные и результаты расчета коэффициента

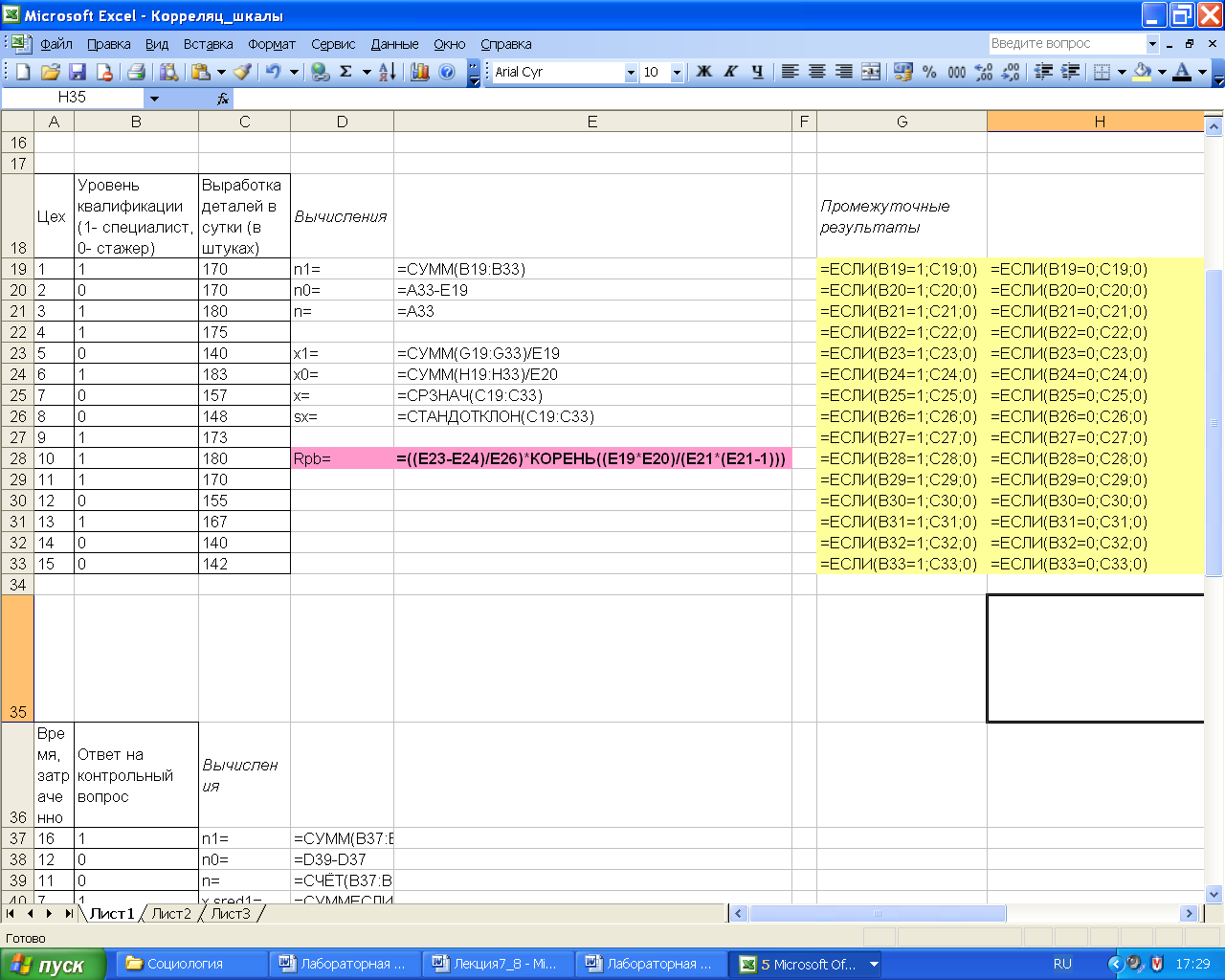
Рис. 3.10 – Расчетные формулы для вычисления коэффициента

Случай Е

Обе переменные дихотомические, основанные на нормальных распределениях: мера – тетрахорический коэффициент корреляции, который в общем случае может быть заменен коэффициентом .

Случай F

- дихотомический признак, основанный на нормальном распределении; - порядковый. Нет коэффициента, подходящего для описания связи между переменными, измеряемыми таким образом.

Случай G

- дихотомический признак, основанный на нормальном распределении; - измеряется в шкале интервалов или отношений (или наоборот): мера – бисериальный коэффициент корреляции _{, который рассчитывается следующим образом:}

где - среднее по объектов, имеющих единицы по ; - среднее по объектов, имеющих нуль по ; - стандартное отклонение всех значений по ; - число объектов, имеющих единицу по ; - число объектов, имеющих нуль по ; ; - ордината (т.е. высота) нормированного нормального распределения в точке, за которой лежит процентов площади под кривой.

В отличие от других коэффициентов корреляции, коэффициент _{иногда может принимать значения ниже –1 и выше +1. Но это означает, что не корректно предположение о нормальности распределения , либо анализируется выборка с малым значение (например, ).}

Пример вычисления бисериального коэффициента корреляции приведен на рис. 3.11. С помощью данного коэффициента можно, например, установить связь между временем, потраченным на изготовление детали и уровнем квалификации рабочего.

Расчетные формулы представлены на рис. 3.12.

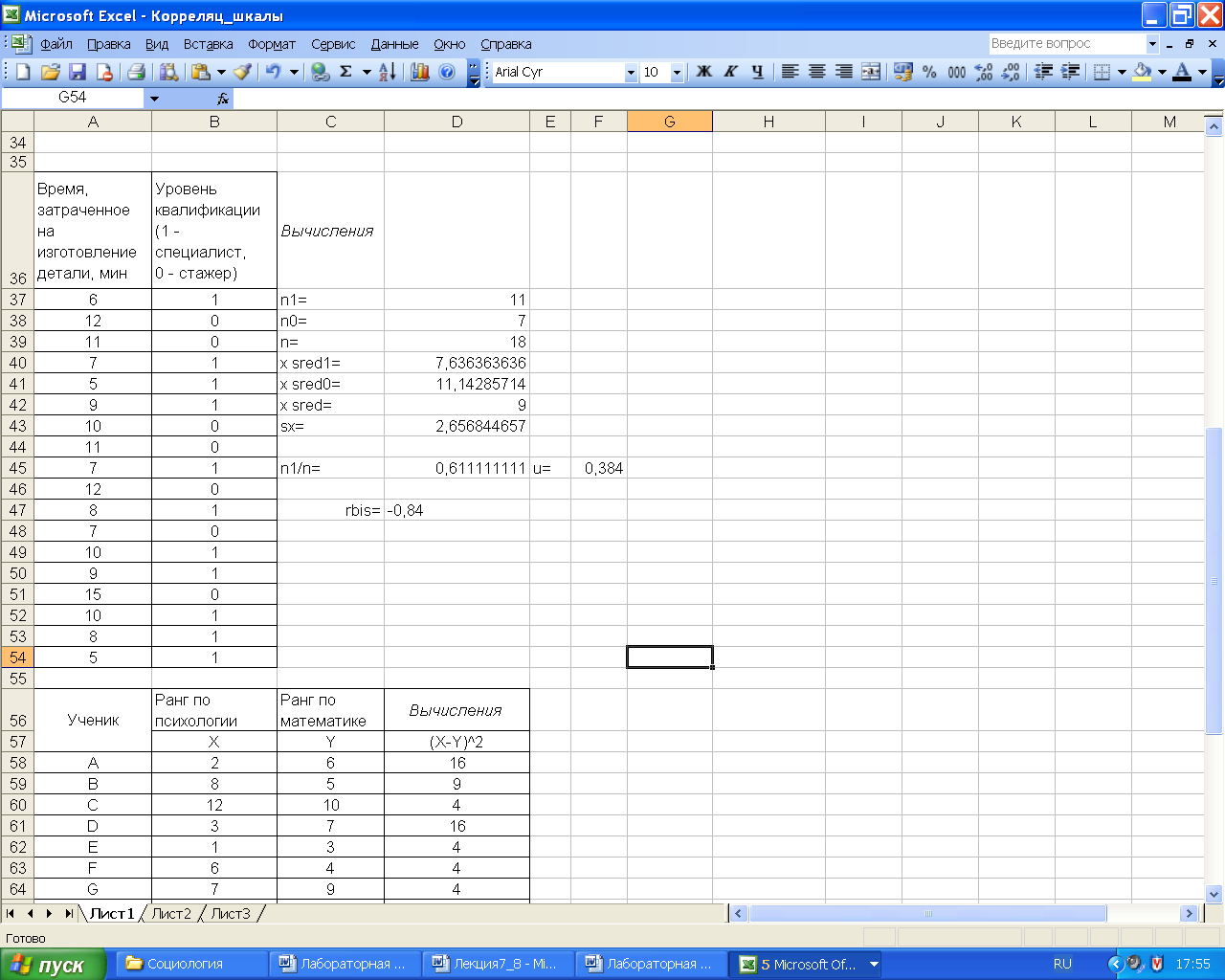
Рис. 3.11 – Исходные данные и результаты вычисления коэффициента

Рис. 3.12 – Расчетные формулы для вычисления коэффициента

_{На основе анализа полученных результатов можно сделать вывод, что имеется отрицательная корреляционная связь между рассматриваемыми переменными, т.е. чем меньше времени потрачено на изготовление детали, тем выше квалификация работника.}

_{Случай Н}

Обе переменные измеряются в шкалах порядка. Мера – коэффициент ранговой корреляции Спирмена.

Коэффициент корреляции рангов Спирмена ( ) — это непараметрический показатель, с помощью которого пытаются выявить связь между рангами соответственных величин в двух рядах измерений.

Этот коэффициент рассчитывать проще, однако результаты получаются менее точными, чем при использовании коэффициента корреляции . Это связано с тем, что при вычислении коэффициента Спирмена используют порядок следования данных, а не их количественные характеристики и интервалы между классами.

Дело в том, что при использовании коэффициента ранговой корреляции Спирмена ( ) проверяют только, будет ли ранжирование данных для какой-либо выборки таким же, как и в ряду других данных для этой выборки, попарно связанных с первыми (например, будут ли одинаково «ранжироваться» предприятия при проверки их налоговым инспектором и аудиторской фирмой, или даже при проверке их двумя разными инспекторами?). Если коэффициент близок к +1, то это означает, что оба ряда практически совпадают, а если этот коэффициент близок к -1, можно говорить о полной обратной зависимости.

Коэффициент вычисляют по формуле

где - разность между рангами сопряженных значений признаков и (независимо от знака).

Пример вычисления коэффициента ранговой корреляции Спирмена для определения связи между проверками различных служб финансового положения предприятий одного города приведен на рис. 3.13. Расчетные формулы приведены на рис. 3.14. Аналогичный результат можно получить и с помощью встроенной функции КОРРЕЛ(B58:B69;C58:C69).

Анализируя полученные данные можно сделать вывод, что ранги, присвоенные налоговой и аудиторскими фирмами финансовому состоянию предприятий коррелируются между собой.

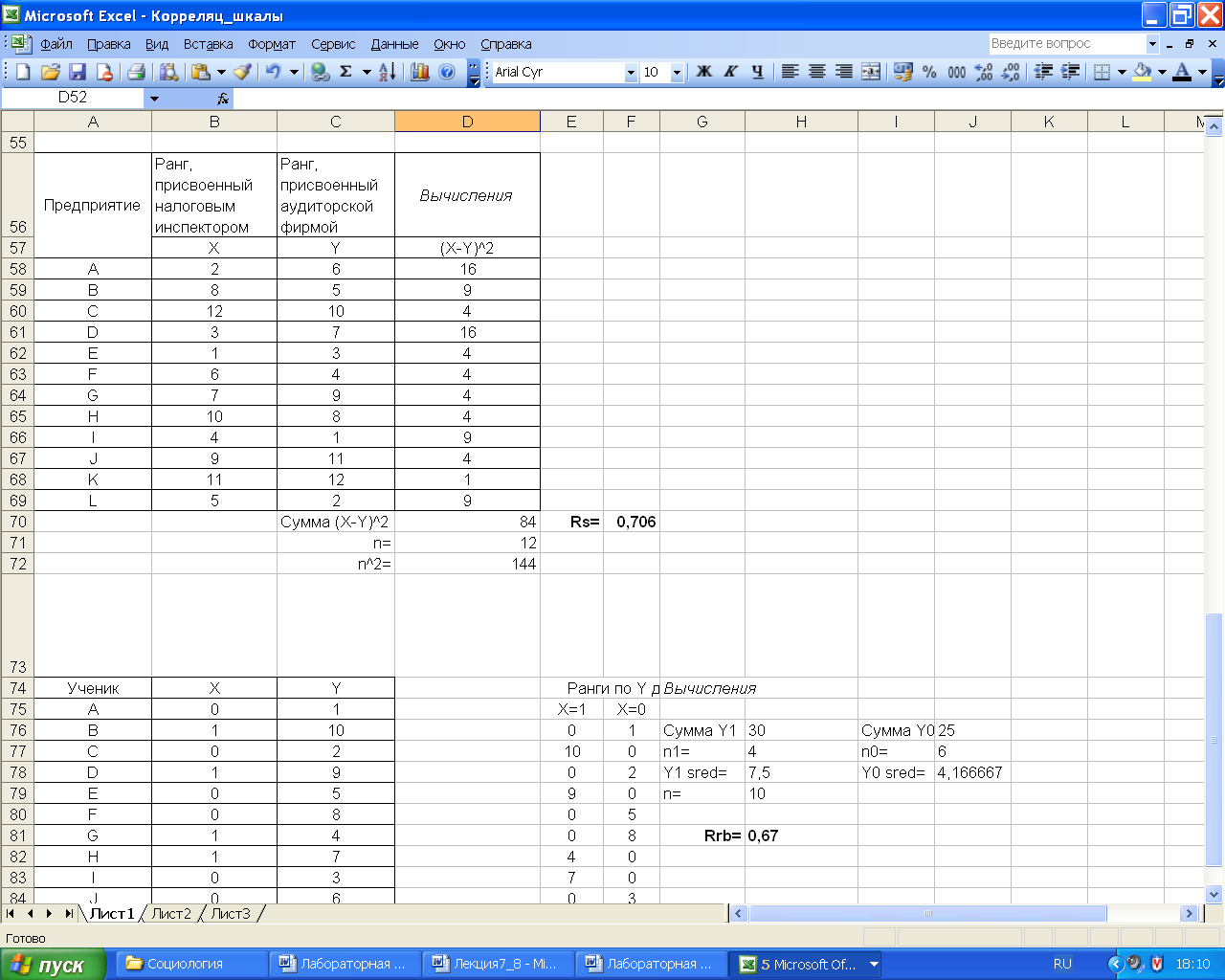
Рис. 3.13 – Исходные данные и результаты вычисления коэффициента Спирмена

Рис. 3.14 – Расчетные формулы для вычисления коэффициента Спирмена

Обычно этот непараметрический тест используется в тех случаях, когда нужно сделать какие-то выводы не столько об интервалах между данными, сколько об их рангах, а также тогда, когда кривые распределения слишком асимметричны и не позволяют использовать такие параметрические критерии, как коэффициент (в этих случаях бывает необходимо превратить количественные данные в порядковые).

Связанные ранги

В измерениях часто имеют место связанные ранги. В таких случаях действует особое правило приписывания рангов. Например, если 12-й и 13-й ученик будут иметь одинаковый средний балл 4,5, то обоим надо присвоить ранг, равный среднему двух рангов (12+13)/2=12,5.

Когда имеют место связанные ранги, уравнение для расчета , приведенное выше не может быть использовано. Тогда применяется либо уравнение для расчета коэффициента корреляции или, если связанных рангов не много, использовать формулу для расчета , но полученное значение будет приближенное.

Случай I

- измеряется в шкале порядка, - в шкале интервалов или отношений. Для этого частного случая не было разработано и исследовано никакого коэффициента. Если будет иметь место такой случай, то целесообразно преобразовать оценки в ранги и найти коэффициенты ранговой корреляции Спирмена или Кенделла.

Случай С

Пусть - дихотомическая переменная, а - переменная, имеющая несвязанных рангов 1, 2, … . Тогда, коэффициент, определяющий связь между признаками, измеряемых в таких шкалах – коэффициент биссериальной ранговой корреляции:

,

где - средний ранг объектов, имеющих 1 по ; а - средний ранг объектов с 0 по .

Этот коэффициент используется, например, тогда, когда необходимо установить связь между размером предприятия и, присвоенным ему, рангом. Пример расчета коэффициента биссериальной ранговой корреляции приведен на рис. 3.15. Расчетные формулы на рис. 3.16.

Рис. 3.15 - Исходные данные и результаты вычисления коэффициента биссериальной ранговой корреляции

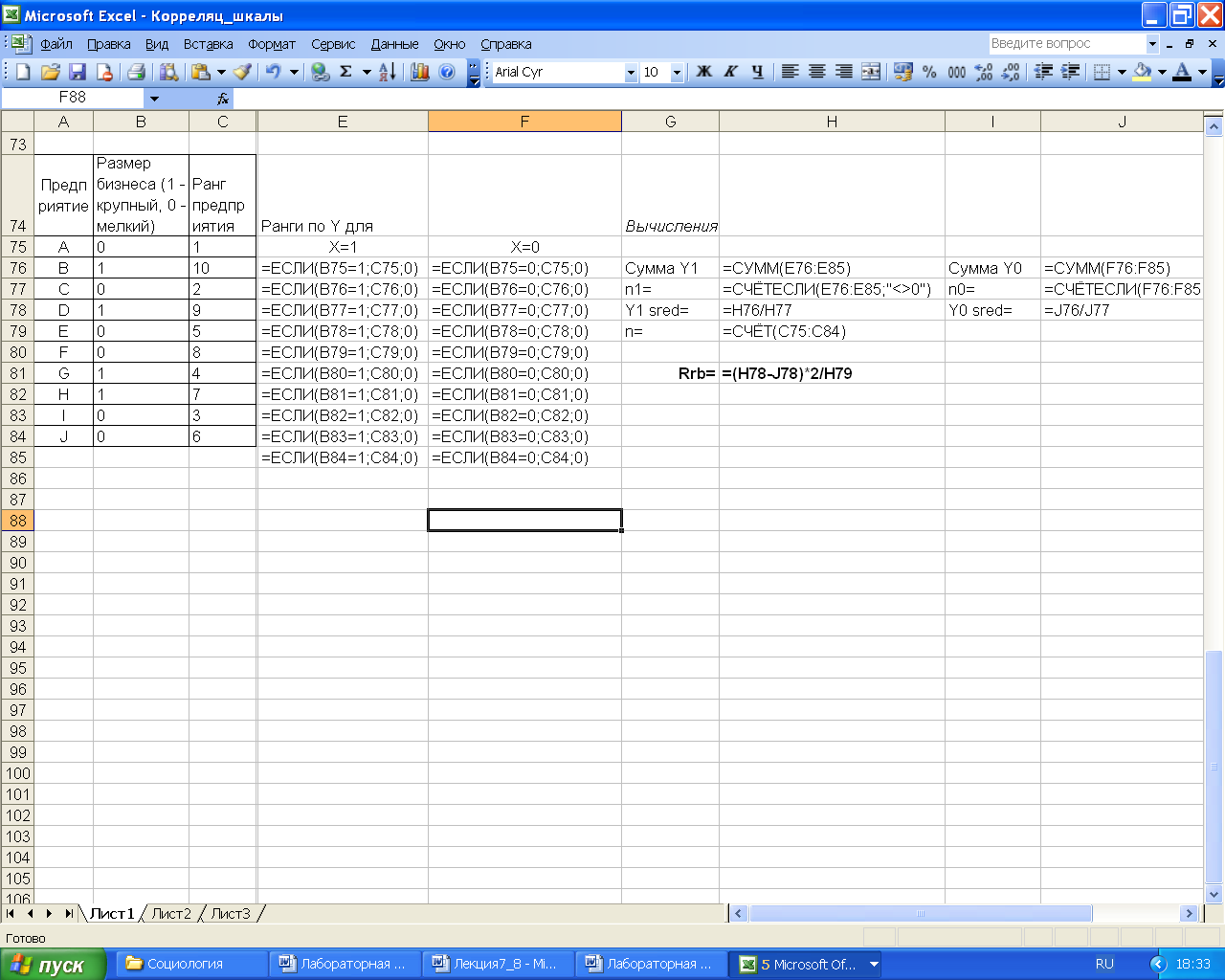
Рис. 3.16 - Расчетные формулы для вычисления коэффициента биссериальной ранговой корреляции

Для расчета рангов и подсчета количества рангов используются следующие функции: ЕСЛИ(B75=1;C75;0), ЕСЛИ(B75=0;C75;0) и СЧЁТЕСЛИ(E76:E85;"<>0").

Анализируя полученные результаты можно сделать выводы, что связь между рассматриваемыми переменными существует.