Тоді за теоремами множення і додавання ймовірностей маємо

.

Отже, .

5*. Ймовірність появи хоча б однієї події

Нехай маємо незалежних в сукупності подій і нехай ймовірності цих подій відомі. Необхідно знайти ймовірність появи хоча б однієї події.

Відповідь на це дає наступна теорема.

Теорема. Ймовірність появи хоча б однієї з незалежних в сукупності подій дорівнює різниці між одиницею і добутком ймовірностей протилежних подій.

(2)

Доведення. Позначимо через – події ; .

.

, ;

.

Якщо , , то

(2')

Приклад 17. На підстанції є три блоки приладів. Ймовірність того, що на протязі зміни перший блок не потребує уваги – ; другий – ; третій – . Знайти ймовірність того, що хоча б один блок уваги диспетчера.

Розв’язання.

– подія, блок потребує уваги.

– потребує уваги один прилад.

– потребує уваги два прилади.

– потребує уваги три прилади.

.

6*. Теорема додавання ймовірностей сумісних подій

Якщо події несумісні, то

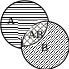
Дві події називаються сумісними, якщо поява однієї з них не виключає появи другої в однім і тим же випробуванні.

Якщо події і сумісні, то справедлива наступна теорема.

Теорема. Ймовірність суми двох сумісних подій дорівнює сумі ймовірностей цих подій без ймовірності їх спільного здійснення.

(*)

Доведення. Оскільки події і сумісні за умовою, то подія настане, якщо настане одне із наступних трьох несумісних подій:

, або .

За теоремою додавання ймовірностей несумісних подій

(**)

Подія відбудеться, якщо настане одне з двох несумісних подій: або .

Звідси

()

Аналогічно маємо

()

Підставивши () і () в (* *) отримаємо

Зауваження 1. Якщо події і незалежні, то маємо

.

Якщо події А і В і , то

.

З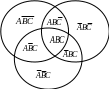 ауваження 2. Зовсім аналогічно записується теорема для суми подій більших двох.

.

Приклад 18. На заводі ведеться вибраковка деталей, якщо вони мають один або два дефекти. Ймовірність появи одного дефекту – ; появи двох дефектів – . Знайти ймовірність вибраковки деталей.

Розв’язання.

; .

.

Приклад 19. Знайти надійність схеми, якщо надійність кожного елементу . Відмови елементів є незалежними.

Розв’язання.

Надійність 1-го ланцюга ;

Надійність 2-го ланцюга

.

Застосувавши теорему додавання сумісних подій отримаємо

.

П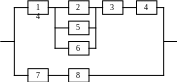 риклад 20. Обчислити надійність схеми, якщо надійність елементів – ; – ; – .

Розв’язання.

;

; ;

.

16