
- •Лекція № 2-3
- •Питання лекції:
- •1*. Теорема додавання ймовірностей несумісних подій
- •2*. Повна група подій. Протилежні події
- •3*. Добуток подій. Умовна ймовірність. Теорема множення сумісних подій
- •Є випадок їх сумісного здійснення , якому сприяє подій.
- •4*. Незалежні події. Теорема множення для незалежних подій. Надійність механізмів, приладів і систем
- •Тоді за теоремами множення і додавання ймовірностей маємо
- •5*. Ймовірність появи хоча б однієї події
- •6*. Теорема додавання ймовірностей сумісних подій
Лекція № 2-3, 3 семестр, ІТП
Лекція № 2-3
Тема: Складання ймовірностей несумісних і сумісних подій. Залежні і незалежні випадкові події. Теореми множення ймовірностей незалежних і залежних подій та слідства з них.
Питання лекції:
Теорема додавання ймовірностей несумісних подій.
Повна група подій. Протилежні події.
Добуток подій. Умовна ймовірність. Теорема множення сумісних подій.
Незалежні події. Теорема множення для незалежних подій. Надійність механізмів, приладів і систем.
Ймовірність появи хоча б однієї події.
Теорема додавання ймовірностей сумісних подій.
1*. Теорема додавання ймовірностей несумісних подій
За формулами класичної, статистичної і геометричної ймовірності не завжди можна обчислити ймовірності випадкових подій. Тому на практиці застосовуються методи, які дозволяють на основі відомих ймовірностей одних подій визначати ймовірності інших подій, пов’язаних з ними. Теорія ймовірностей становить систему таких методів. Самими простими з них є теореми додавання ймовірностей і теореми множення ймовірностей.
Означення
1. Сумою
![]() двох подій
двох подій
![]() і
і
![]() називається подія
називається подія
![]() ,
яка полягає в здійснені події
,
або
,
або обох разом.
,
яка полягає в здійснені події
,
або
,
або обох разом.
Позначається так:
![]() .
.
К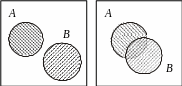 орисною
є геометрична інтерпретація цього
поняття.
орисною
є геометрична інтерпретація цього
поняття.
Нехай подія полягає в тому, що кинута точка попадає в область , а подія полягає в тому, що точка попадає в область , тоді подія полягає в тому, що точка належить замальованій області.
Приклад 1. Проведемо два постріли по мішені. Нехай подія є влучення при першому пострілі. Подія – при другому пострілі, тоді подія є влучення в ціль при першому пострілі або другому пострілі, або при обох.
Аналогічні поняття переносяться для сум великої кількості скінчених подій.
Означення 2. Сумою несумісних подій
![]()
![]() називається подія
,
яка полягає в здійснені хоча б однієї
з цих подій. Тоді
називається подія
,
яка полягає в здійснені хоча б однієї
з цих подій. Тоді
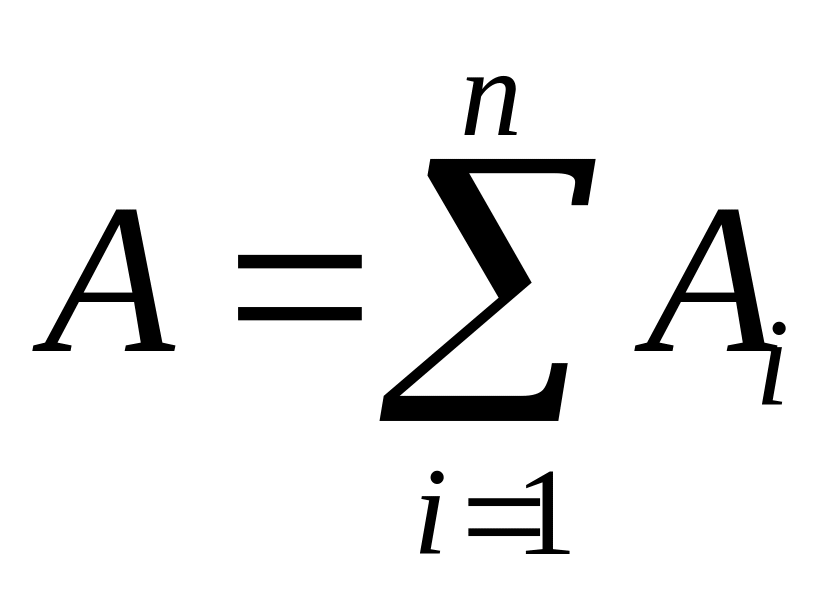 .
.
Приклад 2. Проводиться стрільба по мішені:
![]() –
–
![]() влучень,
влучень,
![]() –
–
![]() влучення,
влучення,
![]() –
–
![]() влучення,
влучення,
![]() –
–
![]() влучення,
влучення,
![]() –
–
![]() влучення,
влучення,
![]() –
–
![]() влучень.
влучень.
![]() – не більше двох влучень.
– не більше двох влучень.
![]() – не менш 4-х влучень.
– не менш 4-х влучень.
Теорема 1. Ймовірність суми двох несумісних подій і дорівнює сумі ймовірностей цих подій, тобто
![]()
Доведення. Нехай
![]() – загальне число можливих елементарних
випробувань,
– загальне число можливих елементарних
випробувань,
![]() – число випробувань сприятливих події
;
– число випробувань сприятливих події
;
![]() – число випробувань сприятливих події
.
– число випробувань сприятливих події
.
Число випробувань сприятливих появі
події
,
або події
,
дорівнює
![]() .
Отже,
.
Отже,
![]()
Прийнявши до уваги, що
![]() ,
,
![]() отримаємо
отримаємо
Геометрична інтерпретація доведення теореми:
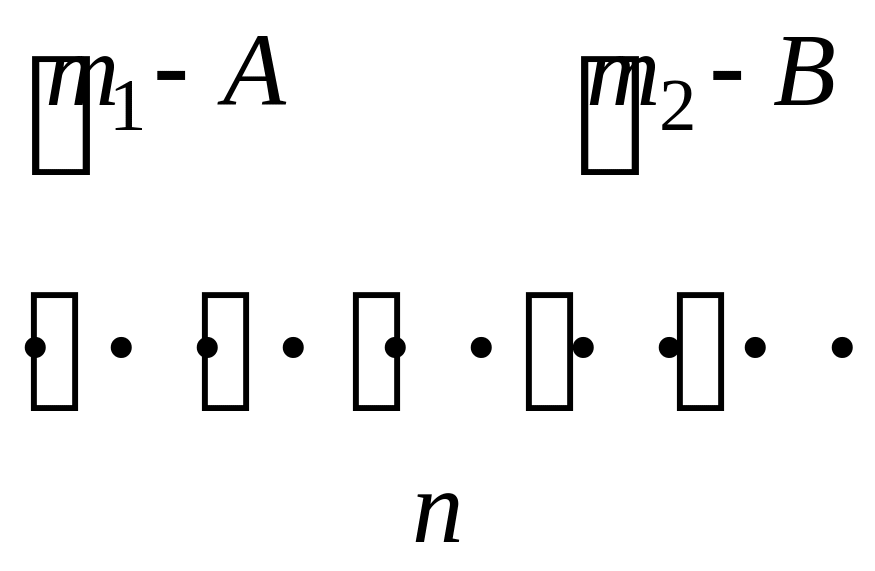
Теорема 2. Ймовірність появи однієї з попарно-несумісних подій , байдуже якої, дорівнює сумі ймовірностей цих подій, тобто
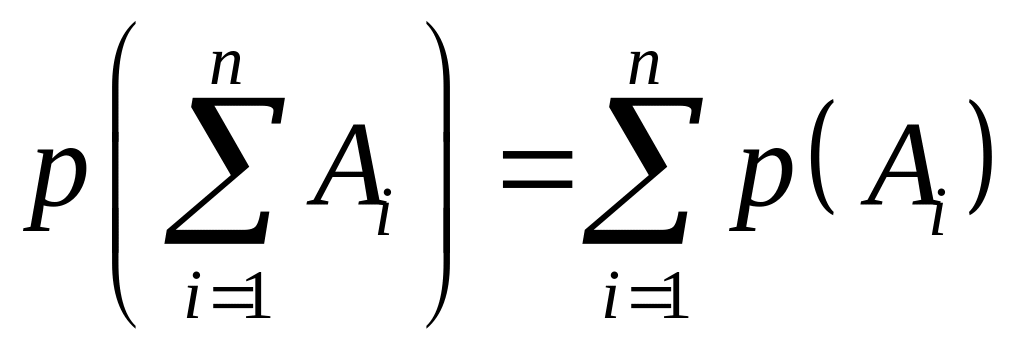 .
.
(Без доведення).
2*. Повна група подій. Протилежні події
Наслідок 1. Якщо події
,
,
...,
![]() утворюють повну групу попарно-несумісних
подій, то
утворюють повну групу попарно-несумісних
подій, то
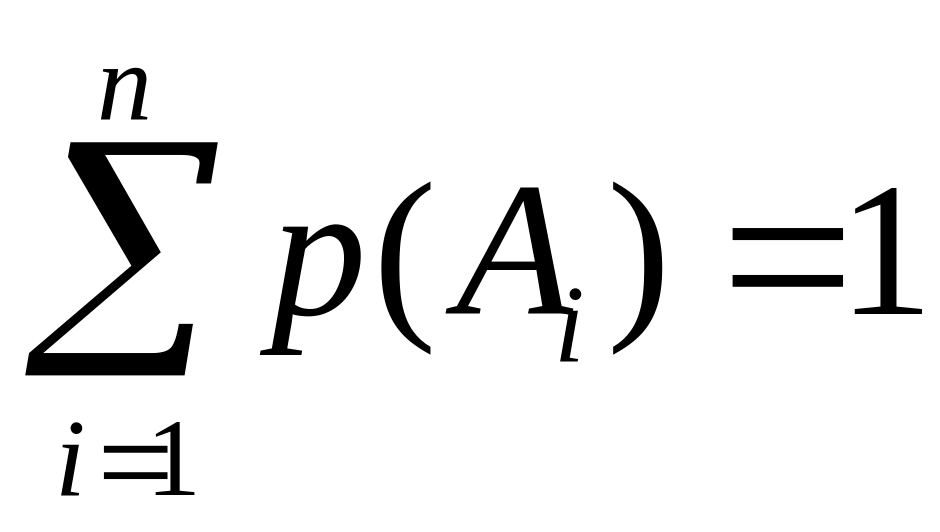 .
.
Означення 3. Дві несумісні події називаються протилежними, якщо вони утворюють повну групу подій.
Подія протилежна події
позначається через
![]() .
.
Приклади: влучення і промах при пострілі, випадання герба і цифри.
Наслідок 2. Сума ймовірностей протилежних подій дорівнює одиниці, тобто
![]() .
.
На практиці ймовірність події
позначають через
![]() ,
а ймовірність протилежної події
– через
,
а ймовірність протилежної події
– через
![]() ,
тобто
,
тобто
![]() ,
,
![]() ,
тоді
,
тоді
![]() і
і
![]() .
.
Приклад 3. Стрілець робить один
постріл по цілі, яка складається з круга
і двох концентричних кілець. Ймовірність
влучення в круг і кільця відповідно
дорівнюють
![]() ;
;
![]() ;
;
![]() .
Обчислити ймовірність влучення в ціль.
.
Обчислити ймовірність влучення в ціль.
Розв’язання. Позначимо через подією, що полягає у влученні в круг, через – влучення в перше кільце, через – влучення в друге кільце. Через – влучення в ціль. Тоді , так як події , і – несумісні, то за теорією додавання ймовірностей, маємо
![]() .
.
Приклад 4. Стрілець зробив один
постріл по мішені. Ймовірність влучення
в десятку дорівнює
![]() ;
в дев’ятку –
;
в вісімку –
;
в дев’ятку –
;
в вісімку –
![]() .
Обчислити ймовірність наступних подій:
– вибито не менше восьми очок, В – вибито
більше восьми очок.
.
Обчислити ймовірність наступних подій:
– вибито не менше восьми очок, В – вибито
більше восьми очок.
Розв’язання. Позначимо через
подію влучення в десятку,
– в дев’ятку,
– в вісімку. Тоді
![]() ;
;
![]() ;
;
![]() .
.
1)
.
Так як події
,
і
– несумісні, то
![]() .
.
2)
![]()
![]() .
.
Приклад 5. В лотереї
![]() білетів, з них
білет виграє
білетів, з них
білет виграє
![]() ,
,
![]() білетів по
білетів по
![]() ,
,
![]() білетів виграють по
білетів виграють по
![]() і
і
![]() білетів по
білетів по
![]() Покупець бере один білет. Чому дорівнює
ймовірність виграти не менше
?
Покупець бере один білет. Чому дорівнює
ймовірність виграти не менше
?
Розв’язання. Позначимо через подію, яка полягає в тому, що виграш становить , через – подію – виграш становить , – подію – виграш становить , –
Через позначимо подію, що виграш не менш , тоді , і так як події , і – несумісні, то
![]() .
.
Приклад 6. В коробці лежать конденсатори
![]() по
по
![]() і
і
![]() по
по
![]() однакових на дотик. Навмання беруть
конденсатори. Обчислити ймовірність
того, що вони одного номіналу.
однакових на дотик. Навмання беруть
конденсатори. Обчислити ймовірність
того, що вони одного номіналу.
Розв’язання. Позначимо через
подію, що конденсатори по
,
а через
подію, що конденсатори по
.
Через
позначимо подію, що вони одного номіналу,
або по
,
або по
,
тобто
![]() .
Так як події несумісні, то
.
Так як події несумісні, то
![]() .
.
![]() – число сприятливих випадків, що
конденсатори будуть по
,
а
– число сприятливих випадків, що
конденсатори будуть по
,
а
![]() – всіх можливих випадків,
– всіх можливих випадків,
![]() – число сприятливих випадків, що
конденсатори будуть по
.
– число сприятливих випадків, що
конденсатори будуть по
.
Тоді:
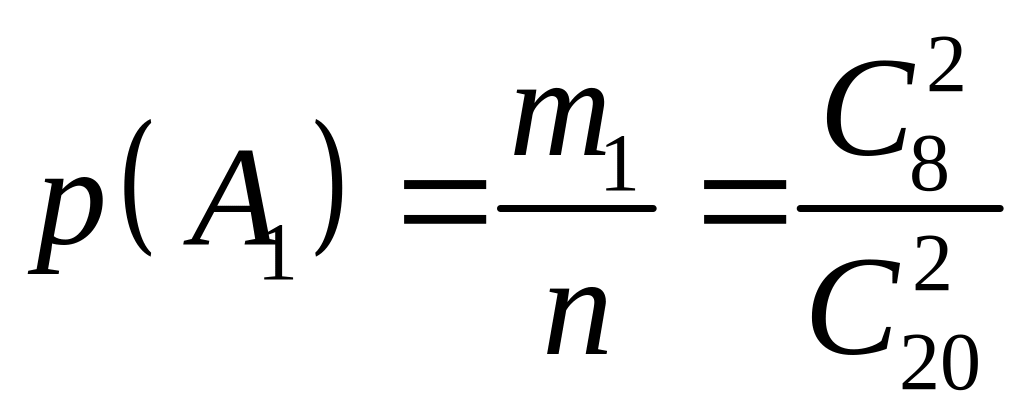 ,
,
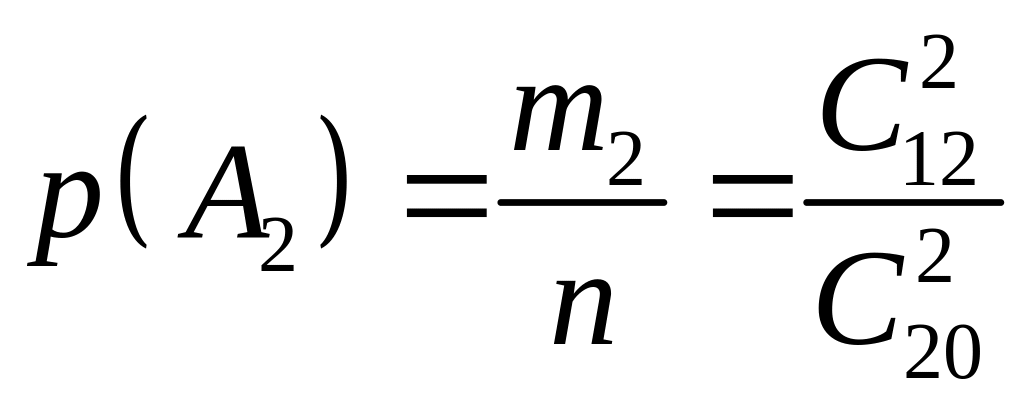 ,
,
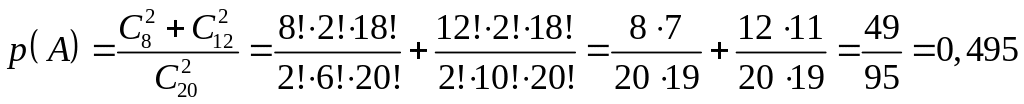 .
.
Зауваження. На практиці при обчисленні
ймовірностей деякої події
інколи доцільно спочатку обчислити
![]() ,
а потім обчислити
,
а потім обчислити
![]() .
.
Приклад 7. В коробці лежать
діодів, з них тільки
![]() придатних. Обчислити ймовірність того,
що з трьох взятих навмання діодів хоча
б один був придатний.
придатних. Обчислити ймовірність того,
що з трьох взятих навмання діодів хоча
б один був придатний.
Розв’язання. Нехай
– подія, яка полягає в тому, що серед
трьох діодів хоча б один був придатний.
Тоді
– подія, яка полягає в тому, що всі три
діоди браковані. Події
і
протилежні і
,
легко обчислити за класичною формулою.
Загальне число способів вилучення трьох
діодів із
,
![]() .
Оскільки бракованих діодів
.
Оскільки бракованих діодів
![]() шт., то число способів вилучення по три
бракованих діода
шт., то число способів вилучення по три
бракованих діода
![]() ,
тоді
,
тоді
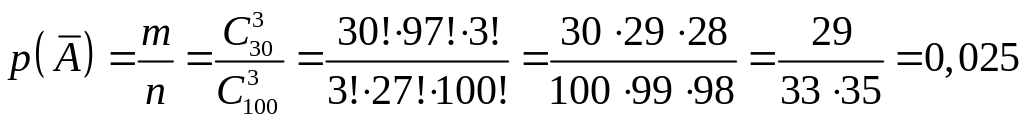 ,
а
,
а
![]() .
.
Приклад 8. В коробці лежать резистори
![]() шт., по
ком і
шт., по
ком і
![]() шт. по
ком. Навмання беруть
резистори. Обчислити ймовірність того,
що хоча б один з них був
ком.
шт. по
ком. Навмання беруть
резистори. Обчислити ймовірність того,
що хоча б один з них був
ком.
Розв’язання. Нехай – подія, яка полягає в тому, що з чотирьох взятих резисторів хоча б один був ком. Тоді – подія, яка полягає в тому, що всі чотири резистори по ком. Події і протилежні і . можна обчислити за класичною формулою.
![]() ,
,
![]() ,
тоді
,
тоді
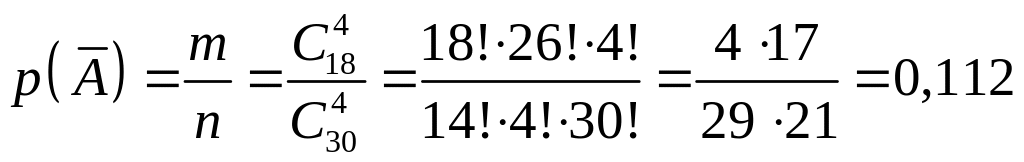 ,
,
![]() .
.
