
Доведення. У цьому випадку , тобто не один з наслідків випробування не сприяє події, тобто
![]() .
.
Для визначення значного і сприятливого числа випадків часто користуються формулами з теорії сполук.
3*. Основні поняття комбінаторики
Комбінаторика вивчає кількість сполучень відпорядкованих визначеним умовам, котрі можна скласти з елементів будь-якої природи, заданої кінцевої множини. При безпосередньому обчисленні ймовірностей часто використовують формули комбінаторики.
Розглянемо без доведення формули з теорії сполук. Сполуки елементів або випадків бувають трьох видів: переставлення, розміщення, комбінації.
Означення 9. Переставленням називають такі множини, що містять одні й ті ж різних елементів і які відрізняються лише порядком їх розташування.
Число усіх можливих перестановок
![]() .
.
Приклад. Утворити перестановки з
3-х елементів
![]() ,
,
![]() ,
,
![]() .
.
Розв’язання.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() – їх
.
– їх
.
![]() .
.
Означення 10. Комбінаціями з елементів по називають такі множини, кожна з яких містить елементів, і які відрізняються одна від одної принаймні одним елементом.
Число комбінацій з елементів по
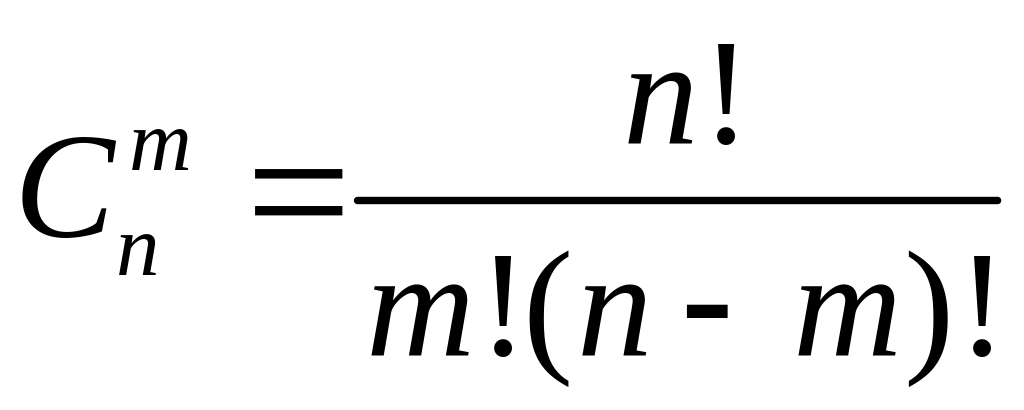 .
.
Приклад.
В групі
![]() студентів:
студентів:
![]() юнаків і
дівчат. Для поїздки на екскурсію
відбирають
чоловік. Знайти ймовірність того, що з
числа відібраних буде
юнаки і
дівчини.
юнаків і
дівчат. Для поїздки на екскурсію
відбирають
чоловік. Знайти ймовірність того, що з
числа відібраних буде
юнаки і
дівчини.
Розв’язання. .
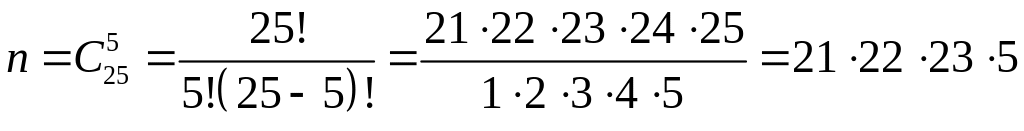 ;
;
![]() .
.
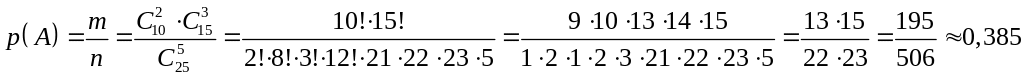 .
.
Означення 11. Розміщенням з елементів по елементів називають такі впорядковані множини, кожна з яких містить елементів, що відрізняються одна від другої або елементами або їх порядком
Число розміщень обчислюється за формулою
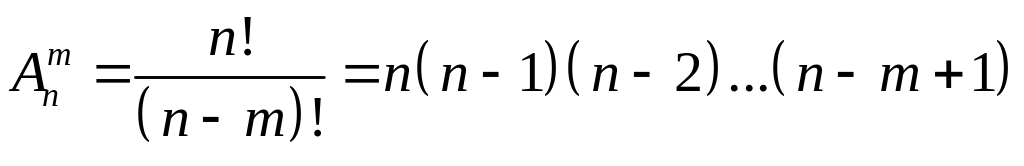 .
.
Приклад. Розглянемо елементи , , . Утворимо розміщення з трьох елементів по .
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() – їх шість
– їх шість
![]() .
.
Дамо ще одне означення перестановок.
Означення 12. Розміщення з елементів по називаються перестановками
![]()
Число розміщень, перестановок і комбінацій зв’язані рівністю
![]() .
.
Чим вирізняється означення класичної ймовірності від статичної?
Порівнюючи означення ймовірності і відносної частоти робимо висновок: означення ймовірності не потребує, щоб події відбувалися в дійсності. Означення ж відносної частоти припускає, що події відбулися фактично, тобто ймовірність обчислюється до події, а відносна частота – після події.
Властивість відносної частоти в тім, що в різних випробуваннях відносна частота змінюється мало (тим менше, чим більше проведено випробувань), коливається біля деякого сталого числа. Це стале число й є ймовірністю події.
