Моделювання форм статистичних розподілів
Статистичні розподіли можуть мати різні форми.
Найчастіше зустрічаються наступні форми розподілів:
монотонно спадна функція (намалювати графік);
монотонно зростаюча функція;
U-подібний розподіл;
J-подібний розподіл;
дзвоноподібний унімодальний;
двовершинний бімодальний;
багатовершинні розподіли.
Також розподіли можна розділити на дві основні групи:
симетричні;
асиметричні.
Для аналізу особливостей варіації значень та їхніх частот в межах того чи іншого статистичного розподілу достатньо часто маніпулюють тими чи іншими формами розподілу. При чім це виконують в два етапи:
1. Моделюють теоретичний (ймовірний, модельний) розподіл у відповідності до тих чи інших критеріїв. Найбільш відомими моделями є:
нормальний розподіл;
розподіл 2;
t-розподіл Ст’юдента;
F-розподіл Фішера.
2. Варіацію значень та їхніх частот в межах реального статистичного розподілу порівнюють до модельного (теоретичного). На підставі ступеня та характеру відмінності реального від модельного формулюють висновки про особливості варіації значень та їхніх частот в межах реального статистичного розподілу.
Нормальний розподіл – це такий статистичний розподіл, при якому більша частина значень групується довкола певного середнього, по обидві сторони від якого частота значень рівномірно та симетрично знижується.
99,73%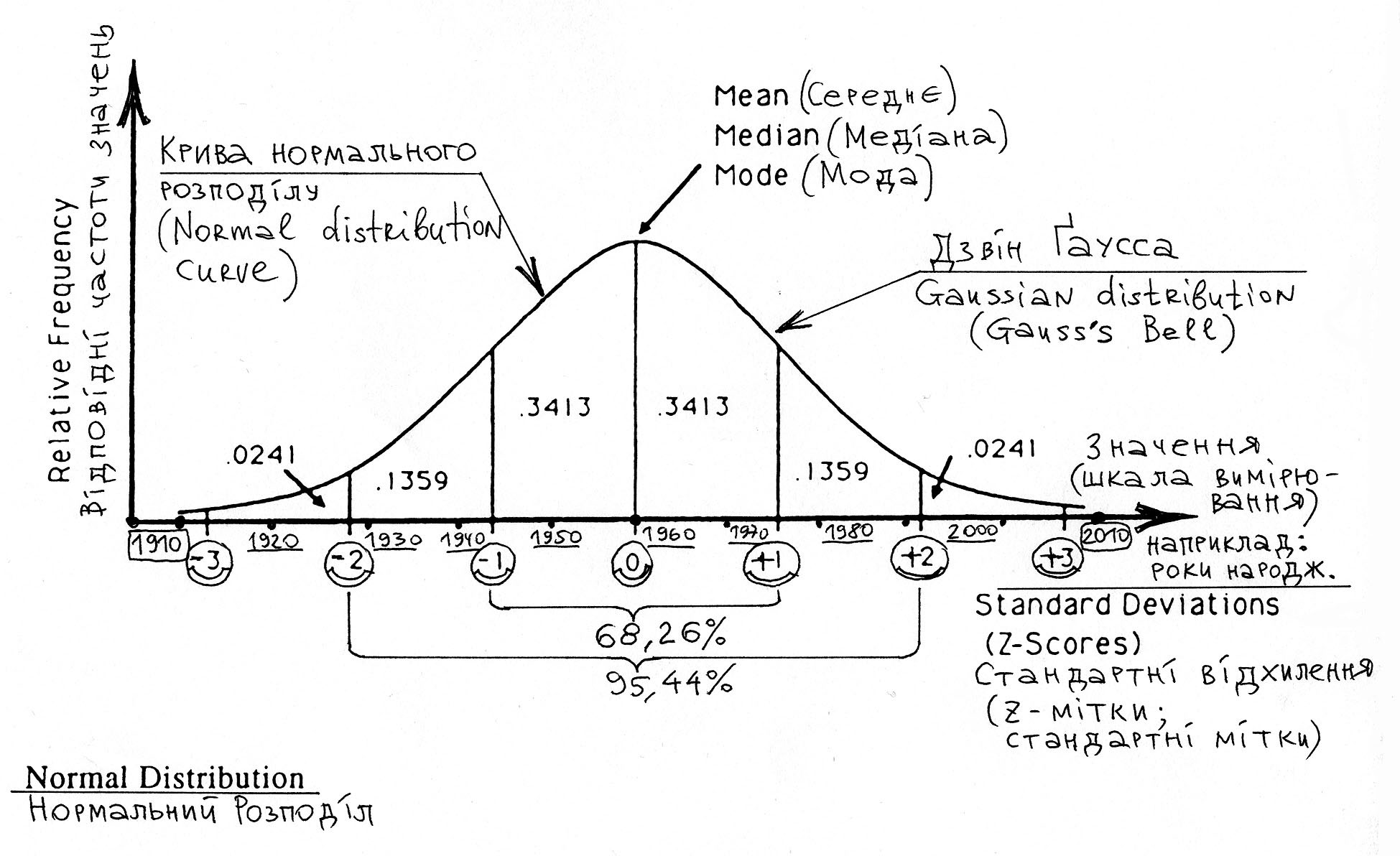
Повернення до Прикладу 10
Шкала: 10-11-12-13-14-15-16-17-18
Роз’яснення принципів побудови стандартного відхилення на зазначеній шкалі.
Роз’яснення важливості застосування міри “стандартне відхилення” одночасно з мірою “середнє” при проведенні порівняльного аналізу.
Міри розподілу
Skewness (Асиметрія/ зсув/ ухил)
Це є міра відхилення варіації значень та їхніх частот від симетричного розподілу. Якщо варіація значень та їхніх частот підкоряється нормальному розподілові, тоді асиметрія дорівнює нулю. Якщо вершина асиметричного розподілу є зсунутою в сторону менших значень, тоді можна говорити про позитивну (ліву) асиметрію; якщо в сторону більших – про негативну (праву).
Формула розрахунку асиметрії для ранжованого РР.
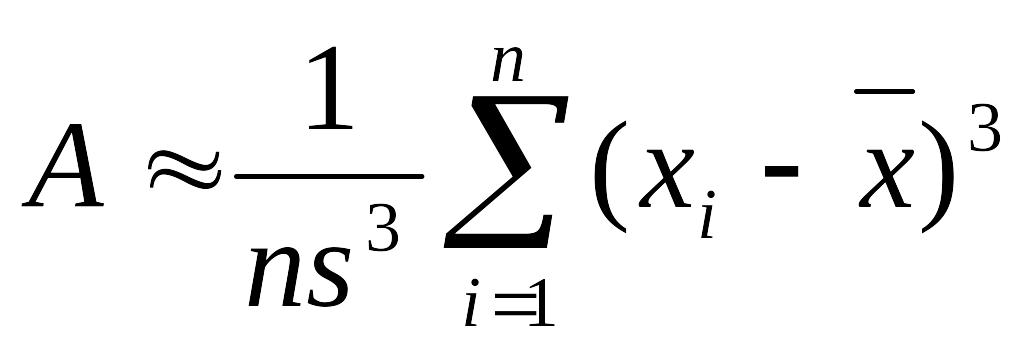
Приклад 11. Ранжований ряд років народжень: 1924, 1935, 1945, 1957, 1961, 1969, 1970, 1977, 1988, 1991.
Формула розрахунку асиметрії для варіаційного РР.
Приклад 12. За результатами спостереження за 35 підлітками... отримали наступний варіаційний ряд розподілу.
X |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
f |
1 |
2 |
5 |
7 |
9 |
6 |
3 |
0 |
2 |
Kurtosis (Ексцес/ крутизна)
Ексцес вказує на те, чи розподіл значень є пологим, чи крутим. Він дорівнює нулю, якщо є нормальний розподіл значень. Якщо розподіл значень є крутішим за нормальний розподіл, тоді ексцес є додатнім. Якщо розподіл значень є пологішим за нормальний розподіл, тоді ексцес є від’ємним.
Формула розрахунку ексцеса для ранжованого РР.
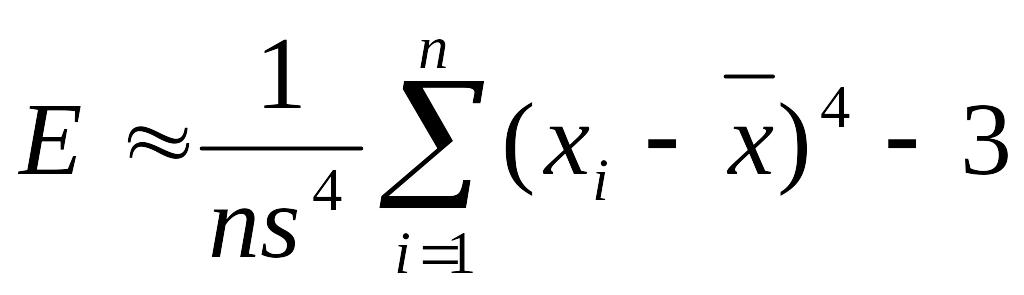
Для Прикладу 11.
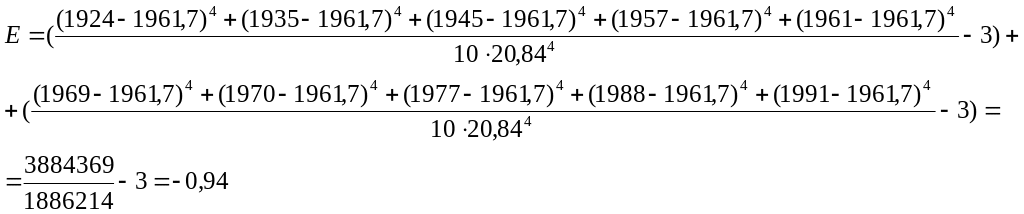
Формула розрахунку ексцеса для варіаційного РР.
Для Прикладу 12.
ЛОГІЧНИЙ ЗВ’ЯЗОК МІЖ МІРАМИ ОПИСОВОЇ СТАТИСТИКИ
Логічно між собою є пов’язаними:
середнє арифметичне та асиметрія;
дисперсія, стандартне відхилення, квартилі.