11

Тема 4. Описова статистика числових вибірок

При аналізі статистичних рядів розподілу (далі – статистичних розподілів) найуживанішими є наступні групи статистичних показників:

• частотні та відсоткові розподіли;

• міри центральної тенденції (середні величини);

• міри варіації (розсіювання);

• міри розподілу.

Частотні та відсоткові розподіли

Приклад 1. Ми вивчаємо рівень задоволеності львів’ян діяльністю мера їхнього міста. Для відповіді на наше запитання “Якою мірою Ви задоволені діяльністю мера міста Львова?” ми запропонували наступні варіанти відповіді:

1. Цілком задоволений/на

2. Скоріше задоволений/на, ніж не задоволений/на

3. Важко відповісти, задоволений/на чи ні

4. Скоріше не задоволений/на, ніж задоволений

5. Зовсім не задоволений/на

Відповіді респондентів на запитання ми впорядкували у форматі варіаційного ряду розподілу зі значеннями варіант та їхніми частотними й відсотковими розподілами:

Значення варіант	Розподіл частот (n)	Розподіл відсотків (%)
1	50	12,5
2	80	20,0
3	120	30,0
4	110	27,5
5	40	10,0
Сума (N)	400	100,0

Міри центральної тенденції (середні величини)

Середнє арифметичне.

Медіана.

Мода.

Середнє арифметичне

для ранжованого РР

M = ,

де х₁, х₂,... х_n – значення елементів статистичного розподілу,

n – загальна кількість елементів статистичного розподілу.

Приклад 2. Ранжований ряд років народжень: 1924, 1935, 1945, 1957, 1961, 1969, 1970, 1977, 1988, 1991.

для варіаційного РР

M = ,

де 1, 2, ... n – значення варіант (наприклад, елементи шкали вимірювання від 1 до 5),

f₁, f₂,... f_n – частота, з якою зустрічається відповідна варіанта,

N – загальна кількість випадків (одиниць спостереження).

Результатом є середнє на впорядкованому ряді значень варіант (на шкалі вимірювання).

Приклад 3.

Значення варіант	Розподіл частот (n)
1	50
2	80
3	120
4	110
5	40
Сума (N)	400

Середнє арифметичне обчислюється тільки для порядкових, інтервальних та метричних шкал.

Медіана

Median (Медіана) – Me

Медіана – це точка на статистичному розподілі, елементи якого упорядковано за мірою зростання їхніх значень, нижче та вище від якої розташовується по половині всіх виміряних значень. Якщо кількість елементів є непарною, тоді медіана завжди співпадає з одним із виміряних значень. При парній кількості елементів медіана буде середнім арифметичним двох сусідніх значень, що розташовуються в середині статистичного розподілу.

Приклад 4: 1-2-3-4-5-6-7.

Приклад 5: 1-2-3-4-(4,5)-5-6-7-8.

Приклад 6: стат. сукупність: 3, 9, 4, 9, 4, 8, 5, 8, 6, 7.

Впорядковуємо її за порядком зростання: 3-4-4-5-6-(6,5)-7-8-8-9-9.

Медіана в цьому випадку дорівнює: (6+7):2=6,5.

Таким чином, у однієї половини об’єктів статистичного розподілу – що розташовані ліворуч від медіани – значення є меншими за неї, а у іншої – що розташовані праворуч – більшими за медіану.

Медіана обчислюється тільки для порядкових, інтервальних та метричних шкал.

Мода

Mode (Мода) – Mo

Мода – це значення, яке найчастіше зустрічається у статистичному розподілу. Якщо однакова найбільша частота зустрічається у декількох значень, тоді обирається найменше з них.

Приклад 7: ряд – 3-4-4-5-6-7-8-8-9-9. Мода = 4.

Мода також може обчислюватись й для номінальних шкал.

Міри варіації (розсіювання)

Мінімум, максимум.

Варіаційний розмах.

Дисперсія.

Середнє квадратичне (стандартне) відхилення.

Коефіцієнт варіації.

Процентилі.

Квартилі.

Мінімум, максимум, варіаційний розмах

Мінімум (min) – найменше значення ознаки.

Максимум (max) – найбільше значення ознаки.

Варіаційний розмах (range) = max – min.

Приклад 8. Ранжований ряд років народжень: 1924, 1935, 1945, 1957, 1961, 1969, 1970, 1977, 1988, 1991.

Min = 1924; Max = 1991; Range = 1991–1924 = 67.

Дисперсія

(показник ступеня варіативності значень

статистичного розподілу)

Для ранжованого ряду

,

де ∑ – знак суми, х – значення елементів статистичного розподілу, М – середнє значення статистичного розподілу, N – загальна кількість елементів статистичного розподілу.

Приклад 9. Ранжований ряд років народжень: 1924, 1935, 1945, 1957, 1961, 1969, 1970, 1977, 1988, 1991.

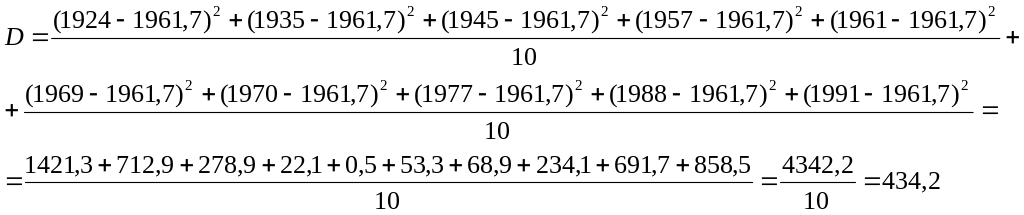
Для варіаційного ряду

,

де n – значення варіанти, М – середнє значення всіх елементів статистичного розподілу,

f_n – частота, з якою зустрічається відповідна варіанта, N – загальна кількість випадків (одиниць спостереження).

Приклад 10. За результатами спостереження за 35 підлітками (а згодом – молодими людьми) у віці від 10 до 18 років із щорічною фіксацією, на скільки кожний з них виріс, та визначенням віку, протягом якого у того чи іншого об’єкта спостереження відбулося максимальне збільшення зросту, отримали наступний варіаційний ряд розподілу.

X	10	11	12	13	14	15	16	17	18
f	1	2	5	7	9	6	3	0	2

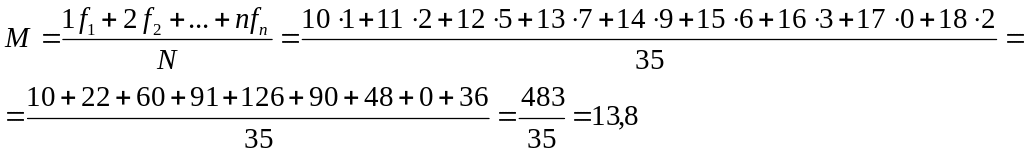
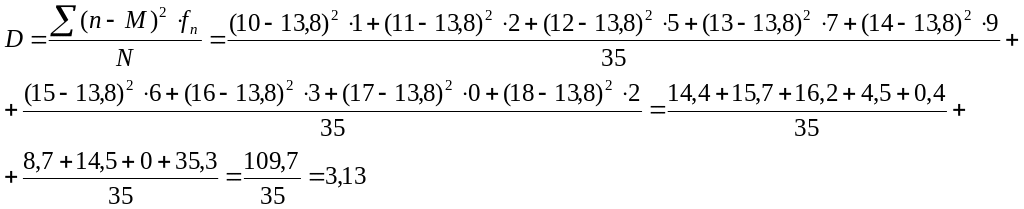
Чим більшим є значення дисперсії, тим активнішою є варіативність значень статистичного розподілу.

Розмірність дисперсії – квадрат розмірності значень статистичного розподілу.