32/ Первая космическая скорость

(круговая скорость) — скорость, которую необходимо придать объекту, который после этого не будет использовать реактивное движение, чтобы вывести его на круговую орбиту (пренебрегая сопротивлением атмосферы и вращением планеты). Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.

[Править]Вычисление

В инерциальной системе отсчёта на объект, движущийся по круговой орбите вокруг Земли будет действовать только одна сила — сила тяготения Земли. При этом движение объекта не будет ни равномерным, ни равноускоренным. Происходит это потому, что скорость и ускорение (величины не скалярные, а векторные) в данном случае не удовлетворяют условиям равномерности/равноускоренности движения — то есть движения с постоянной (по величине и направлению) скоростью/ускорением. Действительно — вектор скорости будет постоянно направлен по касательной к поверхности Земли, а вектор ускорения — перпендикулярно ему к центру Земли, при этом по мере движения по орбите эти вектора постоянно будут менять свое направление. Поэтому в инерциальной системе отсчета такое движение часто называют «движение по круговой орбите с постоянной по модулю скоростью»

Часто для удобства вычисления первой космической скорости переходят к рассмотрению этого движения в неинерциальной системе отсчета — относительно Земли. В этом случае объект на орбите будет находиться в состоянии покоя, так как на него будут действовать уже две силы: центробежная сила и сила тяготения. Соответственно, для вычисления первой космической скорости необходимо рассмотреть равенство этих сил.

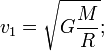
где m — масса объекта, M — масса планеты, G — гравитационная постоянная (6,67259·10⁻¹¹ м³·кг⁻¹·с⁻²),  — первая космическая скорость, R — радиус планеты. Подставляя численные значения (для Земли M = 5,97·10²⁴ кг, R = 6 371 км), найдем

 7,9 км/с

Первую космическую скорость можно определить через ускорение свободного падения — так как g = GM/R², то

.

Космические скорости могут быть вычислены и для поверхности других космических тел. Например на Луне v₁ = 1,680 км/с, v₂ = 2,375 км/с

Вторая космическая скорость (параболическая скорость, скорость освобождения, скорость убегания) — наименьшаяскорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела. Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).

Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для Солнца вторая космическая скорость составляет 617,7 км/с.

Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся попараболе относительно планеты.