5.3. Аппроксимация при помощи кривых и поверхностей Безье

Многочлены Безье используются для приближённой параметрической аппроксимации в том случае, когда нужно провести плавную кривую, проходящую вблизи множества точек – ориентиров. Французский математик Безье разработал их, выполняя исследования для фирмы «Рено».

В многочленах Безье в качестве базисных функций используются полиномы Бернштейна

B(m,p,i)=Cⁱ _m  (1-p)ⁱ  p^m-i , (5.13)

где Сⁱ_m = m! / [i! (m-i)!] - число сочетаний из i по m .

Полиномы Бернштейна могут быть интерпретирова-ны как слагаемые в биноме Ньютона следующего вида:

1^m = [(1-p)+ p] ^m = (1-p) ^m+ m(1-p)^m-1p+ 0,5m(m-1)(1-p)^m-2p² + . . . + m (1-p) p ^m-1+ p ^m

110

Допустим, заданы m+1 упорядоченная точка – ори-ентирP₀, P₁,…,P_m на плоскости 0xy. Координаты каждой точкиP_i=(x_i , y_i). Ломаная, которая последовательно соеди-няет точкиP₀, …,P_m (Рис.5.7), называется опорной:

Рис.5.7

Многочлен Безье вводится следующим образом:

Его можно представить как приведенный выше бином Ньютона, у которого каждое i-ое слагаемое умножается на

точкуP_i. Полиномы Бернштейна являются базисными функциями. Параметр кривой р изменяется на кривой в пределах 0  р  1. Уравнение справедливо для точек любой размерности – и для плоских и для пространственных. На Рис. 5.8 даны примеры кривых Безье для случаев m=3,4.

Свойства кривых Безье .

1. К ривая Безье проходит через первую и последнюю точку кривой: P(0)=P₀ , P(1)=P_m. Во внутренних точках кривой 0 < p <1.

111

Рис.5.8

2. В точках P(0)=P₀ , P(1)=P_m кривая касается, соответ-ственно, отрезков P₀P₁ , P_m-1P_m опорной ломаной.

3. Точность приближения многочлена Безье к точкам – ориентирам можно сколь угодно увеличить, вводя крат-ные точки, когда в одной физической точке распола-гается не одна , а несколько точек - ориентиров.

4. Сумма коэффициентов в кривых Безье всегда равна 1. Это следует из вышеприведенного бинома Ньютона.

Н а Рис.5.9 показано изменение формы многочлена Безье при кратности средней точки , равной 1,2,3 (кривые 1,

Рис.5.9

112

2,3). Если в каждой точке-ориентире кратность устремить к бесконечности, то многочлен Безье в пределе будет стре-миться к опорной ломаной.

C физической точки зрения многочлен Безье можно представить в виде ленты из магнитного материала, а точки- ориентиры – в виде одинаковых магнитов , притягивающих ленту. Чем выше кратность точки, тем сильнее она притя-гивает ленту.

Поверхности Безье, как и кривые, используются в тех случаях, где требуется не точное прохождение поверхности через множество заданных пространственных точек, а полу-чение гладких поверхностей эстетичного вида, проходящих вблизи этих точек. Они определяются как тензорное произ-ведение двух полиномов Безье с использованием двух пара-метров u и v :

г де {Р_{i j} } - двумерный список точек в пространстве, с по-мощью которого задаётся поверхность, а (m+1) и (n+1) – количество точек по u и v.

Поверхность Безье, как и кривая, точно проходит только через крайние (угловые) точки заданной матрицы. Например, для m=n=2 (Рис.5.10) уравнение поверхности следующее:

где - матрица из координат опорных

113

точек.

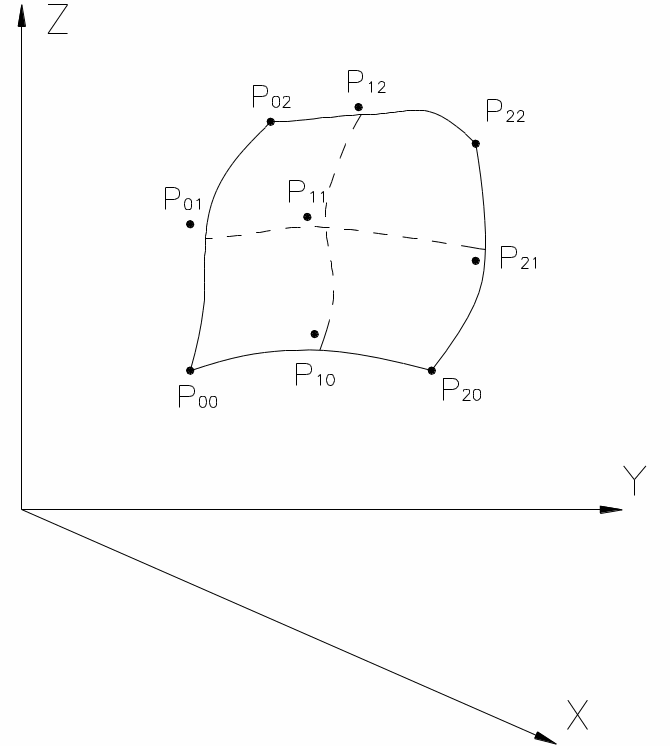
Рис 5.10

Для визуализации поверхности на ней проводятся линии уровня. Линии уровня по u описываются уравнением:

где v₀=const, 0 ≤ u ≤ 1.

Линии уровня по v вводятся аналогично:

114

u₀ = const, 0 ≤ v ≤ 1.

Программы на языке AutoLISP для построения плос-кой и пространственной кривой Безье в среде AutoCAD да-ны в Приложении (bez_2d, bez_3d) . Функция BEZP на языке Autolisp для построения линий уровня поверхности Безье, проекций её линий уровня на плоскость z=0 и соот-ветствующая отладочная функция также приведены в Приложении.

Задачи.

1. В чем принципиальное отличие аппроксимации при помощи кривых и поверхностей Безье от равномерного и среднеквадратичного приближений ?

2. Строго доказать, что любая кривая Безье проходит через первую и последнюю точку опорной ломаной: P(0)=P₀ , P(1) = P_m.

3. В общем случае при отсутствии кратных точек на опор-ной ломаной кривая Безье не проходит точно через её про-межуточные точки. Построить пример, в котором кривая Безье точно проходит через промежуточную точку опорной ломаной – например при p = 0,5. Дать строгое обоснование примера.

4. Доказать на примере случая m = n = 2, что поверхность Безье точно проходит через крайние (угловые) точки заданной двухмерной матрицы точек {Р_ij }.

5. Написать программу, рекурсивно вычисляющую для за-данного m последовательность чисел сочетаний С⁰_m , С¹_m , С² _m ,…, С^m-1 _m , С^m _{m .}

6. C помощью программы bez_2d смоделировать плоские кривые, близкие по форме к: а) цифре “8”, б) цифе “3”, в) цифре “6”, г) букве “с”, д) букве “е”, д) букве “s”.

115