7.3. Построение проективных векторных изображений трёхмерных объектов

Как отмечено в п.6.4, с точки зрения упрощения ли-нейных преобразований объектов, их геометрию необхо-димо задавать в виде:

1) набора однородных координат точек

P = {P₀ ,P₁ ,…,P_n},

гдеP_i = (x_i , y_i , z_i ,1),

(n+1) - общее число точек и

2) списка пар номеров точек, которые соединяются между собой отрезками,

L={I₀,I_1,…,I_m},

где I_j=(i_j0,i_j1); i_j0, i_j1 - номера конечных точек линии j в наборе P_i ;

(m+1) – общее число линий.

При выполнении совокупности линейных и проек-тивных преобразований необходимо:

I. Определить результирующую матрицу преобразований. Допустим, наборы (списки) P и L, описывающие геомет-рию объекта заданы. Если необходимо выполнить несколь-ко линейных и проективных преобразований T₁,…,T_k объек-та, то необходимо

а) вначале найти матрицы элементарных преобразований

M_T1 , M_T2 ,… , M_Tk ;

б) затем - результирующую матрицу преобразования в виде их произведения

M_T = M_Tk … M_T2 M_T1 .

148

Замечание. Порядок матриц в произведении – обратный по-рядку выполнения преобразований. Это обусловлено при-нятой последовательностью умножения матриц на вектор – слева.

II. В цикле по j от 0 до n умножить векторы однородных координат точек P_i (i=0,1,…, n) на матрицу М_Т и занести преобразованные координаты точек в новый массив

P_n={P_n0 ,P_n1, … ,P_nn } .

III. Если необходимо (в случае нелинейных проективных преобразований) – нормировать координаты точек P_ni по четвёртой компоненте.

IV. Выделить из координат P_ni двумерные компоненты, необходимые для построения проекции.

V. По списку L и списку двумерных координат точек по-строить искомое векторное изображение проекции объекта.

Пример. Задан куб (Рис. 7.1) с вершинами в точках А(0,0,0), В(0,100,0), С(100,100,0), D(100,0,0), E(0,0,100), F(0,100,100), G(100,100,100), H(100,0,100).

Требуется последовательно выполнить следующие элемен-тарные преобразования каркасной модели объекта:

1) поворот вокруг оси Х на угол 30⁰;

2) поворот вокруг оси Y на угол 60⁰;

3) поворот вокруг оси Z на угол 45⁰;

4) сдвиг на вектор (200, 100 , 50);

5) ортогональную проекцию на плоскость z = 0.

Решение.

Ниже дан текст соответствующей функции kub на языке Autolisp.

149

Алгоритм её работы следующий:

1. Строится список spp координат точек куба A, B, C, D, E, F, G, H.

2. Строится список пар номеров spl = ( l₀, l₁,…, l₁₁) пар вер-шин, образующих линии-рёбра куба.

3. С помощью стандартных функций rx, ry, rz, s, orz строятся матрицы элементарных преобразований mrx, mry, mrz, ms ,morz , осуществляющих преобразования 1) -5).

С помощью функции векторной алгебры умножения матриц mm определяется итоговая матрица преобразования mrez.

4. С помощью функции векторной алгебры умножения матрицы на вектор mv определяются новые координаты точек (список sppn).

6. По списку линий spl и списку sppn координат строятся:

a) двухмерные проективные координаты проекций вершин куба (x_i,y_i);

б) векторы – линии требуемой проекции модели.

Текст функции kub

(defun c:kub ()

;Формирование списка однородных коор-т точек куба (spp)

(setq a (list 0 0 0 1) b (list 100 0 0 1) c (list 100 100 0 1) d (list 0 100 0 1) e (list 0 0 100 1) f (list 100 0 100 1) g (list 100 100 100 1) h (list 100 0 100 1) spp (list a b c d e f g h ))

;Формирование списка пар точек в линиях (spl)

(setq l0 (list 0 1) l1 (list 1 2) l2 (list 2 3) l3 (list 3 0) l4 (list 4 5) l5 (list 5 6) l6 (list 6 7) l7 (list 7 4) l8 (list 0 4) l9 (list 1 5) l10 (list 2 6) l11 (list 3 7)spl (list l0 l1 l2 l3 l4 l5 l6 l7 l8 l9 l10 l11 ))

;Расчет матриц элементарных преобразований (mrx, mry, mrz, ms, morz)

(rx (/ pi 6)) (ry (/ pi 3)) (rx (/ pi 4)) (s 200. 100.50.) (orz 0)

150

;Расчет итоговой матрицы сложного преобразования (mrеz)

(mm mry mrx 4) (mm mrz mrez 4) (mm ms mrez 4) (mm morz mrez 4)

;Пересчет координат точек (из массива spp в массив sppn)

(setq i 8) (repeat 8 (progn

(setq i (- i 1)) pt (nth i spp)

(mv mrez pt 4) (setq sppn (cons vec sppn))

))

;Вычерчивание линий (пары номеров точек –из массива spl ,

; новые координаты – из массива sppn

setq i 12) (repeat 12 (progn

(setq i (- i 1)) nomp (nth i spl)

; В цикле - извлечение полных однородных координат ;(x,y,z,1) краевых точек линий и формирование их 2-мерных ;координат (x,y)

(setq p1 (nth (nth 0 nomp) sppn) p2 (nth (nth 1 nomp) sppn))

(setq pt1 (list (nth 0 p1) (nth 1 p1)) pt2 (list (nth 0 p2) (nth 1 p2))

; В цикле - вычерчивание линий

(command «line» pt1 pt2 «»)

)) )

В результате выполнения данной функции получаем тре-буемое графическое изображение куба (Рис. 7.5).

Задачи.

I. По заданному типу геометрического объекта и набору его вершин:

а) построить каркасную модель (при помощи списков однородных координат вершин и пар номеров вершин, отражающих все рёбра);

б) построить матрицы всех элементарных преобразований и итоговую мастрицу сложного преобразования;

в) найти проективные координаты вершин объекта и построить его заданную проекцию.

151

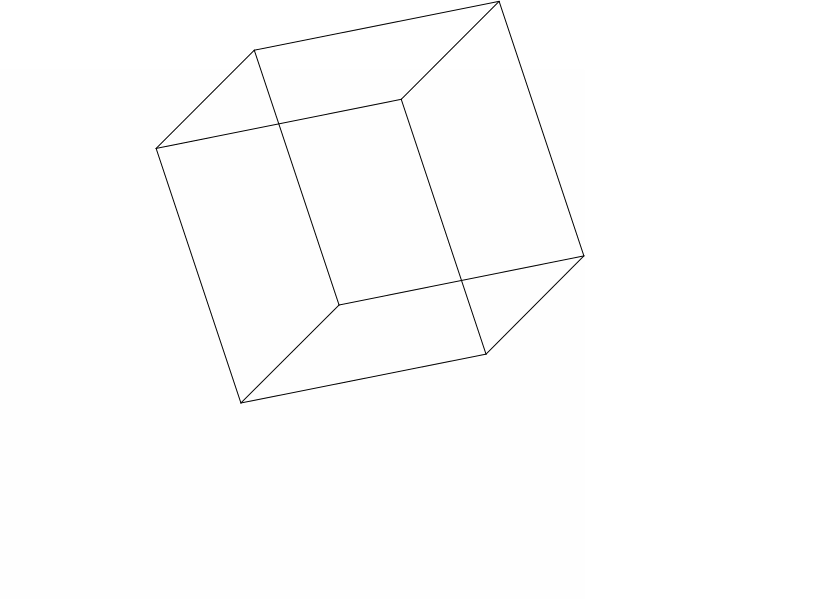
Рис.7.5

1. Задана пирамида с вершинами А(300,100,0), B(200,100,0), C(200,200,0), D(300,200,0), Е(250,150,200).

Требуется: а) повернуть её вокруг ребра AD на угол 60⁰; б) сдвинуть на вектор (-200,100,200); в) построить изомет-рическую проекцию.

2. Задана пирамида с вершинами А(100,100,100), B(200, 130, 100), C(120,200,100), D(100,100,200).

Требуется: а) повернуть её вокруг ребра AD на угол 150⁰; б) построить угловую пространственную проекцию с точками схода (500,0,0), (0,0,500).

3. Задана пирамида с вершинами А(50,50,0), B(50, 100, 0), C(100, 100, 0), D(100,50,0), E(75,75,100) .

Требуется: а) сдвинуть её на вектор (200,500,300); б) по-строить диметрическую проекцию с величиной коэффици-ента k = 1/4.

152

4. Задана пирамида с вершинами А(60,60,100), B(60, 120,120), C(100,90,140), D(80,80,200).

Требуется: а) повернуть её вокруг оси, проходящей через точки Е=(0,0,0) и F=(0,100,0), на угол 120⁰; б) построить изометрическую проекцию.

5. Задана пирамида с вершинами А(100,100,100), B(200, 100, 100), C(100,200,100), D(100,100,200).

Требуется: а) повернуть её на угол 120⁰ вокруг ребра АD; б) сдвинуть на вектор (200,100,300); в) построить димет-рическую проекцию с величиной коэффициента k = 0,2.

6. Задана пирамида с вершинами А(100,200,100), B(200, 200, 100), C(200,100,100), D(200,200,400).

Требуется: повернуть её на угол 150⁰ вокруг ребра ВD и построить изометрическую проекцию.

7. Задана призма с вершинами А(20,30,0), B(120,30,0), C(70, 100, 0), D(20,30,100), Е(120,30,100), F(70,100,100).

Требуется:а) повернуть её вокруг ребра CF на угол 105⁰; б) построить угловую перспективу с точками схода (200,0,0) и (0,400,0).

8. Задана призма с вершинами А(50,50,0), B(50,150,0), C(150,50,0), D(50,50,100), Е(50,150,100), F(150,50,100) .

Требуется: а) повернуть её вокруг ребра AB на угол 45⁰; б) повернуть вокруг оси Х на угол 60⁰; в) сдвинуть на вектор (200,100,50); г) ортогонально спроектировать на плоскость Z=0.

9. Задана призма с вершинами А(100,0,0), B(0,100,0), C(100, 100,0), D(100,0,200), Е(0,100,200), F(100,100,200) .

Требуется: а) повернуть её вокруг ребра CF на угол 150⁰; б)

повернуть вокруг оси X на угол 30⁰; в) построить диметри-

153

ческую проекцию с коэффициентом k=1/3.

10. Задан параллелепипед с вершинами А(0,0,0), B(0,2,0), C(1, 2,0), D(1,0,0), Е(0,0,3), F(0,2,3), G(1,2,3), H(1,0,3) .

Требуется: а) масштабно увеличить его с коэффициентами (50, 60, 40); б) сдвинуть на вектор (100,50,200); в) построить ортогональную проекцию на плоскость Z=0; г) построить косую перспективу с точками схода (100,0,0), (0,200,0), (0,0,300).

11. Задан параллелепипед с вершинами А(10,10,0), B(110, 10, 0), C(110,60,0), D(10,60,0), Е(10,10,100), F(110,10,100), G(110, 60,100), H(10,60,100).

Требуется: а) повернуть его вокруг ребра DH на угол 160⁰; б) сдвинуть на вектор (50, 50, 50), в) изометрически спроек-тировать.

12. Задана призма с основанием в виде правильного шести-угольника ABCDEF с центром O в точке (200,200,100) и длиной стороны, равной 50. Стороны AB, DЕ параллельны оси х. Высота призмы равна 400.

Требуется: а) построить ортогональную проекцию на плос-кость 0ху, б) построить угловую перспективу с точками схо-да (500,0,0) и (0,600,0).

13. Задана призма с основанием в виде пятиугольника, образованного точками А(0,0,0), B(200,0,0), C(200, 100, 0), D(100,200,0), Е(0,200,0). Высота призмы равна 200.

Требуется: построить угловую перспективу с точками схо-да (600,0,0) и (0,800,0).

II. Объект задан вершинами А(50,50,0), B(250,150,0), C(150, 50, 0), D(100,100,100), Е(200,120,150) и рёбрами AB, BC, AC, AD, DC, DE, CE, BE, DB.

Требуется: а) повернуть его вокруг ребра AС на угол 60⁰; б) сдвинуть на вектор (100,400,100); в) построить изомет-рическую проекцию.

154