Куб Диметрическая проекция

Рис. 7.1

138

При создании функции, формирующей матрицы диметрических проективных преобразований, необходимо учесть, что в языке Autolisp отсутствует стандартная функ-ция arccos. Для перехода к имеющейся обратной тригоно-метрической функции arctg (в Autolisp - ATAN) с учётом того, что искомые углы лежат в интервале [0,90], необходимо применить тригонометрическое соотношение:

Текст функции dimetr дан в Приложении.

Задачи.

1.Найти значения углов φ и ξ для коэффициента k=1/3.

2.Может ли величина k быть равной нулю? Ответ пояснить.

7.1. 3. Изометрическая проекция

Центр проецирования в изометрической проекции находится на бесконечности, равноудаленной от всех трех осей, поэтому показатели искажения равны друг другу (U=V=W). Для определения коэффициентов искажения составим систему уравнений, добавив дополнительное условие: U² + V² + W² = 2.

U = V =W;

U² + V² + W² = 2.

Решением системы являются следующие значения:

(7.7)

Поскольку изометрическая проекция является част-ным случаем диметрической проекции при k =1, то её можно выполнить аналогично – поворотами вокруг осей x и y с последующим ортогональным проецированием на плоскость z = 0 . Подставляя в выражения (7.4.а) и (7.4.б) для углов поворота ξ и φ значение k =1, получим :

139

ξ =arccosU=arccos φ=0,5*arccos(0)=/4. (7.8)

7.2. Перспективные проекции

Аксонометрические проекции хорошо передают фор-му объекта в том случае, когда расстояние от него до на-блюдателя значительно превосходит характерные размеры объекта. При таком удалении все его элементы искажаются примерно одинаково. Если же наблюдатель находится вблизи объекта, то это условие нарушается. Близкие и удалённые детали объекта искажаются с заметными разли-чиями. В этом случае для большей реалистичности необхо-димо использовать перспективные проекции. У них, в отличие от аксонометрических, центр проекции занимает положение с конечными координатами по всем осям. Перспективными изображениями часто пользуются худож-ники и архитекторы, так как эти изображения для близких объектов позволяют получить картину, близкую к реальной. В машинной графике данные проекции также используются для создания реалистических изображений.

Перспективное проецирование не является линейным преобразованием, поскольку коэффициенты искажения для отрезков, по разному удалённых от наблюдателя, будут раз-личными. Вследствие этого его невозможно выполнить пу-тем обычного однократного умножения однородных коор-динат точек на некоторую матрицу. На практике вначале исходные однородные координаты точек (x, y, z, 1) путем матричного умножения переводят в специальные промежу-точные координаты (x_п, y_п, z_п, Н), у которых четвёртая компонента не равна 1. Затем путем нормирования вектора промежуточных координат по четвертой компоненте полу-

140

чают требуемые перспективные однородные координаты точек (x^*, y^*, z^*,1).

Рассмотрим для примера положение центра проеци-рования O_p на оси z в точке с координатами (0,0,-k). До-пустим, плоскостью проецирования является плоскость z=0. Выясним для произвольной точки P = (x, y, z), какие коор-динаты будет иметь её изображение - точка P^* = (x*, y*, z*=0) - на плоскости проецирования (Рис.7.2). Рассматривая подобные треугольники О_POC , О_PAВ и учитывая, что OC =x* , AB = x , получим: О_PO : О_PA =OC : AB; k : (z+k) =x* : x . Отсюда следует: x^* = x/(z/k+1) . Рассматривая анало-гичные подобные треугольники О_PСР* , О_PВР с учётом ВР = у , СР* = у* , получим такое же выражение для проекции координат по оси у : у^* = у/(z/k+1).

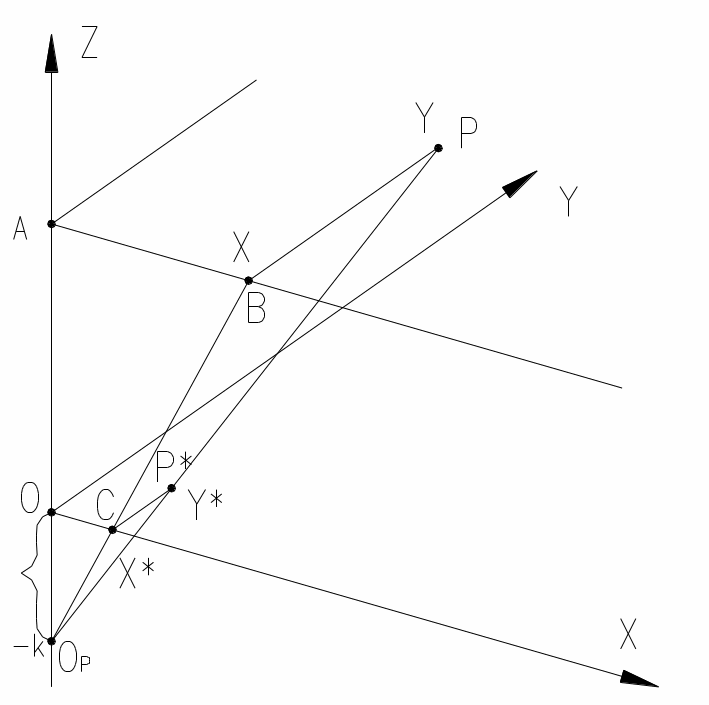
Рис.7.2

141

Введем для упрощения записи выражений величину r=1/k. Данное преобразование можно представить в виде последовательного выполнения двух.

1. Определение промежуточных координат точек в проек-тивной проекции на плоскость z=0 путём умножения исходных однородных координат на матрицу:

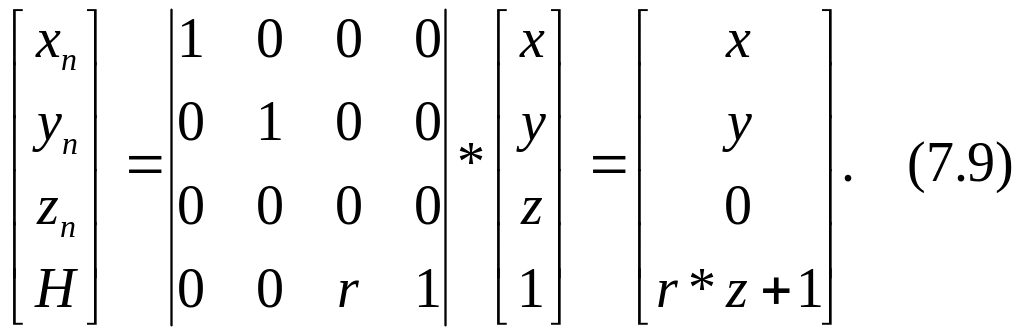
2. Деление всех промежуточных координат точек на ве-личину H – четвертую неединичную компоненту промежу-точных координат. В итоге получаются искомые перспек-тивные однородные координаты:

x^* =x_n /H =x/(r_* z+1), y^* =y_n /H = y/(r_* z+1), z^* =0. (7.10)

Из (7.10) видно, что в рассмотренном примере преоб-разование координат x, y зависит от того, какое положение точка занимает по оси z. Следовательно, в отличие от аксонометрических проекций, у перспективных преобразо-ваний изменения координат не являются одинаковыми для всех точек наблюдаемого объекта.

Плоская проекция не всегда удобна, так как линии, перпендикулярные плоскости z=0, вырождаются в точки. Для практики больший интерес представляет простран-ственное перспективное преобразование вида

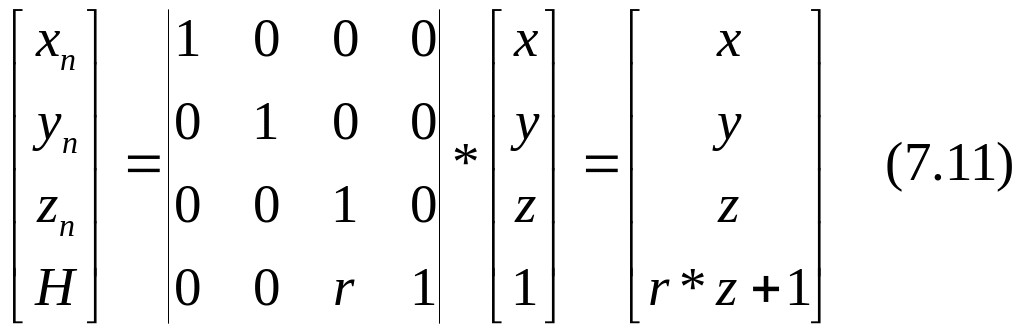
с однородными координатами

142

(x^*,y^*,z^*,1) = (x_n /(r_* z+1), y_n /(r_* z+1), z_n /(r_* z+1),1) (7.12).

Начало системы координат (0, 0, 0, 1) снова остается неизменным, а бесконечно удаленная по оси z точка (0, 0, 1, 0) преобразуется в точку [x_n , y_n , z_n , H] = [0, 0, 1, r] с однородными координатами (x^*, y^*, z^*, 1) = (0, 0, 1/r, 1) на оси z^*. Это означает, что положительная полуплоскость(0 ≤ z ≤ ∞) проецируется в ограниченную область(0 ≤ z^* ≤ 1/r). Кроме того, линии, которые первоначально были парал-лельны оси, теперь будут проходить через точку V_P = [0, 0, 1/r, 1]. Эту точку называют точкой схода перспективно-го преобразования. Плоскость z = 0 является проекцион-ной плоскостью, при этом центр проекции О_Р находится на той же самой оси, что и точка схода, на одинаковом рас-стоянии от противоположной стороны нулевой плоскости. Это иллюстрирует Рис.7.3. Рассмотрим произвольную точку А=(x,y,z). Координаты ортогональной (A**), плоской (A*) и пространственной (B*) перспективных проекций этой точки будут следующими:

A** =(x,y,0), A*=(x,y,0)/(r_* z+1), B*=(x,y,z)/(r_* z+1).

Длины отрезков ОА*, ОА** и А*А** можно выразить через координаты исходной точки А:

Из подобия треугольников ОА**V_P и А*А**В* следует справедливость пропорции ОА**/A*A** = OV_p/A*B*. Отсю-да получим: OV_p = A*B* ОА**/A*A** = OV_p = 1/r. Посто-янное положение точки сходаV_p следует из произвольнос-ти выбранной точки А.

143

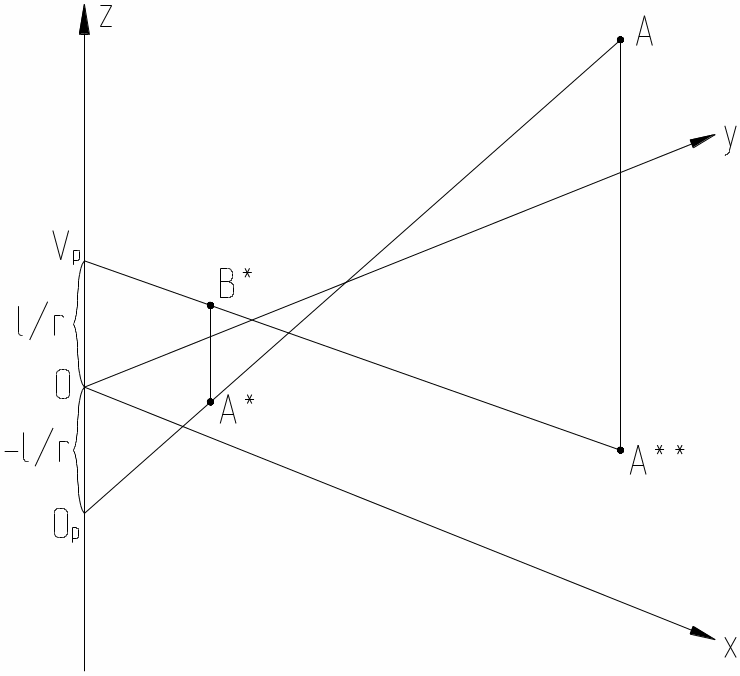
Рис.7.3.

Аналогично, перспективное преобразование

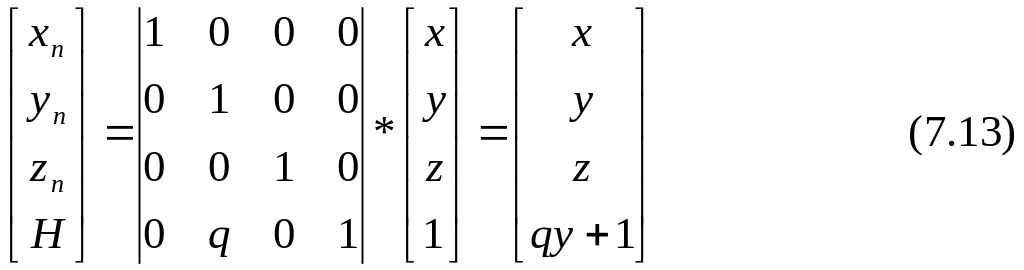
с однородными координатами

(x^*, y^*, z^*,1) = ( x_n /(q_* y+1), y_n /(q_* y+1), z_n /(q_* y+1), 1)

(7.14)

будет приводить к точке схода на оси y c координатами (0, 1/q, 0, 1).

144

Перспективное преобразование

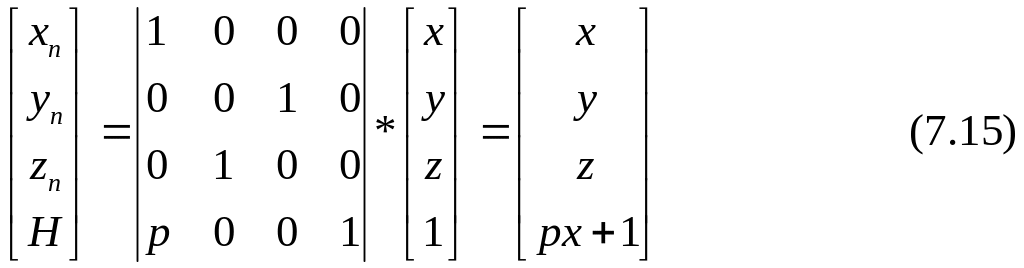
с однородными координатами

(x^*,y^*,z^*,1) = (x_n /(p_* x+1),y_n /(p_* x+1),z_n /(p_* x+1),1) (7.16)

приводит к точке схода на оси x с координатами (1/p, 0, 0, 1).

Преобразования, заданные уравнениями (7.11)-(7.16), называют одноточечными перспективными.

Если два элемента в четвертой строке преобразования матрицы являются ненулевыми, то получается двухточеч-ная или угловая перспектива.

Двухточечное перспективное преобразование

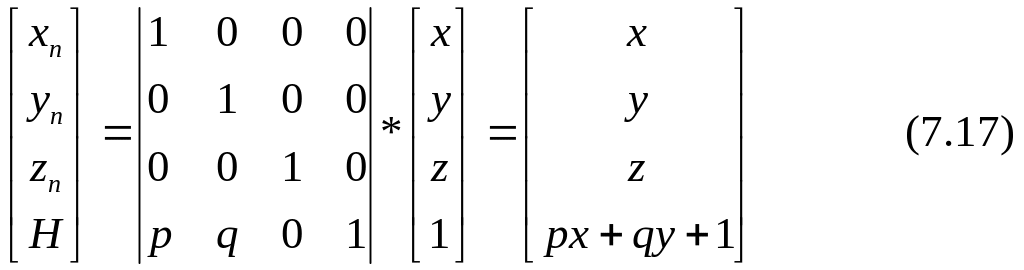
с однородными координатами

(x^*,y^*,z^*,1)=(x_n /(p_*x+q_*y+1),y_n/(p_*x+q_*y+1),z_n /(p_* x+q_* y+1),1)

(7.18)

приводит к двум точкам схода: одна расположена на оси x, в точке с координатами(1/p, 0, 0, 1), а другая – на оси y, в точке с координатами (0, 1/q, 0, 1).

Двухточеченые преобразования с точками схода по осям х, z и y, z строятся аналогично.

Если все три первых элемента 4-ой строки матрицы преобразования ненулевые, то получается трехточечная, или косая перспектива.

145

Трехточечное преобразование c матрицей

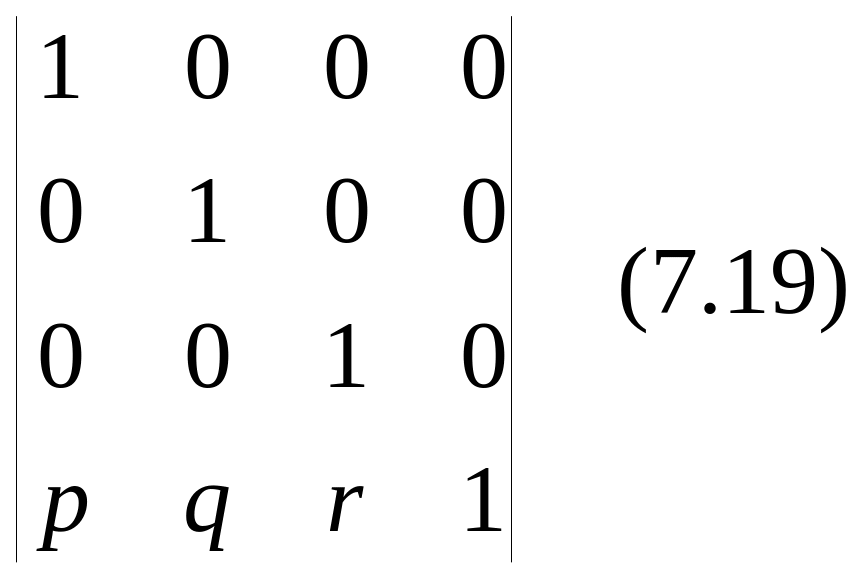
и однородными координатами

(x^*, y^*, z^*,1) = (x_n /(p_* x+q_* y+r_* z), y_n /(p_* x+q_* y+r_* z), z_n /(p_* x+q_* y+r_* z), 1) (7.20)

приводит к трем точкам схода: одна на оси x с координа-тами (1/p ,0, 0, 1), другая на оси y с координатами (0, 1/q, 0, 1) и третья на оси z в точке с координатами (0, 0, 1/r, 1). Трехточечное перспективное изображение единичного ку-ба, у которого начало совпадает с началом системы коор-динат, а оси ориентированы по осям координат, показано на Рис.7.4.

При практическом построении перспективных проек-ций первое матричное преобразование может быть опуще-но, поскольку оно фактически не изменяет координат точек, а только формирует нормирующий делитель. Поэтому для перехода к проекции достаточно для каждой точки сразу выполнить нормирование исходных координат. Все пер-спективные преобразования могут быть представлены как частные случаи трёхточечного при нулевых значениях со-ответствующих коэффициентов по осям.

Функция Persp на языке Autolisp, строящая трёхточеч-ное проективное изображение каркасной модели произволь-ного объекта (заданного соответствующими списками вер-шин и рёбер), приведена в Приложении. Для построения с её помощью одно- и двухточеченых перспективных проек-ций достаточно принять нулю её соответствующие пара-метры p, q, r .

146

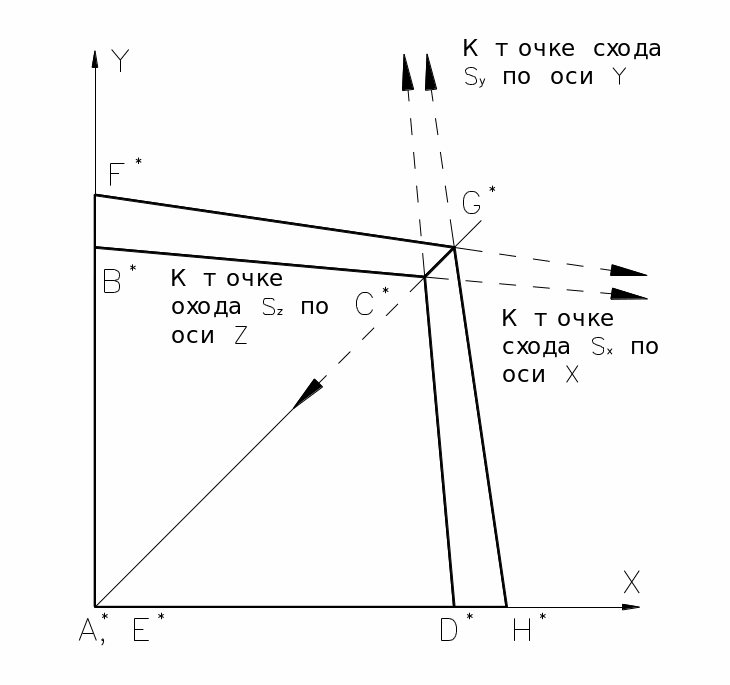Рис.7.4.

При визуализации объектов наряду с проецированием форма крупных объектов дополнительно характеризуется различной яркостью деталей, имеющих разную глубину (расстояние от наблюдателя) – близкие детали должны быть более яркими, удалённые – менее яркими. При этом на не-котором предельном удалении детали отсекаются – вообще не выводятся на экран. Также форма сложных объектов хо-рошо иллюстрируется при помощи задания объекту пере-мещений (вращательных, поступательных, сложных) отно-сительно наблюдателя. При этом лучше видны связи между деталями, различная скорость перемещения дополнительно характеризует их удалённость относительно наблюдателя.

147