15. Проекции с числовыми отметками. Построение точек пересечения прямой с поверхностью.

Сущность метода проекций с числовыми отметками заключается в том, что любая точка пространства проецируется ортогонально на одну горизонтальную плоскость, называемую плоскостью нулевого уровня. Положение точки по отношению к этой плоскости определяется числовой отметкой, проставляемой у буквенного обозначения проекции точки и представляющую собой число единиц расстояния от точки до плоскости проекций.

Построение точек пересечения прямой линии с топографической поверхностью в проекциях с числовыми отметками основано на использовании способа вспомогательных секущих плоскостей или же с помощью построения профиля поверхности.

Рассмотри оба этих способа. Задана прямая АВ и топографическая поверхность своими горизонталями. Определить точку встречи прямой и поверхности.

Первый способ (рисунок 7.46): через прямую АВ проведем вспомогательную секущую плоскость общего положения. Для этого проградуируем прямую АВ, проведем через данные точки градуировки горизонтали, параллельные между собой в любом направлении, но таким образом, чтобы одноименные горизонтали плоскости и поверхности пересеклись в пределах чертежа. Строим линию пересечения поверхности со вспомогательной плоскостью. Для этого отметим точки пересечения С и D – пересечения горизонтали плоскости и поверхности, имеющие одинаковые отметки. Полученная плавная кривая линия является линией пересечения поверхности плоскостью.

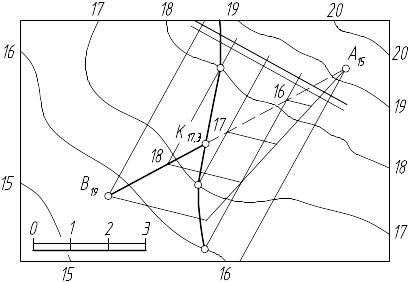
Рисунок 7.46

Точкой встречи прямой АВ с поверхностью будет точка К, полученная пересечением линии CD с прямой АВ ( по свойству инцидентности ).

Второй способ: через прямую АВ (рисунок 7.47 а,б) проводим проеци­рующую плоскость Q_i и строим профиль топографической поверхности (направлением профилирования будет прямая АВ). Через точки пересечения проекции следа плоскости Q_i с горизонталями поверхности на плане откладываем в масштабе чертежа по перпендикулярам к проекции прямой высотные отметки точек, равные отметкам горизонталей. Соединив полученные точки плавной кривой, получим профиль поверхности. Таким же образом строим прямую АВ. Точка пересечения прямой линии АВ с линией профиля является искомой точкой К, пересечения прямой с топографической поверхностью.

При построении профиля в свободном месте чертежа точки можно построить путем наложения полоски бумаги на план. Отметив их, затем перенести точки на линию условного горизонта. Наиболее часто эти задачи встречаются при проектировании дорог, трубопроводов и других сооружений.

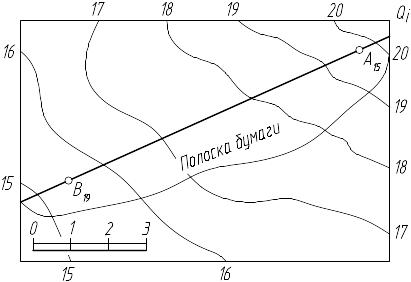
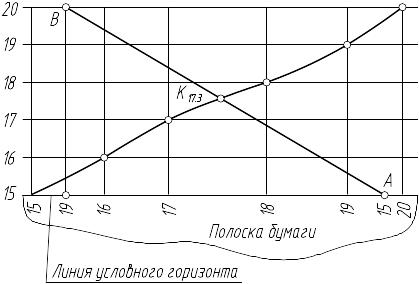
а) б)

Рисунок 7.47

16. Позиционные задачи на комплексном чертеже. Построение точек пересечения прямой с поверхностью.

Изображение геометрических тел с помощью горизонталей значительно упрощает построение сечений, так как любая линия сечения может быть выполнена как геометрическое место точек пересечения горизонталей с одинаковыми высотными отметками. На этом принципе выполнялось построение линии пересечения двух плоскостей. Поэтому, решая задачу пересечения гранных или кривых поверхностей плоскостью или прямой, необходимо в начале выполнить градуирование прямолинейных элементов этих поверхностей и построить горизонтали поверхности.