28. Стереографическая проекция
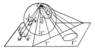
Стереографическая проекция, соответствие между точками сферы и плоскости, получаемое следующим образом: из некоторой точки С на сфере (центра С. п.) другие точки сферы проектируются лучами на плоскость, перпендикулярную радиусу сферы ОС и не проходящую через С (см. рис.; обычно эту плоскость проводят или через центр О сферы, или через точку С' — конец диаметра сферы СС'). При этом каждая точка М сферы, отличная от С, перейдёт в некоторую точку М' плоскости; такое соответствие (после исключения из сферы самого центра проекции С, которому никакая точка плоскости не соответствует) будет взаимно однозначным. Основные свойства С. п.: 1) окружностям на сфере соответствуют окружности же на плоскости (на рис. окружности Г соответствует окружность Г'), причём окружностям, проходящим через центр С. п., соответствуют на плоскости прямые линии (окружности бесконечно большого радиуса; на рис. у и у')', 2) соответствие, устанавливаемое С. п., является конформным, т. е. сохраняет углы (см.Конформное отображение), например, угол LMN на сфере равен углу L'M'N' на плоскости.
С. п. — перспективная картографическая проекция. Часто применяется в картографии, т.к. для территории округлой формы из всех равноугольных проекций даёт наименьшее колебание масштаба. Используется также в астрономии, кристаллографии и др.
*
*
*