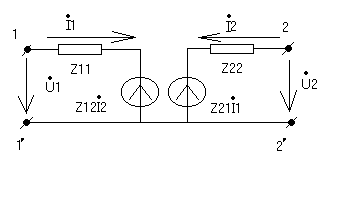
Схемы замещения индуктивно сведённых ветвей в z параметрах с управляемыми источниками.

ИНУТ

П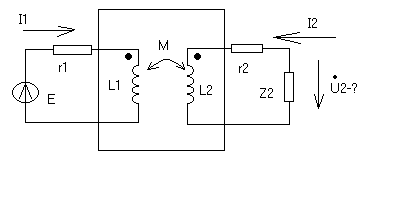 ример:

Известно: E,,r₁,r₂,Z₂, L₁, L₂, M

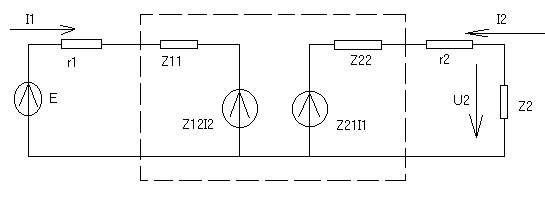
( II-ой закон Кирхгофа для катушек)

,

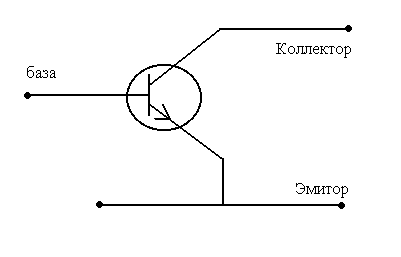
Транзистор. Биполярный n-p-n транзистор в минимальном режиме.

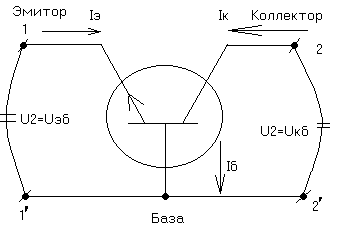
Физическая модель транзистора или модель Эберса-Мосла.

Рассмотрим малые сигналы, поэтому можно говорить, что транзистор в минимальном режиме.

Транзистор не взаимный элемент, т.к. он содержит управляемый источник тока, а управляемые источники тока независимы.

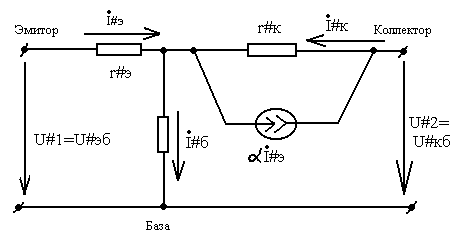
Найдём матрицу Z

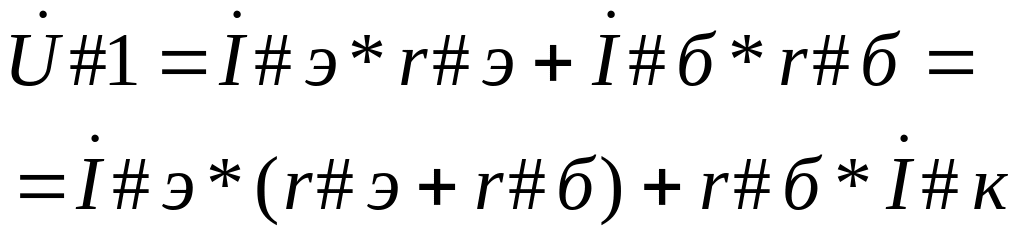
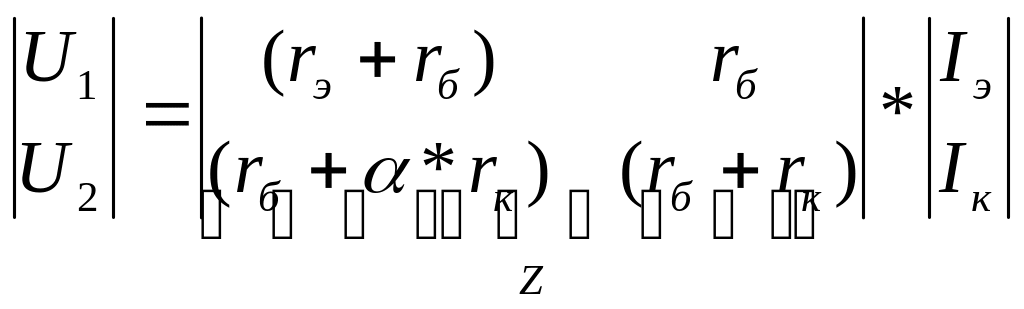
Модель транзистора с управляемыми источниками в н параметрах.

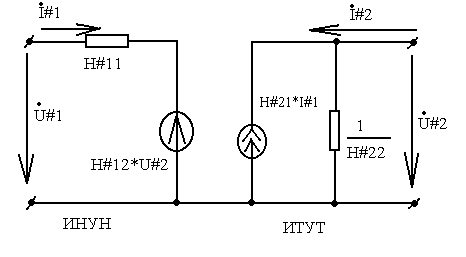
1) Входное сопротивление

Zвх (j)=r+j**L-j/(*c)

Zвх (j_)=r+j*_*L-j/(_*c)

Послед _*L= 1/(_*c)

Ur=I*r Uc=-j*I*1/(_*c) UL=I*j*_*L

-Uc= UL

Uвх= Ur

2) Добротность RLC- контура

_*L)/r=L/(r*((L*C)^1/2))=(1/r)*((L/C)^1/2)=Q-добротность

1/(_*c*r)= ((L*C)^1/2)/(r*c)= ((L/C)^1/2)/r=Q _=1/((L*C)^1/2)

Q=_*L)/r=1/(_*c*r)

Zвх (j)=r+j(*L-1/(*c))=r+ j*_*L(/_ - _/)=r(1+j**_*L)/r)= =r(1+j*Q*)

-расстройка

Передаточная ф-я последовательной RLC –цепи.

а) Каноническая форма записи передаточной ф-ии 2-го порядка.

H(p)=(b₂*p²+b₁*p+b₀)/(p²+(_/Q)*p+²_) –общий кан. вид перед. ф-ии.

б) Последовательная схема

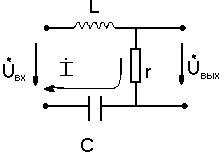для этой схемы определим передаточную ф-ю

H(j)=(U_вых)/(U_вх)=(I*r)/(I*Z_вх (j))

H(p)=r/(Z_вх (p))=r/(r+p*L+1/(p*c)) = (r*p*c)/(p²*L*c+p*r*c+1)=(*)

Z_L=j**L=p*L

Z_c=1/(j**c)=1/(p*c) R/L=(_*r)/(_*L)=_/Q

(*)=(p*r/L)/(p²+p*r/L+1/(L*C))=(p*_/Q)/(p²+(_*p)/Q+²_)

H(j)=(j*_/Q))/(²_-²)+j**_/Q)) – передаточная функция, записанная через 

АЧХ

| H(j)|= H()=(*_/Q))/

ФЧХ

arctg((*_)/(Q*(²_-²))

H (Q1 Q2

Hmax Hm/((2)^1/2)

0 max  

Q2>Q1



 

 



 

 

 

ППФ

 __H(_))/H(_))=H(_))/H(_))=1/(2)^1/2 Q=(_)/(

Чем уже полоса пропускания, тем больше добротность поля.

2)

H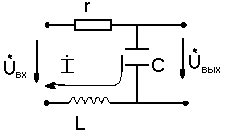 (p)=(U_вых(p))/(U_вх(p))=(I*Z_c)/(I*Z_вх)=(1/(p*c))/(r+p*L+1/(p*c))=1/(p²*L*C+p*c*r+1)= =(1/(L*c))/(p²+p*(r/L)+1/(L*c))=(^_)/(p²+_Q)*p+^_)

H(j=(^_)/((^_-²)+_Q)*p)

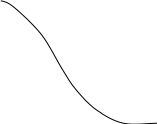
АЧХ

|H(j)| = H()=(²₀)/((²_-²)²+(*_/Q))²)^1/2

ФЧХ

0arctg((*_)/(Q*(²_-²))

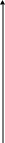
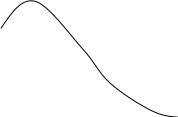
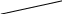H(Q>1/(2^1/2)

 

 



Q<1/(2^1/2) ФНЧ

_max=_Q²))^1/2

 

max 0



 0 

 

 



H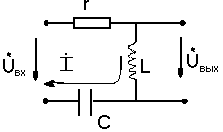 (p)=(U_вых(p))/(U_вх(p))=(I*ZL)/(I*Z_вх)= =(p*L)/(r+p*L+1/(p*c))=(p²*L*C)/(p²*L*C+p*c*r+1)= =p²/p²+Q)*p+^_)

H(j=(-²)/((^_-²)+j*_Q)*)

arctg((*_)/(Q*(²_-²))

ФВЧ

_квазирезонансная частота

_max=_

  Q>1/(2^1/2)

 

 

 

Q<1/(2^1/2)

  max 







0. 



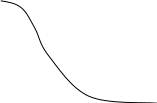
4) полосно-заграждающий фильтр



 

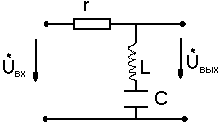
 /(2^1/2)



Вид фильтра 

__-полоса заграждения

НЧ H(p)=H₀*^_/(p²+Q)*p+^_

ВЧ H(p)=H₀*p²/(p²+Q)*p+^_)

ПП H(p)=H_max*p/(p²+Q)*p+^_)

ПЗ H(p)=H₀*(p²+^₁)/(p²+_Q)*p+^_)

=₀

z_вх(j=r+jL-j*1/(c)

z_вх(j₀)=r+j₀L-j*1/(₀*c)=r

послед. ₀*L=1/(₀*c)

_r= *r ; _c=-j* *1/(₀*c); _L=I*j*₀*L

- _c= _L; _вх=U_r