Эквивалентная схема многополюсных электрических источников.

I. Управляемые источники.

1) Источник напряжения, управляемые током (ИНУТ).

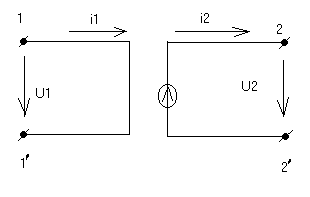e₂=Z₂₁*i₁ (ИНУТ)

U₁=0 (короткое замыкание)

U₂=e₂=Z₂₁*i₁

DetZ=0, следовательно Y= (не будет)

2) Источник тока, управляемый напряжением (ИТУН)

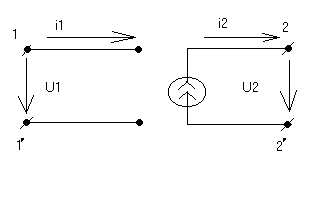J₂ = g₂₁*U₁

i₁=0 - разомкнут

i₂=J₂=g₂₁*U₁

Y =

detY=0 следовательно Z – не существует

3) Источник тока управляемый током (ИТУТ)

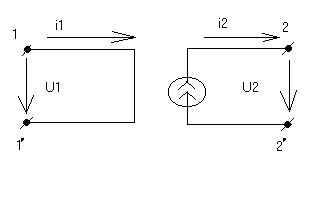
J₂=kⁱ₂₁*i₁

U₁=0 – замкнута

i₂= J₂= kⁱ₂₁*i₁

H =

4) Источник напряжения управляемый напряжением (ИНУН)

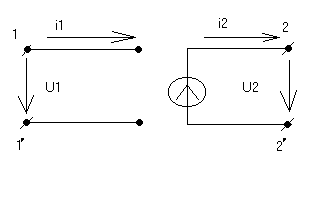
e₂=k^u₁₂*U₁

i₁=0

U₂=e₂=k^u₂₁*U1

Существует только коэф передачи по напряжению. Нет матриц Y, Z, H

Входная ветвь (11^’) называется управляющей. Выходная ветвь (22’)называется управляемой. Являются не взаимными 4-ч полюсниками.

Схема замещения n-полюсников с управляемыми источниками.

Индуктивно связаные ветви

Индуктивно связанные ветви – две или более ветвей (катушек индуктивности) сцеплённых общим магнитным потоком.

L ₁-первичная, L₂ вторичная индуктивная обмотка.

M – взаимная индуктивность первичной вторичной обмоток.

M>0 при согласном включении обмоток, токи входят в одноименные зажимы соноправленно.

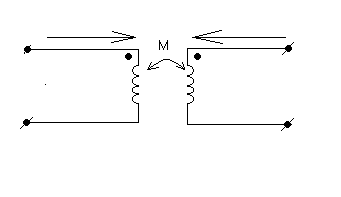
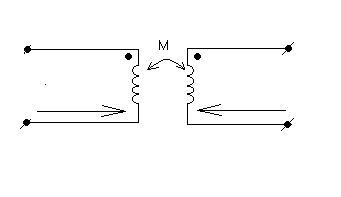
или

M<0 при встречном включении, токи входят в разноименные зажимы.

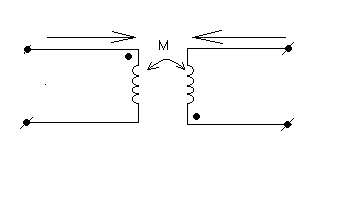
Запишем II закон Кирхгофа для первичной и вторичной обмотки.

для 1-ой обмотки

для 2-ой обмотки

Будем считать что токи, магнитные потоки и напряжение изменяются по одному гармоническому закону, тогда запишем эти уравнения в комплексной плоскости:

Z₂₁=Z₁₂ получим, что индукции сведённых ветвей имеют взаимную матрицу.