- •Определение электрической цепи
- •Математическая модель электрической цепи
- •Математические модели двуполюсных элементов цепи во временной области.
- •П I(t) ассивные элементы цепи:
- •Реальный конденсатор
- •Преобразование источника тока в эдс и обратно.
- •Топологические матрицы и матричные уравнения электрических цепей Граф электрической цепи и его основные подграфы.
- •Топологические матрицы
- •Контурная матрица
- •Закон Ома в матричном виде
- •Обобщенная ветвь электрической цепи (Закон Ома для обобщенной ветви)
- •Баланс мощностей
- •Узловое уравнение цепи. Метод узловых потенциалов.
- •Составление узловых ур-ний непосредственно по схеме.
- •Анализ эл. Цепей в частотной области. Синосоидальные источники. Установившиеся режимы.
- •Метод комплексных амплитуд.
- •Переход из временной области на комплексную и обратно.
- •Преобразование электрического сигнала во временной и частотной областях.
- •Расчет цепей с несинусоидальными периодическими источниками
- •Модели двухполюсных элементов в частотной области
- •Законы Кирхгофа в комплексной форме.
- •Комплексно-символьный метод расчета электрических цепей синусоидального тока и напряжения
- •Комплексное сопротивление и проводимость
- •Основные теоремы и принципы расчета цепей синусоидального тока и напряжения.
- •Мощность цепи синусоидального тока и напряжения.
- •Баланс мощности в цепи синусоидального тока и напряжения.
- •Ч етырёхполюсные элементы их матрицы и уравнения.
- •Определение коэффициентов четырехполюсников.
- •Соединения четырехполюсников.
- •1) Последовательное
- •2) Параллельное
- •3) Каскадное
- •Эквивалентная схема многополюсных электрических источников.
- •I. Управляемые источники.
- •Индуктивно связаные ветви
- •Схемы замещения индуктивно сведённых ветвей в z параметрах с управляемыми источниками.
- •Транзистор. Биполярный n-p-n транзистор в минимальном режиме.
- •Физическая модель транзистора или модель Эберса-Мосла.
- •Модель транзистора с управляемыми источниками в н параметрах.
- •Добротность r-l-c контура
- •Предаточная функция последовательной r-l-c цепи
- •Коммутация
- •Идеальный ключ (_/ _)
- •Законы комутации.
- •Модели источников и единичная функции.
- •Классический метод рассчета переходных процессов.
- •Разряд конденсатора.
- •Воздействие прямоугольного импульса.
- •Переходные процессы в r-l цепи.
- •Порядок расчёта разветвлённой цепи 1-ого порядка.
- •Переходные процессы в последовательной r-l-c цепи.
- •Апериодический заряд конденсатора – когда корни действительные и разные.
- •Апериодический, критический заряд конденсатора.
- •Составление и решение уравнений состояния.
- •Правила определения н1 и н2:
- •Уравнения состояния. Определение начальных условий.
- •Решение уравнений состояния для случая постоянных источников эдс и тока.
- •Переходные процессы (динамические режимы) в цепях синусоидального тока и напряжения.
- •Экзаменационная программа по курсу “Электротехника и Электроника”.
Баланс мощности в цепи синусоидального тока и напряжения.
A![]() =0;
A
=0
=0;
A
=0
=Aт*φ;
![]() *
B
=φт*A*
B
=0
*
B
=φт*A*
B
=0
![]() в
в
![]()
S ̃=
̃=![]() *
k
*
k
![]() S̃k=0
Сумма комплексных мощностей всех
ветвей схемы равна нулю
S̃k=0
Сумма комплексных мощностей всех
ветвей схемы равна нулю

* =0 - теорема Теллегена
Докажем что сумма мощностей отдаваемая источниками равна сумме мощностей потребляемых цепью.
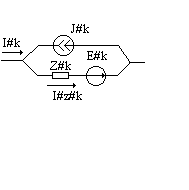
k=
zk-![]()
![]() =
zk*zk-
=
zk*zk-![]()
Uk*
k=Uk*(![]()
![]()

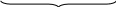
S̃потр. S̃ист.
S̃E
=![]() S̃J=
S̃J=
![]()
S̃потр=(r+jx)*
![]() =r*
+jx*
=Pпотр+jQпотр
=r*
+jx*
=Pпотр+jQпотр
S̃ист=Pист+jQист

S̃ист= S̃потр Баланс мощности
Передача
мощности от активного двухполюсника
к п ассивному
в цепях синусоидального тока и напряжения.
ассивному
в цепях синусоидального тока и напряжения.
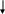 I
zвх
I
zвх


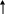
 U
.
zн=R+jx
U
.
zн=R+jx
A П Ep
Zвх=rвх+jxвх
Zн=rн+jxн
P=zн*![]() ;
=
;
=

Максимальная мощность:
1)
xн= -xвх
;
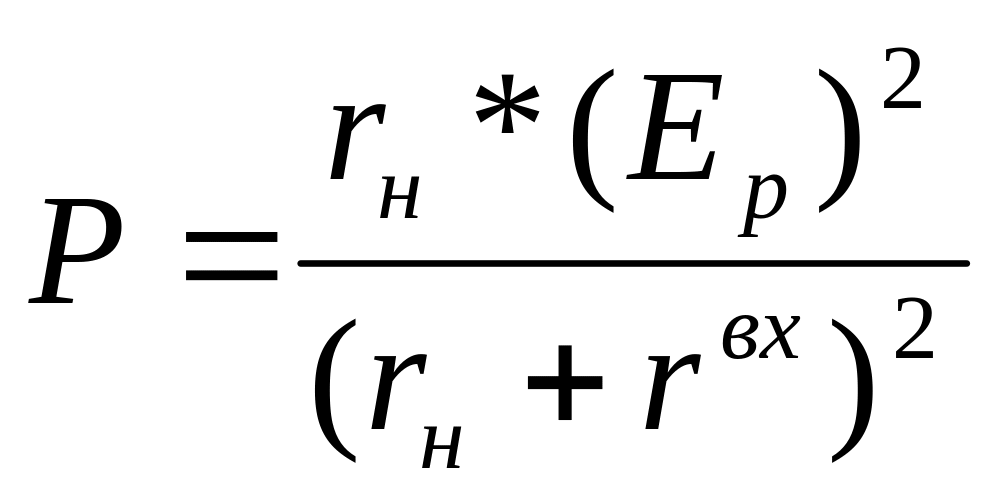
 2) rн=rвх
; zн=rвх-jxвх
2) rн=rвх
; zн=rвх-jxвх
Пример:
 r
r

 U(t)
U(t)
i(t) L

C
U(t)=10*sin(104*t) B
ω=104 рад/с ω=2πf
r=10 Ом ; C=0.5*10-5 Ф
i(t), rвх - ?
Используем метод комплексных амплитуд:
U
(t)
U=![]()
Zвх=r+jωL-j/(ωC)=r+zL+zC
ZL=jωL=10j Ом
ZC= -j/(ωC)= -20j Ом
Zвх=10+10j-20j=10-10j
10 -10j Характер активно-емкостной

I
 =U/zвх=
=U/zвх=![]()
Ч етырёхполюсные элементы их матрицы и уравнения.
Схемы трехполюсников, рассмотренные как четырехполюсники
с одним зажимом
4-х полюсник ‘I’1
‘I’2
‘I’1
‘I’2

 1
2
1
2
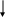
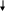 ‘U’1
‘U’2
‘U’1
‘U’2
1 ’
2’
’
2’
Определение коэффициентов четырехполюсников.
1) Уравнение типа “Z” (Z=[Ом])
 Z11
Z12
Z11
Z12
‘U’1=Z11’I’1+Z12’I’2 Z=
‘U’2=Z21’I’1+Z22’I’2 Z21 Z22
П усть
сначала ‘I’2=0
(разомкнуты 2, 2’)
усть
сначала ‘I’2=0
(разомкнуты 2, 2’)
Z11=’U’1\’I’1 ||’I’2=0 –входное сопротивление при разомкнутых выходных зажимах.
Z21=’U’2\’I’1 ||’I’2=0 –взаимное сопротивление при разомкнутых выходных зажимах.
П усть ‘I’1=0 (разомкнуты 1, 1’)
Z22=’U’2 \’I’2 ||’I’1=0 –выходное сопротивление при разомкнутых входных зажимах.
Z12=’U’1\’I’2 ||’I’1 =0 –взаимное сопротивление при разомкнутых входных зажимах.
2) Уравнение типа “Y” (Y=[См])
‘I’1=Y11’U’1+Y12’U’2
‘I’2=Y21’U’1+Y22’U’2

Y11 Y12
Y=
Y21 Y22
3
![]()
![]()





 1
2
1
2
 ‘U’1=H11’I’1+H12’U’2
‘U’1=H11’I’1+H12’U’2
 ‘I’2=H21’I’1+H22’U’2
‘I’2=H21’I’1+H22’U’2
![]()
![]()
1’ 2’
Пусть сначала ’U’2=0
H11=’U’2\’I’1 ||’U’2=0 – входное сопротивление четырехполюсника при закороченных выходных зажимах.
H21=’I’2\’I’1 ||’U’2=0 – коэффициент передачи по току при закороченных выходных зажимах.
H22=’I’2\’U’1 ||’I’2=0 – выходная проводимость при разомкнутых входных зажимах .
H12=’U’1\’U’2 ||’I’1=0 – коэффициент передачи по напряжению при разомкнутых входных зажимах.
4) Уравнение типа “A”
‘U’1=A’U’1+B’I’2
‘

 I’1=C’U’2+D’I’2
‘I’1
‘I’2
I’1=C’U’2+D’I’2
‘I’1
‘I’2
A B
A=
C D
Условия взаимности для линейных пассивных четырехполюсников:
1) Z12=Z21 3) H12= --H21
2) Y12= Y21 4) AD—BC=1
Условия симметричности 2-ух четырехполюсников.
1) Z11= Z22 3) H11 H22—H21 H22=1
2) Y11= Y22 4) A=D
Замечание
Если в 4-x полюснике есть источники (активные элементы), то ур-ние можно записать в следующем виде:
![]()
В общем случае четырехполюсник имеет 4 независимых параметра. Взаимный имеет 3 параметра. Взаимо-симметричный—2 независимых параметра.
Схемы замещения четырехполюсников.
1) T-образная схема.
‘I’1
‘I’2



‘ U’1 Z1 Z2 ‘U’2
 Z3
Z3

взаимный четырехполюсник
Н айдем Z для T образной схемы.
‘U’1=Z11’I’1+Z12’I’2
‘U’2=Z21’I’1+Z22’I’2
Пусть 2. 2’ разомкнуты -‘I’2=0
Z11=’U’1\’I’1 ||’I’2=0 –входное сопротивление
Z 21=’U’2\’I’1
||’I’2=0=(’I’1
Z3)\ ’I’1=Z3
21=’U’2\’I’1
||’I’2=0=(’I’1
Z3)\ ’I’1=Z3
Пусть ‘I’1=0 (разомкнуты 1, 1’) Z12=Z21 взаимный четырехполюсник
Z22=’U’2 \’I’2 ||’I’1=0 –выходное сопротивление
Z12=’U’1\’I’2 ||’I’1 =0=(’I’2 Z3)\ ’I’2=Z3
2) П-образная схема.
‘ I’1 ‘I’2


 Z1
Z1
 ‘U’1
Z2 Z3
‘U’2
‘U’1
Z2 Z3
‘U’2
 ‘U’1=H11’I’1+H12’U’2
‘U’1=H11’I’1+H12’U’2
‘I’2=H21’I’1+H22’U’2
Проведем опыт К.З. на входе --’U’2=0
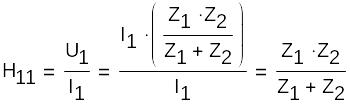
![]()
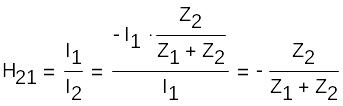
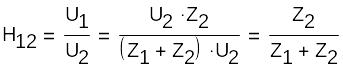
![]()