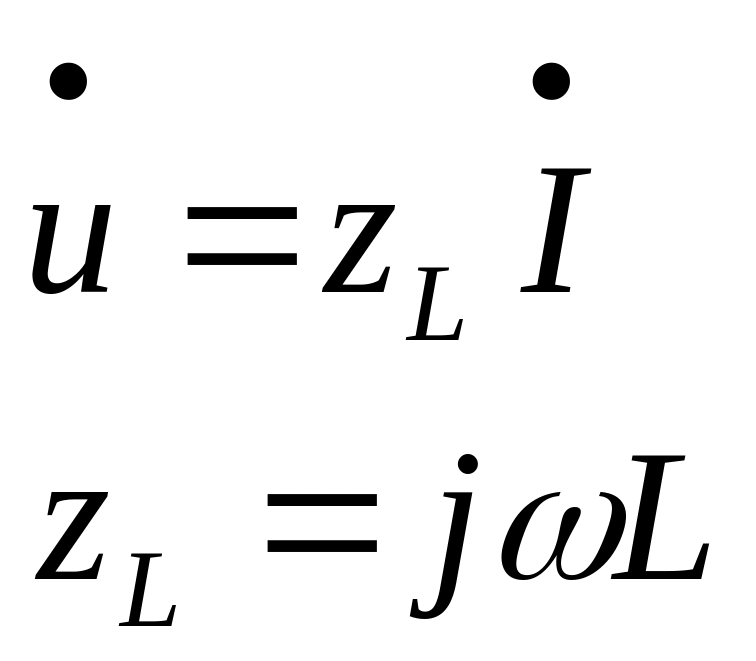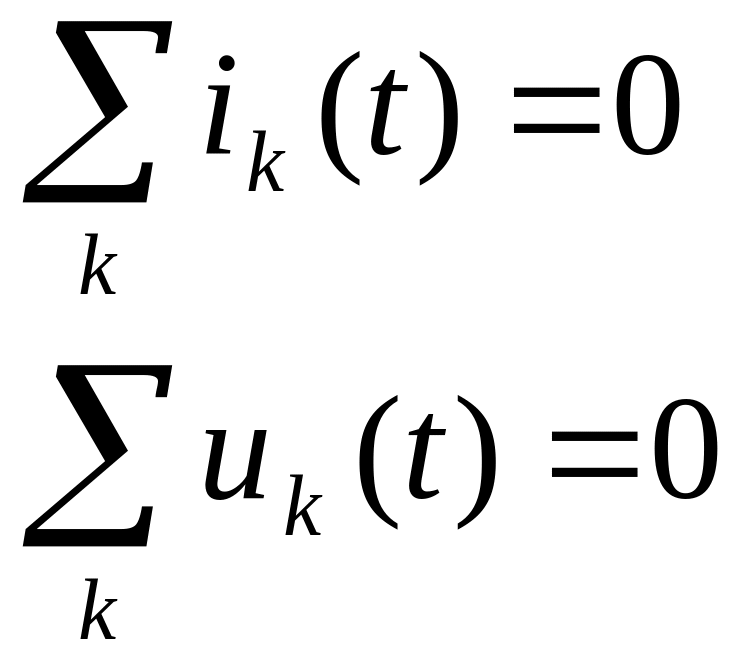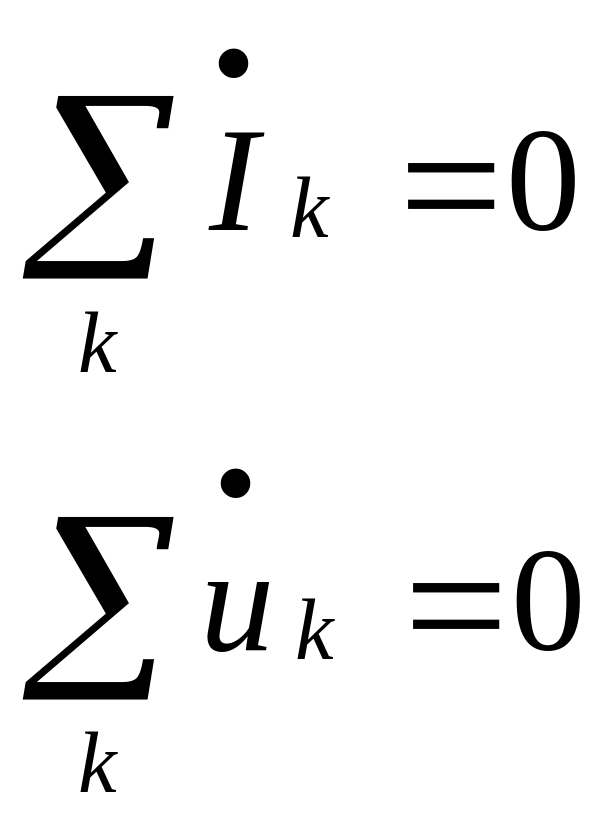- •Определение электрической цепи
- •Математическая модель электрической цепи
- •Математические модели двуполюсных элементов цепи во временной области.
- •П I(t) ассивные элементы цепи:
- •Реальный конденсатор
- •Преобразование источника тока в эдс и обратно.
- •Топологические матрицы и матричные уравнения электрических цепей Граф электрической цепи и его основные подграфы.
- •Топологические матрицы
- •Контурная матрица
- •Закон Ома в матричном виде
- •Обобщенная ветвь электрической цепи (Закон Ома для обобщенной ветви)
- •Баланс мощностей
- •Узловое уравнение цепи. Метод узловых потенциалов.
- •Составление узловых ур-ний непосредственно по схеме.
- •Анализ эл. Цепей в частотной области. Синосоидальные источники. Установившиеся режимы.
- •Метод комплексных амплитуд.
- •Переход из временной области на комплексную и обратно.
- •Преобразование электрического сигнала во временной и частотной областях.
- •Расчет цепей с несинусоидальными периодическими источниками
- •Модели двухполюсных элементов в частотной области
- •Законы Кирхгофа в комплексной форме.
- •Комплексно-символьный метод расчета электрических цепей синусоидального тока и напряжения
- •Комплексное сопротивление и проводимость
- •Основные теоремы и принципы расчета цепей синусоидального тока и напряжения.
- •Мощность цепи синусоидального тока и напряжения.
- •Баланс мощности в цепи синусоидального тока и напряжения.
- •Ч етырёхполюсные элементы их матрицы и уравнения.
- •Определение коэффициентов четырехполюсников.
- •Соединения четырехполюсников.
- •1) Последовательное
- •2) Параллельное
- •3) Каскадное
- •Эквивалентная схема многополюсных электрических источников.
- •I. Управляемые источники.
- •Индуктивно связаные ветви
- •Схемы замещения индуктивно сведённых ветвей в z параметрах с управляемыми источниками.
- •Транзистор. Биполярный n-p-n транзистор в минимальном режиме.
- •Физическая модель транзистора или модель Эберса-Мосла.
- •Модель транзистора с управляемыми источниками в н параметрах.
- •Добротность r-l-c контура
- •Предаточная функция последовательной r-l-c цепи
- •Коммутация
- •Идеальный ключ (_/ _)
- •Законы комутации.
- •Модели источников и единичная функции.
- •Классический метод рассчета переходных процессов.
- •Разряд конденсатора.
- •Воздействие прямоугольного импульса.
- •Переходные процессы в r-l цепи.
- •Порядок расчёта разветвлённой цепи 1-ого порядка.
- •Переходные процессы в последовательной r-l-c цепи.
- •Апериодический заряд конденсатора – когда корни действительные и разные.
- •Апериодический, критический заряд конденсатора.
- •Составление и решение уравнений состояния.
- •Правила определения н1 и н2:
- •Уравнения состояния. Определение начальных условий.
- •Решение уравнений состояния для случая постоянных источников эдс и тока.
- •Переходные процессы (динамические режимы) в цепях синусоидального тока и напряжения.
- •Экзаменационная программа по курсу “Электротехника и Электроника”.
Расчет цепей с несинусоидальными периодическими источниками
![]()
![]()
При подаче на вход периодической синусоидальной функции:
Раскладываем в ряд Фурье.
Рассчитываем схему по принципу суперпозиций, т. е.
 .
Расчет комплексным методом:
.
Расчет комплексным методом:
![]()

 Е
Е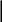
 сли
источники представить в ряд Фурье, то
в расчете можно использовать принцип
суперпозиций. Отдельно взятая гармоника
рассчитывается с помощью метода
комплексных амплитуд.
сли
источники представить в ряд Фурье, то
в расчете можно использовать принцип
суперпозиций. Отдельно взятая гармоника
рассчитывается с помощью метода
комплексных амплитуд.
Комплексная форма ряда Фурье:
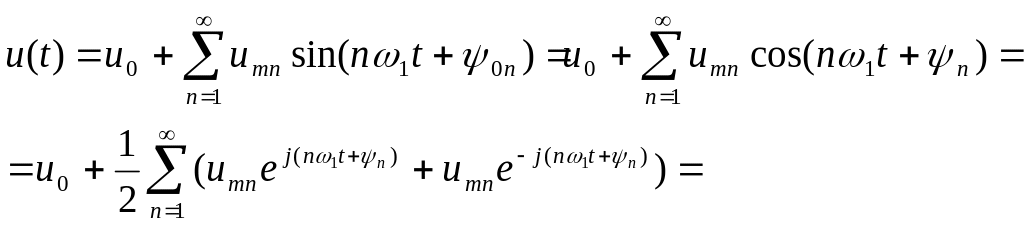
![]()
![]()
![]()
![]()
 (2)
(2)
![]() - комплексная амплитуда
- комплексная амплитуда
![]() гармоники
гармоники
![]()
![]() - комплексно сопряженная
амплитуда
гармоники
- комплексно сопряженная
амплитуда
гармоники
![]()
Можно найти комплексное максимальное значение:
![]()
Действующее значение
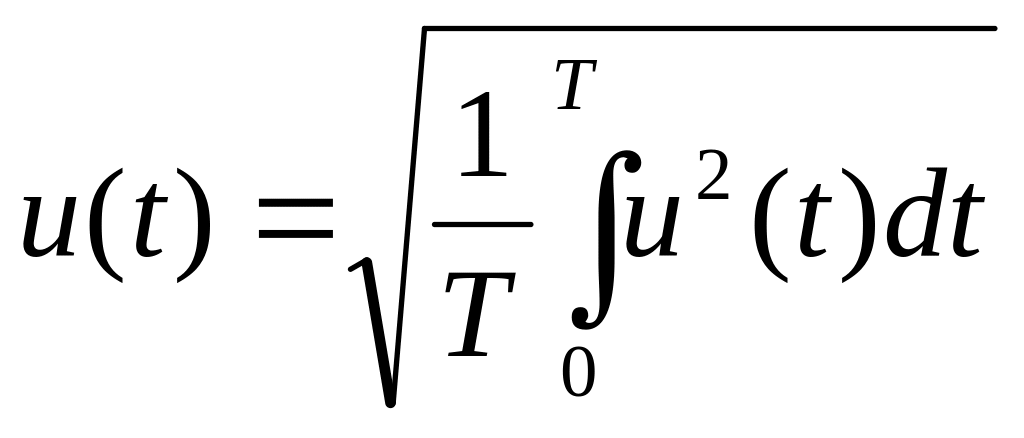
![]() - во временной области
- во временной области
![]() - в частотной области
- в частотной области
![]() - действующее значение
- действующее значение
![]()
Если
![]() ,
то
,
то
![]() .
.
Если
![]() ,
то
,
то
 .
.
Модели двухполюсных элементов в частотной области

![]() (2)
(2)

![]() (3)
(3)
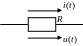
Резистивный элемент:
![]()
![]()
![]()
 На
резистoре не происходит
изменение фазы
На
резистoре не происходит
изменение фазы
![]()
![]()

И
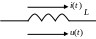 ндуктивный
элемент:
ндуктивный
элемент:
![]()

![]()
![]() - комплексное сопротивление
индуктивного элемента
- комплексное сопротивление
индуктивного элемента
![]()
![]()
![]()
![]() ,
где
,
где
![]() - сопротивление индуктивного элемента
- сопротивление индуктивного элемента
![]()
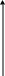

 Вектор напряжения
опережает ток на 900
Вектор напряжения
опережает ток на 900





К
 онденсатор
(емкость):
онденсатор
(емкость):
![]()


![]() - комплексное сопротивление
конденсатора
- комплексное сопротивление
конденсатора

![]() ,
где
,
где
![]() - сопротивление конденсатора
- сопротивление конденсатора
![]()

Напряжение на емкости отстает от тока на 900
Введем
![]() - комплексная проводимость:
- комплексная проводимость:
|
|
|
|
|
|
|
|
|
|
|
|
Законы Кирхгофа в комплексной форме.
![]()
![]()
Комплексно-символьный метод расчета электрических цепей синусоидального тока и напряжения
Во временной области |
В частотной области |
|
|
|
|
|
|
Комплексное сопротивление и проводимость
Рассмотрим пассивный двухполюсник:
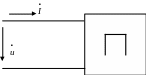
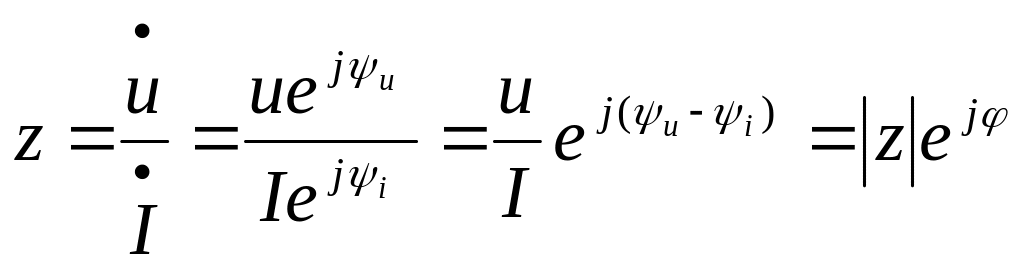 ,
где
,
где
![]() - модуль входного комплексного
сопротивления,
- модуль входного комплексного
сопротивления,
![]() - аргумент комплексного сопротивления
- аргумент комплексного сопротивления
![]()
![]() ,
где
,
где
![]() - активное сопротивление,
- активное сопротивление,
![]() - реактивное сопротивление
- реактивное сопротивление
С![]() хемы
замещения пассивных двухполюсников:
хемы
замещения пассивных двухполюсников:
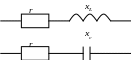
![]()
- комплексная проводимость
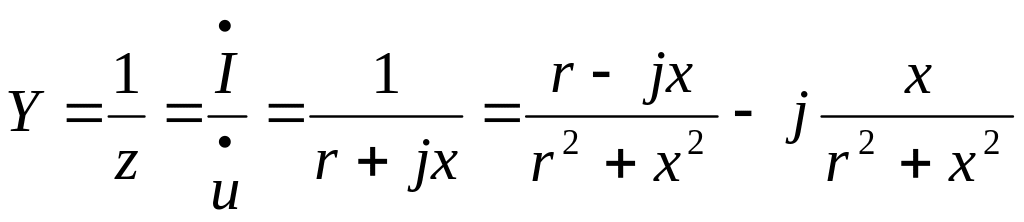
![]() ,
где
,
где
![]() - активная проводимость,
- активная проводимость,
![]() - мнимая проводимость
- мнимая проводимость
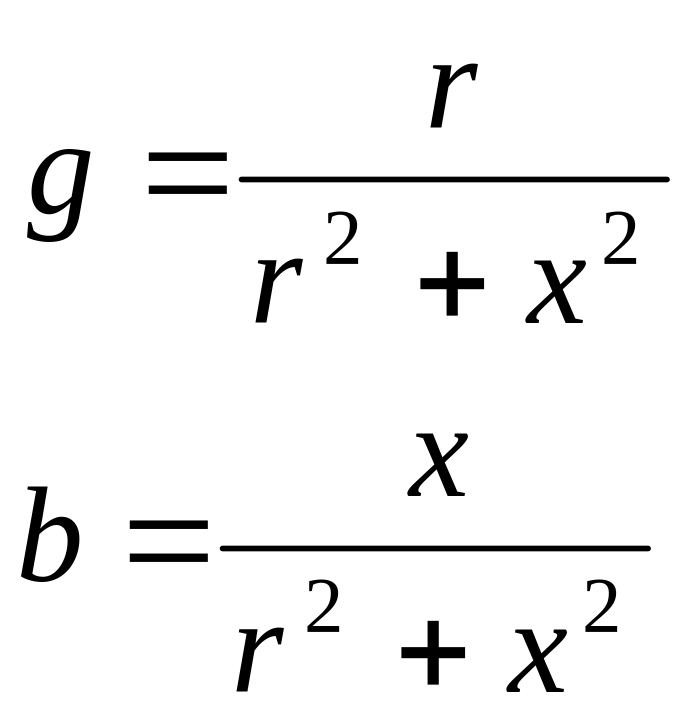
Схемы замещения пассивных двухполюсников:


Основные теоремы и принципы расчета цепей синусоидального тока и напряжения.
Законы Кирхгофа:
. .
AIв=0 –1й закон BUв=0 – 2й закон
принцип суперпозиции:
Ток в любой ветви линейной схемы равен алгебраической сумме от действия каждого источника в отдельности:
r → Z=r±jx
g → У=g±jb
![]()
Метод эквивалентного генератора или активного двухполюсника:
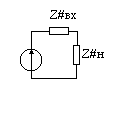
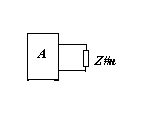
Zвх=rвх±jxвх
Zн=rн±jxн
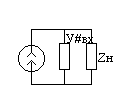
Увх=1/zвх
Метод узловых потенциалов:
Yу*φ=Jу
Yу=A*Yв*Aт ---- матрица узловых проводимостей
Jу=A*J-A*Yв*Eв
Мощность цепи синусоидального тока и напряжения.
Мгновенная мощность:
P(t)=U(t)*i(t)
U(t)=Umax*sin(ωt+ψu)
i(t)=Imax*sin(ωt+ψi)
P(t)=Umax*Imax*sin(ωt+ψu)*sin(ωt+ψi)=![]() *[cos(ψu-
ψi)-cos(2ωt+
ψu+
ψi)]
*[cos(ψu-
ψi)-cos(2ωt+
ψu+
ψi)]
ψu - ψi=φ
А ктивная
мощность - средняя за период.
0
ктивная
мощность - средняя за период.
0
P=![]()
=
![]()
![]()
P=U*I*cos(φ) [Вт]
Реактивная мощность:
Q=U*I*sin(φ) [ВАР] – вольт-ампер реактивная
Комплексная мощность:
S̃=
*![]() =U*ejψu
* I * e-jψI=U*I*ej(ψu
- ψI)=U*I*ejφ=
=U*ejψu
* I * e-jψI=U*I*ej(ψu
- ψI)=U*I*ejφ=
=U*I*cos(φ)+j*U*I*sin(φ)=P+jQ
S̃=[Вольт Амперы]
S – полная мощность
S=![]() =UI
=UI
Рассмотрим z=r±jx
Если
z=r, тогда
P=![]()
Если
z=jx, тогда
P=0; S̃=P+jQ=jωL![]()
ZL → Q>0
Если
z=-jx, тогда
P=0; S̃=-j*![]()
ZC → Q<0