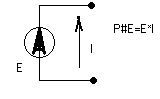
Баланс мощностей

Баланс мощностей - ∑ мощностей, отдаваемых источниками равна ∑ мощностей, потребляемых резисторами.

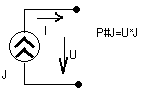
(одна клема-i, другая-j)

I_k=I_Rk-J_k; U_k=R_k*I_Rk -E_k;

U_k*I_k=U_k*(I_Rk -J_k)=R_k*(I_Rk)²-E_k*I_Rk-U_k*J_k;

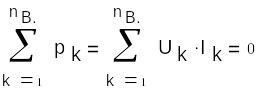
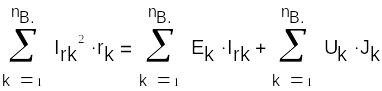
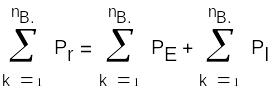
Узловое уравнение цепи. Метод узловых потенциалов.

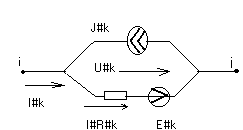
I_{r k}=(U_Rk)/R_k=U_Rk*g_k; где g_k=1/R_k- проводимость

I_Rk=(U_k+E_k)/R_k=(_i-_j-E_k)/R_k ;

A * I =0 (1 закон Кирхгофа);

I^B=G^B*U_R^B-J^B=G^B*(U^B + E^B)-J^B ; U_R= U^B + E^B

A *G^B*U^B+ A *G^B*E^B- A *J^B=0 ;

U^B=A^T*=G^B*(A^T*+ E^B)- J^B домножим на A

A * I^B = A *G^B* A ^T*+ A *G^B*E^B- A *J^B

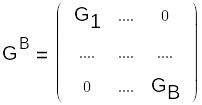
В-ветви; У-узлы; G *=J узловое уравнение в матричном виде.

Замечание: Метод узловых потенциалов справедлив для схем в которых отсутствуют схемы с проводимостью равной нулю, т.е. нет короткозамкнутых цепей (g_i=, т.е. r_i=0)

Число ур-ний n_y-1<n_B

Составление узловых ур-ний непосредственно по схеме.

Из ур-ния G *= J можно посчитать =J^y/G^y

i j

k

n_в-число вершин

A = = [Разобьем матрицу на подматрицы] = | A ₁, A ₂ ….. A _{n в}|

G ^У = A * G ^В*A ^Т= A ₁* A ₂*…* A _{n в} * * =

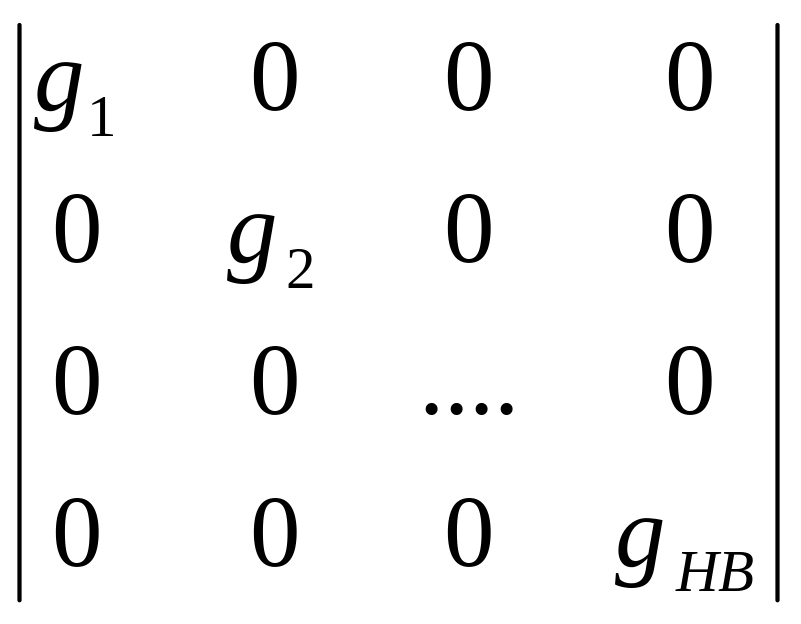= A ₁*g₁* A ₂*g₂*…* A _{n в}*g_{n в} * =

= A ₁*g₁* A ^T₁+ A ₂*g₂* A ^T₂+….+ A _{n в}*g_{n в}* A ^T_nв = A _K*g_K* A ^T_K ;

A _K*g_K* A ^T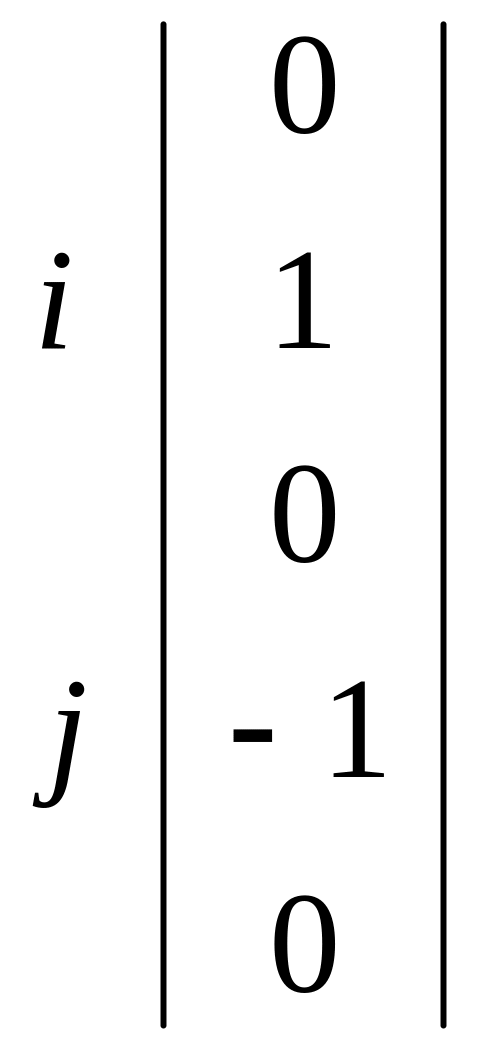_K= *g_K* =

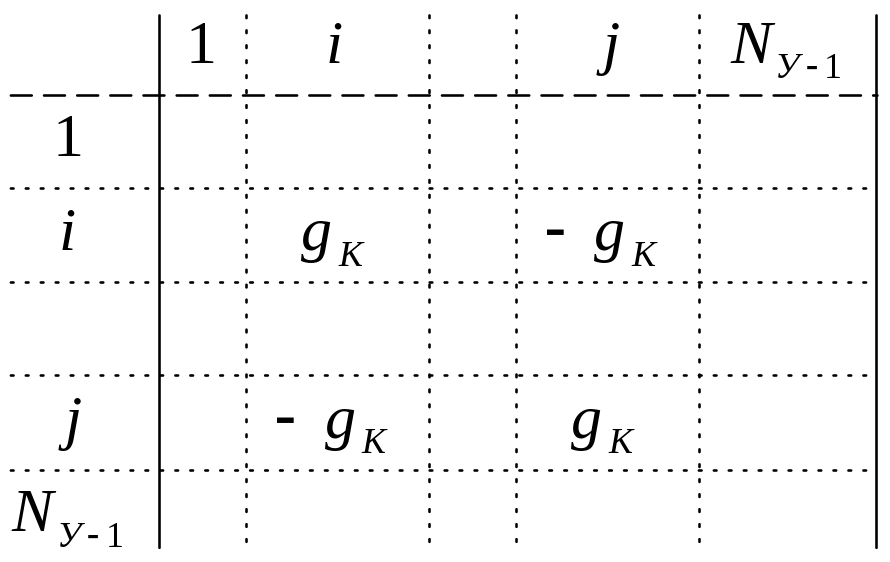
G ^У= ;g_ij-сумма проводимостей всех ветвей, подключенных к i-ому узлу, этот элемент всегда записывается со знаком ”+” ( ij-индексы при g^У)

g_ij- сумма проводимостей ветвей, соединены i-й и j-й узлы – знак “-”

g_ij=g_ii

J ^У= A * J ^В – A * G ^B*E^B =

N_y =4 ; φ₀ =0;

* =

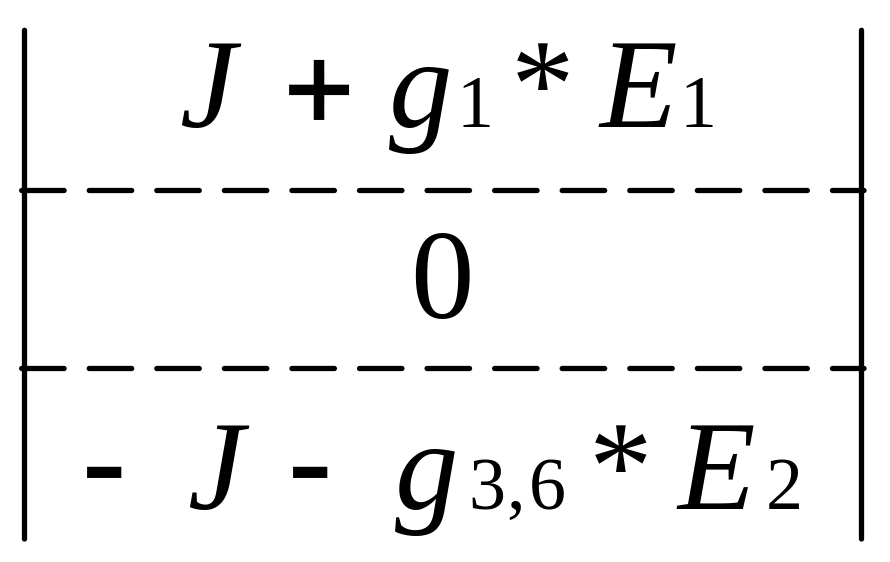= ; I₁=(ψ₀ - ψ₁ + E₁)*g₁; I₂=(ψ₂ – ψ₀)* g₂; и т.д.

Анализ эл. Цепей в частотной области. Синосоидальные источники. Установившиеся режимы.

Рассмотрим установившийся режим при включенных синусоидальных источниках.

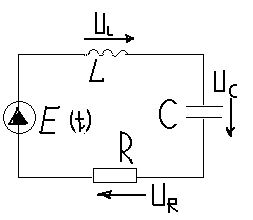
E(t)=U_L(t) + U_C(t) +U_R(t);

U_R(t)=R*I(t); U_L(t)= L* ; U_C(t)= ; i_c=c

R*I(t) + L* + = E(t) ;

R * + + = ; +

Метод комплексных амплитуд.

e^jψ= cosψ + j sinψ ; j ; j² =-1;

cos ψ = ; sin ψ = ;

I(t) = I_max * cos(ωt +ψ) = I_max *[e ^j(ωt+ψ) + e ^-j(ωt+ψ)] = *[I_max*e^jψ e^jωt +

+ I_max*e^-jψ*e^-jωt ] = [ _max *e^jωt + _max *e ^(-jωt)] = Re( _max *e^jωt) ;

_max – комплексная амплитуда тока =I_max * e^jψ ;

_max – комплексно - сопряжённая амплитуда = I_max * e^-jψ ;

_max * _max =I_max²=I_max²; I_max=I_max*e^j; I_max-модуль комплексной амплитуды тока.

-фаза, аргумент комплeксной амплитуды.

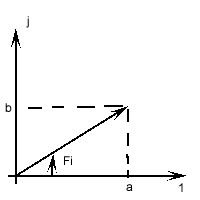
Если во временной области ток задан выражением i(t)=I_max*cos(t+)=I_max *sin(t+), то частотные области этот ток записывают так _max =I_max*e^j; i(t) соответствует _max. _max =I_max*cos+j*I_max*sin=a+j*b

Переход из временной области на комплексную и обратно.

U(t) =U_max*sin(ωt+ψ); _max=U_max*e^jψ ;

_max =I_max* e^jψ= I_max*cosψ + j*I_max*sinψ =a + j* b;

= a + j * b = C * e^jψ; C= ; ψ = arctg ;

Преобразование электрического сигнала во временной и частотной областях.

- зависимость напряжения от времени. С помощью преобразования Фурье можно перейти в частотную область. Функцию можно разложить в ряд Фурье, если она отвечает условию Дирихле 1-ого рода.

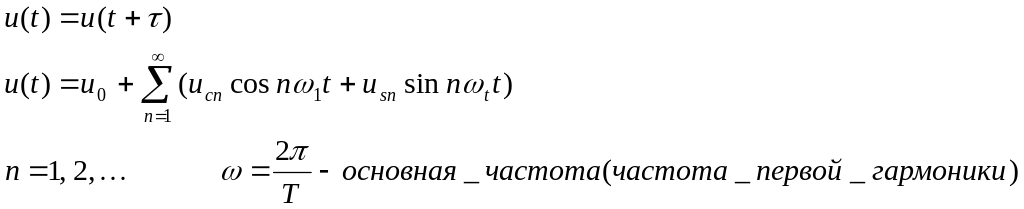
- среднее значение или постоянная составляющая

- амплитуда косинусоидальной составляющей

- амплитуда синусоидальной составляющей

(1)

- амплитуда или максимальное значение гармонической составляющей ряда Фурье

- аргумент или начальная фаза гармонической составляющей ряда Фурье