Топологические матрицы

Узловая матрица A_н =a[i,j], определяется следующим образом: строчками являются узлы схемы, а столбцами соответствующие ветви.

A_н =a_i,j= a_i,j= Матрица состоит из 1, 0, -1

a_i,j=0, если j-ая ветвь не подсоединена к i-ому узлу.

a_i,j= +(-) 1, если j-ая ветвь подсоединена к узлу и направлена от узла (к узлу).

+1

i

-1

Напишем узловую матрицу для своего графа:

A_н= 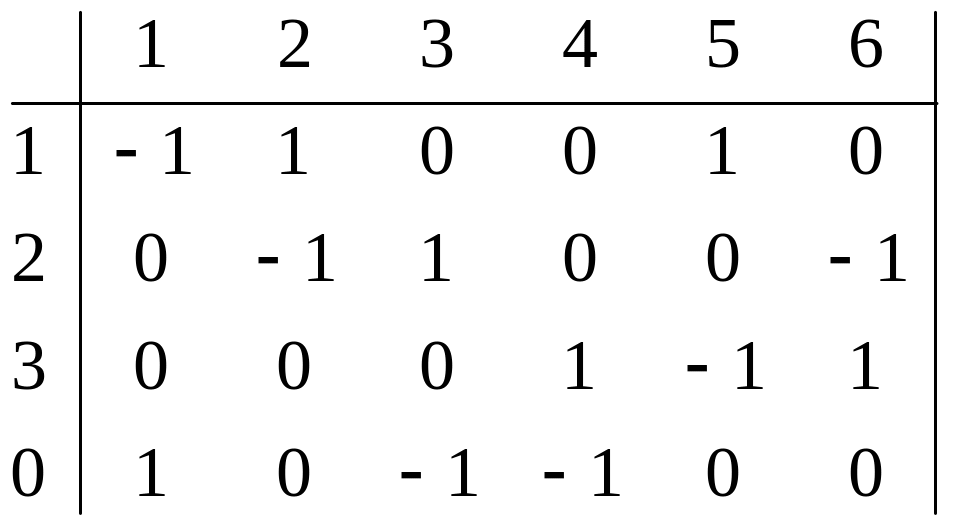=> A_н-> A_i -Неопределенная матрица

Запишем 1-ый з-н Кирхгофа с помощью матрицы:

A_н*i^в =0 i^в= - матрица столбец тока ветвей.

Система алгебраических ур-ний, соответствующая матричному, является системой зависимых ур-ний, т.к. любые ур-ния являются комбинацией других. Для получения линейно независимых ур-ний, один из узлов принимается за базовый, т.е. его потенциал равен нулю, тогда узловая матрица составляется для всех узлов кроме базового

A = 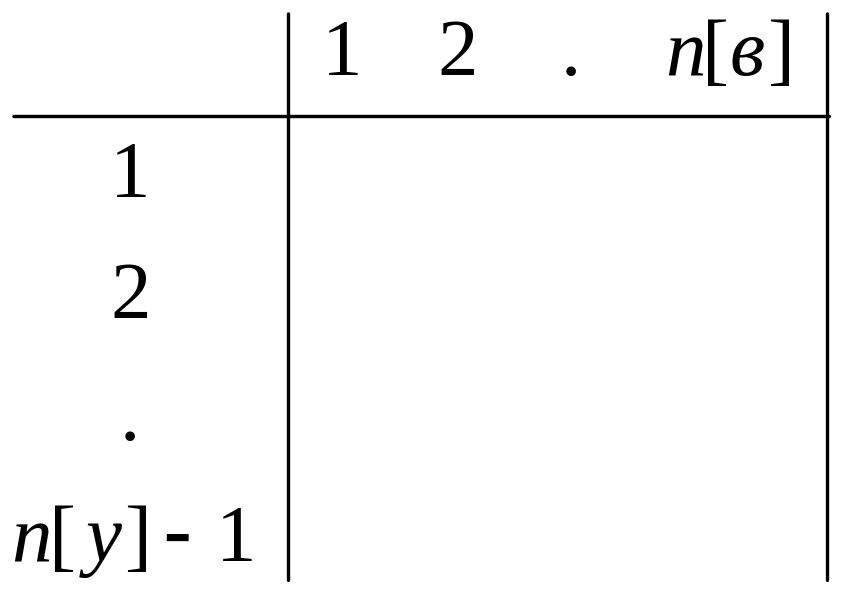=> 1-ый закон Кирхгофа : A_н*i^в =0

Определим напряжение в ветвях с потенциалами узлов, введем матрицы напряжений и потенциалов.

U ^в= - Матрица столбец напряжений в ветвях.

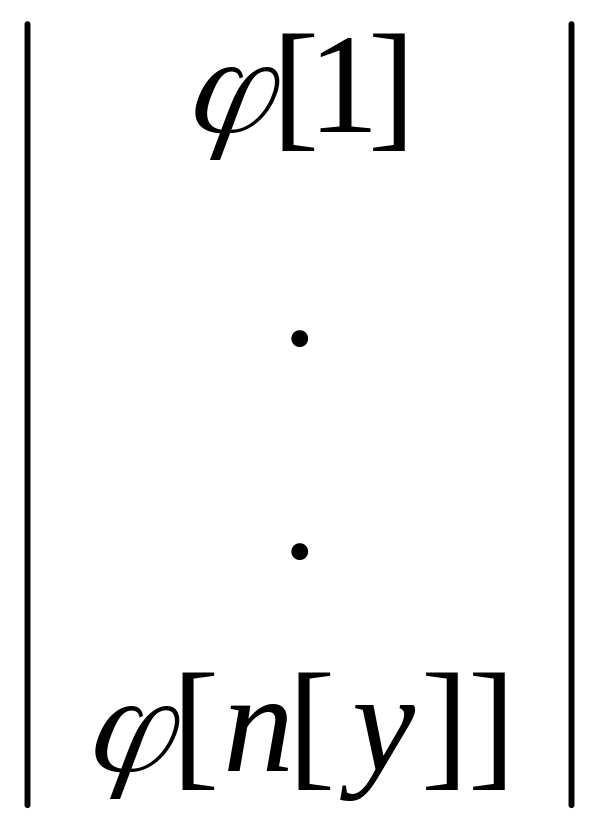= - Матрица столбец потенциалов в узлах.

Запишем следующее узловое преобразование:

U_в = A^T*

Контурная матрица

ветви

В =b_i,j= b[i,j]=

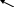Главные контура

b_i,j = 0, если j-ветвь не входит в i-й контур.

b_i,j= +(-), если j-ветвь входит в i-й контур и направление ветви совпадает с направлением контура. Направление контура выбираем по направлению ветви связи (если направлено противоположно)

Дерево - 4-5-6 ветви (см. решение в начале)

Выберем главные контура: I, II, III.

Составим матрицу В

В =

Запишем с помощью матрицы В 2-ой закон Кирхгофа: В* U ^в=0 (система линейно независимых уравнений)

Если В состоит из главного контура, то получим систему независимых уравнений.

.

A*I^в=0 n_I=n^у-1 1-й Закон Кирхгофа

B*U^в=0 n_II=n^в-( n^у-1) 2-й Закон Кирхгофа

U^в=R^в*I^в Закон Ома

Матрицы сопротивлений и проводимости формируются аналогично:

R[в]=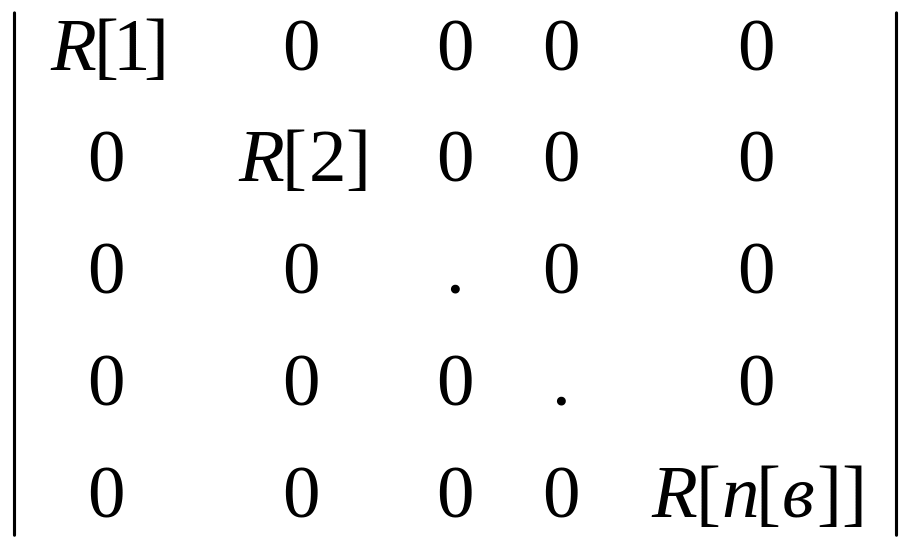

Введем матрицу проводимости ветвей.

G^в=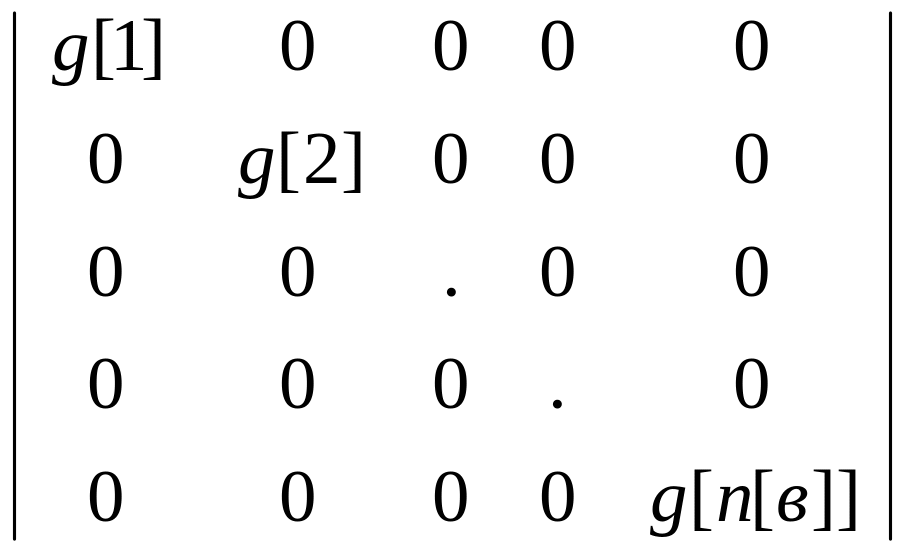

U^в_r=

Закон Ома в матричном виде

U^в_r=R^в*I^в

I^в=G^вU^в_r

Обобщенная ветвь электрической цепи (Закон Ома для обобщенной ветви)

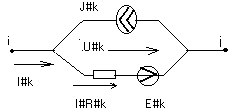U_rk=i*_rk*r_k

U_e=e_k

i j -граф

k

Найдем зависимость напряжения и тока

1-й закон Кирхгофа: I_k=I_{r k} - J_k

I_{r k}=(U_k-E_k)*g_k, g_k=1/(r_k)

I_k=(U_k+E_k)*g_k-J_k - закон Ома для обобщенной ветви

Напишем то же для напряжения:

U_k=(I_k+J_k)*R_k-E_k – обобщенный закон Ома для напряжения обобщенной ветви.

Запишем в матричной форме:

I^в=(U^в + E^в)*G^в - J^в

E^в= J^в=

Уравнение Кирхгофа в матричной форме: A*I^в =0

I^в= I_r^в –J => A*I_r^в=A*J^в - закон Кирхгофа

B*U^в=0 U^в = Ur- E^в

B*U^в= B*E^в - 2-й закон Кирхгофа B* I_r^в *R^в = B*E^в

U_r^в=R^в* I_r^в - закон Ома

Соберем все эти уравнения в одно:

A * I_r^в = A 0 J^в - это уравнение для нахождения тока в ветви

B* R^в 0 B E^в

Перепишем:

I _r^в= A -1 A 0 J^в - это уравнение для нахождения тока в ветвях

B* R^в 0 B E^в

_____ ______

\ /

H

n_в - число строк

2n_в - число столбцов H=n_в*2n_в

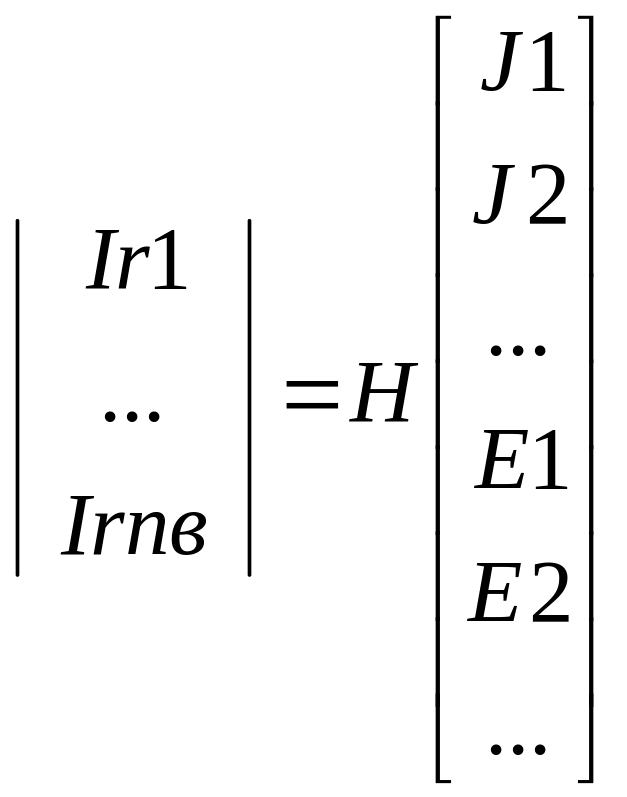
I_rj=kⁱ_j1*J₁+kⁱ_j2*J₁+…+g_j1*E₁+g_j2*E₂+…+g_jj*E_j+…

U_rj=r_j*I_rj=r_j1*J₁+r_j2*J₂+…+k_j1*E₁+…+k_jj*E_j+…