Добротность r-l-c контура

₀*L)/r = = =Q-добротность

1/(₀*C*r) = = =Q

Q=(₀*L)/r=1/(₀*C*r)

z_вх(j)=r+j(L-1/(C))=r+j₀L(/₀-₀/)=r*[1+j*(₀*L)*v/r]=r[1+jQv]

Предаточная функция последовательной r-l-c цепи

а) Каноническая форма записи предаточной ф-ции схемы 2-го порядка

H(p)=(b₂*p²+b₁*p+b₀)/(p²+(₀/Q)*p+^₀) p=j

1) H(j)= _вых/ _вх=( *r)/( *z_вх(j))

H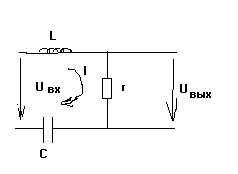 (p)=r/z_вх(p)=r/(r+pL+1/(p*C))=rpc/(p²*L*C+prc+1)=

=(rp/L)/(p²+(r/L)*p+1/(LC))=(p₀/Q)/(p²+(₀/Q)*p+^₀)

z_L=jL=pL

z_C=1/(jC)=1/(pC)

r/l=₀r/(₀L)=₀/q

H(j)=(j*(₀/q))/((²₀-²)+j₀/Q)

|H(j)|=H()=(₀/Q)/ φ()=π/2-arctg((*₀)/(Q*(^₀-²)))

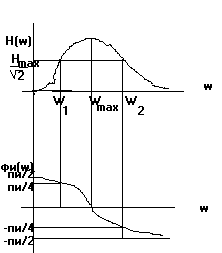
АЧХ

ФЧХ

Это ППФ

d=₂-₁- полоса пропускания

Q=₀/d - чем уже d,тем выше Q

= =

2 )H(p)= _вых/ _вх= *z_c/ *z_вх=(1/(p*c))/(r²+pL+1/(pc))=1/(p²Lc+pcr+1)=(1/(Lc))/(p²+p*r/L+1/(Lc))=₀/(p²+₀*p/Q+₀)

АЧХ

|H(j)|=²₀/((²₀-²)+(₀/Q)j)

ФЧХ

φ ()=0-arctg(₀/(Q*(²₀-²)))

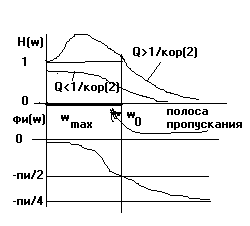 _max=₀

1/(2*Q²)<1 --> Q>

3)H(p)= _вых/ _вх=( *z_L)/( *z_вх)=(Lp)/(r+pL+1/(pc))= p²*Lc/(p²Lc+prc+1)=p²/(p²+p₀/Q+^₀)

| H(j)|=H()=-²/

H(j)=-²/((^₀-²)+(₀/Q)*jw)

φ (w)= π -arctg(₀/(Q*(^₀-²)))

_max=₀/

4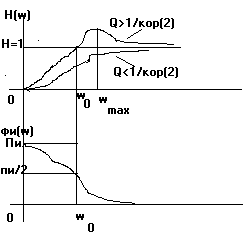 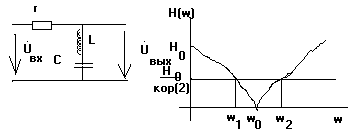) Полосно заграждающий фильтр ₂-₁ – полоса загрождения

НЧ

H(p)=H₀*^₀/(p²+₀*p/Q+^₀)

ВЧ

H(p)=H₀*p²/(p²+₀*p/Q+^₀)

ПП

H(p)=H_max*p/(p²+₀*p/Q+^₀)

ПЗ

H(p)=H₀*(p²+^₁)/ (p²+₀*p/Q+^₀)

Коммутация

Определение. Коммутация (изменение параметров) может быть в результате подключения или отключения источников или в результате подключения и отключения элементов цепи.

Идеальный ключ (_/ _)

R_кз=0 R_р=0

Время за которое ключ включается (t комутации)

t=_0=0_ - t непосредственно перед комутацией

t=₊0=₊0 - t непосредственно после комутации

t_к=t ₀₊-t₀

V₁(t) R L C Y₁(t)

U итд V₁(t)

V₂(t) Y₂(t) V(t) = V₂(t)

. X₁(t), … ,X_n(t) . .

. X(t) . V_n(t)

V_n(t) Y_n(t)

V(t) – матрица-столбец внешних переменных (независимые источники Y и U).

Y(t) - матрица столбец искомых выходных переменных .

Y₁(t) X₁(t)

Y(t)= Y₂(t) X(t)= X₂(t)

. .

Y_n(t) X_n(t)

X(t) – матрица внутренних переменных (переменные состояния).

Замечание: в качестве переменных состовляющих рассматриваются токи в L элементах и U на C элементах, т.к. эти элементы полностью определяют электронное состояние цепи в любой момент t.

W_М=L*(i_L)²/2 W_Э =C*(U_c)²/2

Для анализа цепи рассматриваются компонентные и топологические уравнения.

Компонентные уравнения Топологические

Ur(t)=r_i(t) I A*i(t)=0

U_L(t)=L*(di_L/dt) II B*i(t)=0

i_C(t)=C*(dU_C/dt)

Эти уравнения справедливы для всех ком. t.

Для произвольной линейной цепи в результате преобразования уравнений Киргофа и компонентных уравнений можно получить систему n диф. уравнений 1-ого порядка.

Эти n уравнения составленные для переменных состояния (X(t)) называются матричными уравнениями состояния.

1. dX(t)/dt=X’(t)=A₁*X(t)+B₁*V(t)

2. Y(t)=A₂*X(t)+B₂*V(t)

A₁=[n x n] A₂=[m x n] B₁=[n x n] B₂=[n x m]

Преобразуем эту систему уравнений в дифферанциальные уравнения n-ого порядка.

a_n*(dⁿx/dtⁿ) + a_n-1*(d^n-1x/dt^n-1)+…+a₁*(dx/dt) + a₀*x=0

для нахождения общего решения однородного уравнения составим характеристическое уравнение. dx/dt & (&-это лямбда)

a_n*&ⁿ + a_n-1*&^n-1+…+a₁*& + a₀=0 Получилось n корней.

X_OO= E_(k=1-n)A_K*e^&k*t E_(k=1-n) - означает сумма по k от 1 до n, &k-&_k