17.Проекция вектора.Разложение вектора по системе вектора. Координаты вектора.

 Проекции вектора

Здесь и в дальнейшем под словами "проекция точки" или "проекция вектора" всегда будем понимать ортогональную проекцию.

Пусть в пространстве задана некоторая ось , то есть прямая, на которой отмечена фиксированная точка и заданы направление и единица длины. Тогда каждой точке оси соответствует некоторое число.

        Определение 10.21   Проекцией точки на ось называется число, соответствующее основанию перпендикуляра , опущенного на ось из точки .         

        Определение 10.22   Проекцией вектора на ось называется разность проекций конца вектора и его начала.         

Проекцию будем обозначать . На рис. 10.18 .

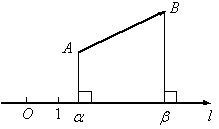
Рис.10.18.Проекция вектора на ось

Легко проверить, что если , то , то есть проекция не зависит от положения начала вектора, а зависит только от самого вектора.

Разложение вектора по базису

        Определение 10.10   Множество векторов на прямой назовем одномерным векторным пространством, множество векторов на плоскости -- двумерным векторным пространством, в пространстве -- трехмерным векторным пространством.         

Легко проверить, что если  -- какое-то векторное пространство, ,  -- число, то и .

        Определение 10.11   Линейной комбинацией векторов с коэффициентами называется вектор .         

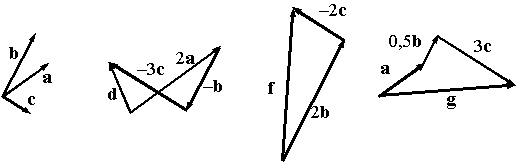
Рис.10.10.Примеры линейных комбинаций

Векторы d,f,g на рисунке 10.10 и являются линейными комбинациями векторов a,b,c: , , , .

Будем говорить, что вектор b раскладывается по векторам , если b является линейной комбинацией этих векторов.

Координаты вектора

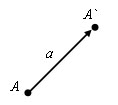Есть вектора a. Пусть A (x; y) – начло вектора, а A` (x`; y`) – конец вектора. Координатами вектора a называются числа a1=x-x`, a2=y-y`. Для обозначения того, что вектор a имеет координаты a1 и a2, используют запись a (a1; a2) или (a1; a2). Абсолютная величина вектора a (a1; a2) равна Если начало вектора совпадает с его концом, то это нулевой вектор , обозначается (0).

18. Декартовы координаты точки, вектора. Деление отрезка в заданном отношении.

Ключевые слова: вектор, координаты, длина вектора

Прямые x, y, z называются координатными осями (или осями координат), точка их пересечения O – началом координат, а плоскости xOy, xOz и yOz – координатными плоскостями. Точка O разбивает каждую координатную ось на две полупрямые, которые называются положительной и отрицательной полуосями.

Координатой точки A по оси x будем называть число, равное по абсолютной величине длине отрезка OA_x: положительное, если точка A лежит на положительной полуоси x, и отрицательное, если она лежит на отрицательной полуоси.

Аналогично можно определить координаты y и z точки A. Координаты точки A записываются в скобках рядом с названием этой точки: A (x; y; z).

Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси.

• Единичный вектор, направленный вдоль оси x, обозначается i .

• Единичный вектор, направленный вдоль оси y, обозначается j .

• Единичный вектор, направленный вдоль оси z, обозначается k .

Вектора i , j , k называются координатными векторами.

• Любой вектор a можно разложить по координатным векторам: a =x i +y j +z k.

• Коэффициенты разложения определяются единственным образом и называются координатами вектора a в данной системе координат.