13.Метод Гаусса исследования и решения систем линейных уравнений.

Ме́тод Га́усса[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные[2].

Пусть исходная система выглядит следующим образом

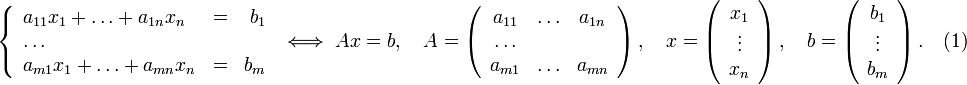
Матрица A называется основной матрицей системы, b — столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

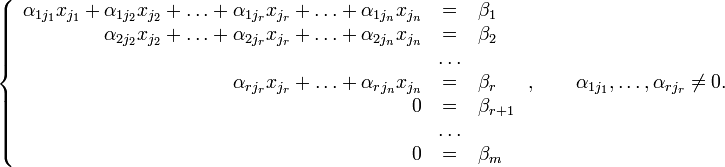
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных [3].

Тогда переменные называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число , где i > r, то рассматриваемая система несовместна.

Пусть для любых i > r.

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом ( , где — номер строки):

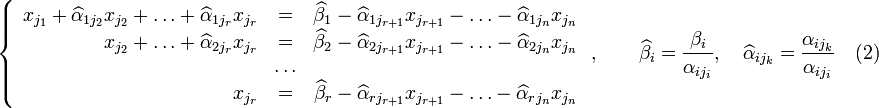, где

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

14.Системы однородных линейных уравнений. Условие единственности решения.

Однородные системы линейных уравнений

Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.

Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

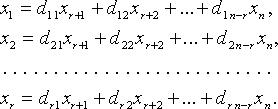
Тогда n - r линейно независимыми вектор-решениями будут:

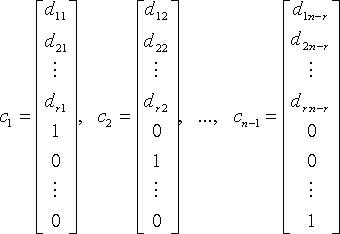
а любое другое решение является их линейной комбинацией. Вектор-решения образуют нормированную фундаментальную систему.

В линейном пространстве множество решений однородной системы линейных уравнений образует подпространство размерности n - r; - базис этого подпространства.