33

1. Электрический заряд.

Свойства электрического заряда. Единица электрического заряда Кулон (Кл). а)Заряд существует в двух видах. Тела, заряженные одноименным знаком отталкиваются, а разноименным притягиваются. б)Электрический заряд инвариантен. Его величина не зависит от системы отсчета, т.е. не зависит от того движется он или покоится. в)Электрический заряд дискретен. Заряд не может уменьшаться до бесконечно малого значения. г)Электрический заряд аддитивен. Заряд системы тел равен сумме зарядов тел входящих в систему. д)подчиняется Закону сохранения электрического заряда: что алгебраическая сумма зарядов любой замкнутой системы остаётся неизменной какие бы процессы не происходили внутри данной системы.

Зако́н Куло́на- Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме направлена вдоль прямой, соединяющей заряды, прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними. Закон Кулона в вакууме: .Электрическая постоянная: ε₀=8,85·10^-12 Кл²/Н·м² или Ф/М. В изотропной среде . ε=F₀/F – диэлектическая постоянная (проницаемость) среды

Напряжённость эп— векторная физическая величина, опред-я силой действующей на единичный положительный заряд, помещённый в данную точку поля: [Н/Кл, В/М]

Связь между напряженностью и потенциалом электростатического поля: Заряд. Закон Кулона.

1) Сила взаимодействия между двумя точечными зарядами: [Н]

ε_воздуш = 1, q [Кл] - заряд, r [м] – расстояние между зарядами.

2) Напряженность поля точечного заряда: , где r – расстояние от заряда до точки, в которой ищем заряд этого поля.

Расчет напряженности эл. поля с помощью теоремы О-Г.

1) Напряженность поля бесконечно заряженной плоскости: где σ – поверхностная плотность заряда на плоскости: [Кл/м²].

2) Напряженность поля двух заряженных плоскостей (поле плоского конденсатора):

3) Напряженность поля сферы (шара): , (r ≥ R)

r – расстояние от центра сферы до точки напряженности. Если r < R, то E = 0.

4) Напряженность поля заряженной нити: , где τ – линейная плотность заряда на нити: [Кл/м].

2. Работа электростатического поля.

Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда из одной q_пр точки электростатического поля в другую на отрезке пути dl , по определению равна

где α - угол между вектором силы F и направлением движения dl. Если работа совершается внешними силами, то dA₀. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении пробного заряда q из точки “а” в точку “b” будет равна

где   - кулоновская сила, действующая на пробный заряд q_пр в каждой точке поля с напряженностью Е. Тогда работа

Пусть заряд q перемещается в поле заряда q из точки “а”, удалённой от q_пр на расстоянии r₁ в точку “b”, удаленную от q_пр на расстоянии r₂ (рис 1.12).

Как видно из рисунка   тогда получим

Как было сказано выше, работа сил электростатического поля, совершаемая против внешних сил, равна по величине и противоположна по знаку работе внешних сил, следовательно

Потенциальная энергия заряда в электрическом поле. Работу, совершаемую силами электрического поля при перемещении положительного точечного заряда q из положения 1 в положение 2, представим как изменение потенциальной энергии этого заряда:  ,

где W_п1 и W_п2 – потенциальные энергии заряда q в положениях 1 и 2. При малом перемещении заряда q в поле, создаваемом положительным точечным зарядом Q, изменение потенциальной энергии равно

 .

При конечном перемещении заряда q из положения 1 в положение 2, находящиеся на расстояниях r₁ и r₂ от заряда Q,

 .

Если поле создано системой точечных зарядов Q₁, Q₂,¼, Q_n, то изменение потенциальной энергии заряда q в этом поле:

 .

Приведённые формулы позволяют найти только изменение потенциальной энергии точечного заряда q, а не саму потенциальную энергию. Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q, находящегося в электрическом поле, созданном другим точечным зарядом Q, получим

 ,

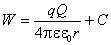где C – произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q (при r ® ¥), тогда постоянная C = 0 и предыдущее выражение принимает вид

 .

При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную. В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q:

 .

Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Q_i (i = 1, 2, ... ,n). Энергия взаимодействия всех n зарядов определится соотношением

 ,

где r_ij - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.

Потенциал электростатического поля. Поле консервативной силы может быть описано не только векторной функцией, но эквивалентное описание этого поля можно получить, определив в каждой его точке подходящую скалярную величину. Для электростатического поля такой величиной является потенциал электростатического поля, определяемый как отношение потенциальной энергии пробного заряда q к величине этого заряда, j = W_п / q, откуда следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Единицей измерения потенциала служит Вольт (1 В).

Потенциал поля точечного заряда Q в однородной изотропной среде с диэлектрической проницаемостью e :

 .

Принцип суперпозиции. Потенциал есть скалярная функция, для неё справедлив принцип суперпозиции. Так для потенциала поля системы точечных зарядов Q_1, Q₂¼, Q_n имеем

 ,

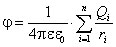где r_i - расстояние от точки поля, обладающей потенциалом j, до заряда Q_i. Если заряд произвольным образом распределен в пространстве, то

 ,

где r - расстояние от элементарного объема dx, dy, dz до точки (x, y, z), где определяется потенциал; V - объем пространства, в котором распределен заряд.

Потенциал и работа сил электрического поля. Основываясь на определении потенциала, можно показать, что работа сил электрического поля при перемещении точечного заряда q из одной точки поля в другую равна произведению величины этого заряда на разность потенциалов в начальной и конечной точках пути, A = q (j₁ - j₂). Если по аналогии с потенциальной энергией считать, что в точках, бесконечно удалённых от электрических зарядов - источников поля, потенциал равен нулю, то работу сил электрического поля при перемещении заряда q из точки 1 в бесконечность можно представить как A_¥ = q j₁. Таким образом, потенциал â данной точке электростатического поля - этофизическая величина, численно равная работе, совершаемой силами электрического поля при перемещении единичного положительного точечного заряда из данной точки поля в бесконечно удаленную: j = A_¥ / q. В некоторых случаях потенциал электрического поля нагляднее определяется какфизическая величина, численно равная работе внешних сил против сил электрического поля при перемещении единичного положительного точечного заряда из бесконечности в данную точку. Последнее определение удобно записать следующим образом:

 .

В современной науке и технике, особенно при описании явлений, происходящих в микромире, часто используется единица работы и энергии, называемая электрон-вольтом (эВ). Это работа, совершаемая при перемещении заряда, равного заряду электрона, между двумя точками с разностью потенциалов 1 В: 1 эВ = 1,60×10^-19 Кл×1 В = 1,60×10^-19 Дж.