Вопрос 24. Корреляция
Корреля́ция (корреляционная
зависимость)
— статистическая взаимосвязь
двух или нескольких случайных
величин (либо
величин, которые можно с некоторой
допустимой степенью точности считать
таковыми). При этом изменения значений
одной или нескольких из этих величин
сопутствуют систематическому изменению
значений другой или других величин.
Математической мерой корреляции двух
случайных величин служит корреляционное
отношение 
,
либо коэффициент
корреляции 
(или 
).
В случае, если изменение одной случайной
величины не ведёт к закономерному
изменению другой случайной величины,
но приводит к изменению другой
статистической характеристики данной
случайной величины, то подобная связь
не считается корреляционной, хотя и
является статистической.
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.
Свойства коэффициента корреляции
Неравенство Коши — Буняковского:
если
принять в качестве скалярного
произведения двух
случайных величин ковариацию 
,
то норма случайной величины будет
равна 
,
и следствием неравенства
Коши — Буняковского будет:
.
Коэффициент корреляции равен
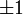тогда
и только тогда, когда X и Y линейно
зависимы (исключая события нулевой
вероятности, когда несколько точек
«выбиваются» из прямой, отражающей
линейную зависимость случайных величин):
,
где 
.
Более того в этом случае знаки 
и k совпадают:
.
------------------------------------------------------------------------------------------------------------------------------------------------------------
Вопрос 25. Использование пакета анализа Excel для вычисления статистических показателей.
То, что выделено синим цветом, скорее всего будет вами не использовано, но на всякий случай это оставил)
Методические рекомендации.
Обращение к каждой функции состоит из двух частей: имени функции и аргументов в круглых скобках. Аргументы функции могут быть следующих типов:
1)числовые константы, например, функция ПРОИЗВЕД(2;3) вычисляет произведение чисел 2 и 3, т.е. 2·3.
2)ссылки на ячейки и блоки ячеек (функция ПРОИЗВЕД (А1;С1:СЗ) вычисляет произведение содержимого ячеек А1,С1,С2 и С3, т.е. А1·С1·С2·СЗ
3) текстовые константы (заключенные в кавычки).
4) логические значения.
5) массивы.
6) имена ссылок, например, если ячейке А10 присвоить имя СУММА (последовательность команд Вставка, Имя, Определить.. .),а блоку ячеек В10:Е10 -имя ИТОГИ , то допустима следующая запись: =СУММ(СУММА; ИТОГИ).
7) смешанные аргументы, например, =СРЗНАЧ (Группа;АЗ;5*3)
Формулы, содержащие функции, можно вводить непосредственно в ячейку, в строку формул или создавать с помощью Мастера функций. Для вызоваМастера функций необходимо выбрать команду Функция в меню Вставка или нажать кнопку Мастер функций (значок fx ). B открывшемся диалоговом окне выберите категорию и имя функции, затем в поля с соответствующими подсказками введите аргументы. После нажатия кнопки Закончить готовая функция появится в строке формул
Пример 1. Вычислить значение функции у = ех · sin(x) для -1=< х <=1 c с шагом ?х=0,2 . Определить количество отрицательных у.
Заполним столбец А значениями аргумента функции. Чтобы не вводить их вручную , применим следующий прием. Введите в ячейку А1 начальное значения аргумента -1 . В меню Правка выберите команду Заполнить, затем Прогрессия и в открывшемся диалоговом окне укажите предельное значение
(1),шаг(0.2 ) и направление (По столбцам). После нажатия кнопки ОК в столбце А будут введены все значения аргумента . В ячейку В1 введите формулу : =exp(А1)* sin(AI). Размножьте эту формулу на остальные ячейки столбца В, ухватив левой мышью черный квадратик в правом нижнем углу рамки выделенной ячейки В1 и протащив рамку до конца изменения аргумента . В итоге будут вычислены соответствующие значения функции.
Для определения количества отрицательных у в ячейку С1 введите формулу =СЧЕТЕСЛИ (В 1: В 11; <0). В результате в ячейке С1 будет вычислено количество отрицательных значений в ячейках В1:В11 (т.е. у ). Принцип действия большинства логических функций Excel заключается в проверке некоторого условия и выполнения в зависимости от него тех или иных действий. Так, функция ЕСЛИ выполняет проверку условия, задаваемого первым аргументом логического выражения: ЕСЛИ (логичическое 1; значение_да; значение нет) и возвращает значение да, если условие выполнено(ИСТИНА) , и значение нет, в противном случае (ЛОЖЬ).
Дополнительные логические функции:
=И (логическое выражение 1; логическое выражение 2;...) – возвращает значение ИСТИНА, если все аргументы истинны, и ЛОЖЬ, если хотя бы один аргумент – ЛОЖЬ.
Например, для =ЕСЛИ(СУММ(А1:А10)>0; И; СУММ(В1:В10)>0; СУММ(А1:В10);0). Если суммы и в столбце А1:А10 и в столбце В1: В10 положительны , то вычислить сумму значений в ячейках А1:В10 , иначе - 0.
Аналогично используются:
=ИЛИ (логическое 1;логическое 2;...) – возвращает значение ИСТИНА, если хотя бы один аргумент является - ИСТИНА
=НЕ (флаг) – меняет значение ИСТИНА на ЛОЖЬ и наоборот.