Занятие № 8 Тема: Элементы теории вероятностей

Вопросы

1. Вероятность и функция распределения. Условие нормировки.

2. Распределения Гаусса и Пуассона.

3. Вычисление средних и средних квадратичных значений физических величин.

Задачи

8.1 Доказать, что для двух независимых величин L и M имеют место равенства: , .

8.2 Доказать, что , где .

8.3 Найти , и при равномерном распределении величины L между a и b.

8.4 Найти , и для нормированного экспоненциального распределения , где .

8.5 Найти , и для нормированного гауссовского распределения 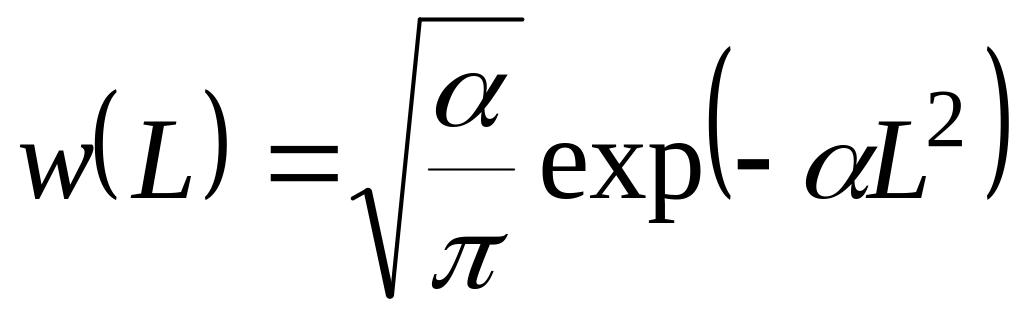, где .

8.6 Найти функцию распределения по углам для точки, равномерно движущейся по окружности.

8.7 Математический маятник совершает гармонические колебания по закону  = ₀cos(2 t/T), где . Найти вероятность того, что при случайном измерении угла отклонения  маятника полученное значение будет лежать в интервале от  до  + d.

8.8 Дискретная случайная величина n может принимать целые положительные значения от 0 до  и подчиняется распределению Пуассона 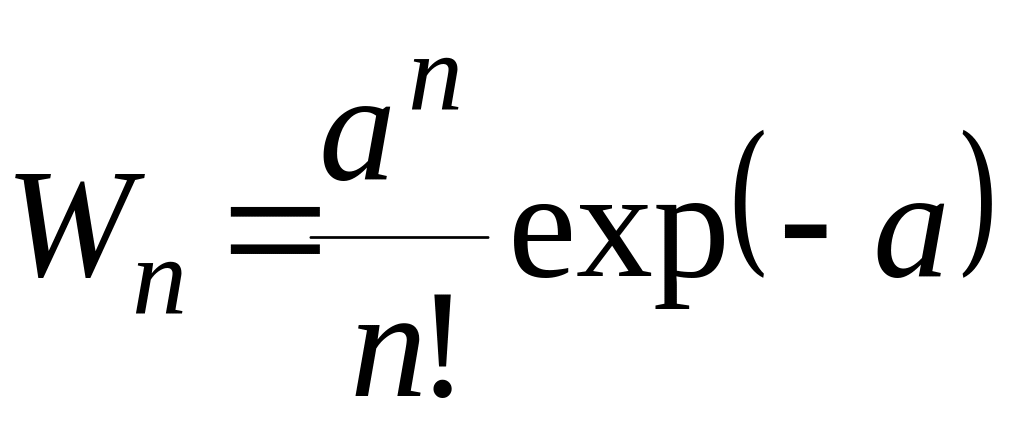, где a = const. Показать, что распределение Пуассона подчиняется условию нормировки на 1, и найти среднее значение случайной величины n.

8.9 Вероятность того, что для некоторой системы значения величин x и y одновременно лежат в интервалах [x, x + dx], [y, y + dy] равна , где  > 0, , . Найти константу С и вероятность того, что значение величины x будет лежать в интервале [x, x + dx].

8.10 Идеальный газ из N молекул находится в сосуде объемом V. Определить вероятность того, что в заданном объеме V₀ < V будет содержаться в данный момент n молекул. Рассмотреть предельные случаи: 1) n << N; 2) n >> 1, .

Занятие № 9 Тема: Каноническое распределение Гиббса

Вопросы

1. Микроканоническое и каноническое распределения Гиббса.

2. Термодинамический смысл параметров канонического распределения.

3. Статистический смысл энтропии.

Задачи

9.1 Используя каноническое распределение Гиббса, доказать, что .

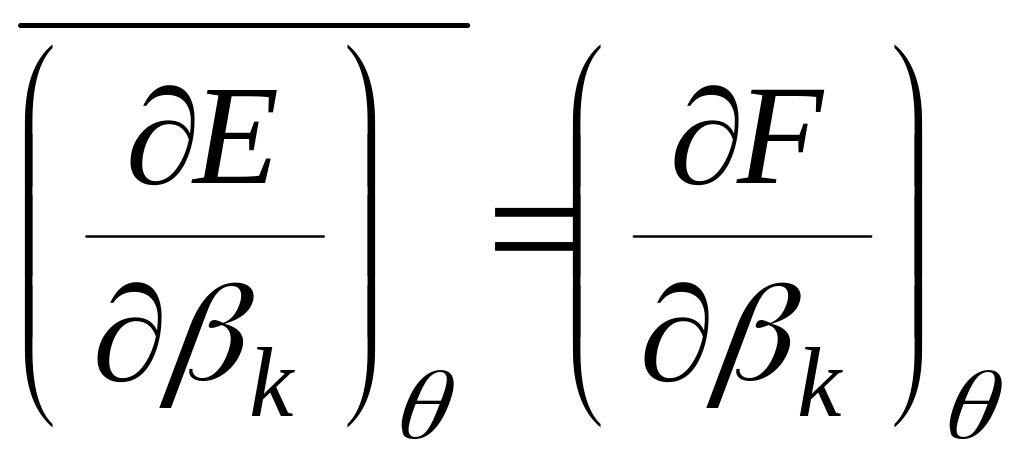9.2 Используя каноническое распределение Гиббса, показать, что для произвольной физической величины f (p, q) имеет место соотношение 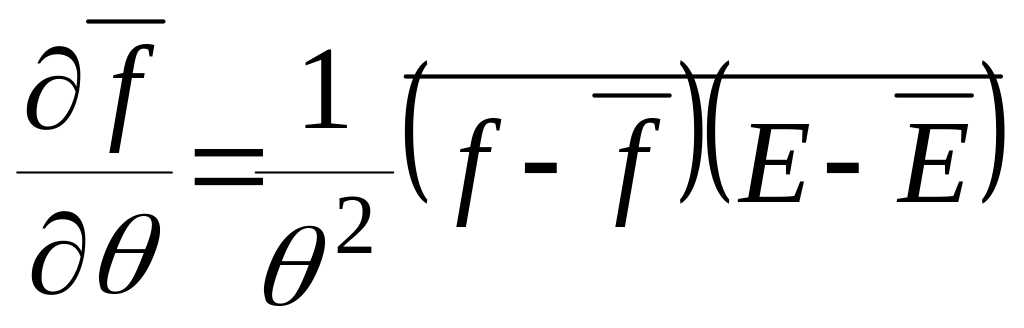(усреднение проводится по фазовому ансамблю).

9.3 Доказать, что для произвольной физической величины f (p, q, ) имеет место соотношение .

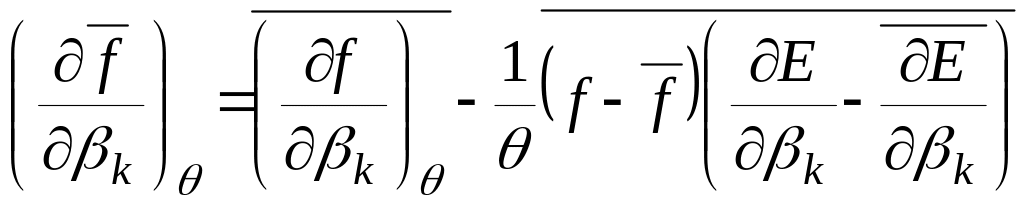9.4 Доказать, что для произвольной физической величины f (p, q) справедливы равенства: ; .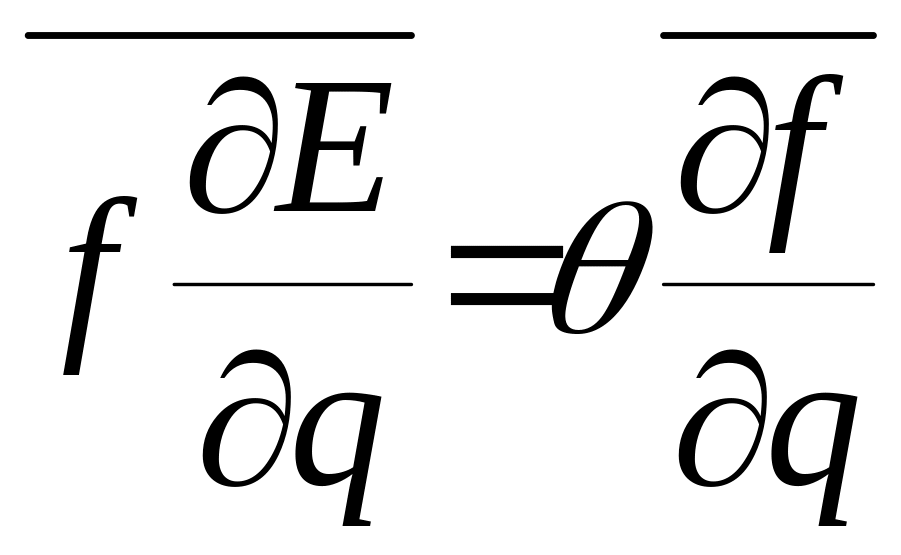

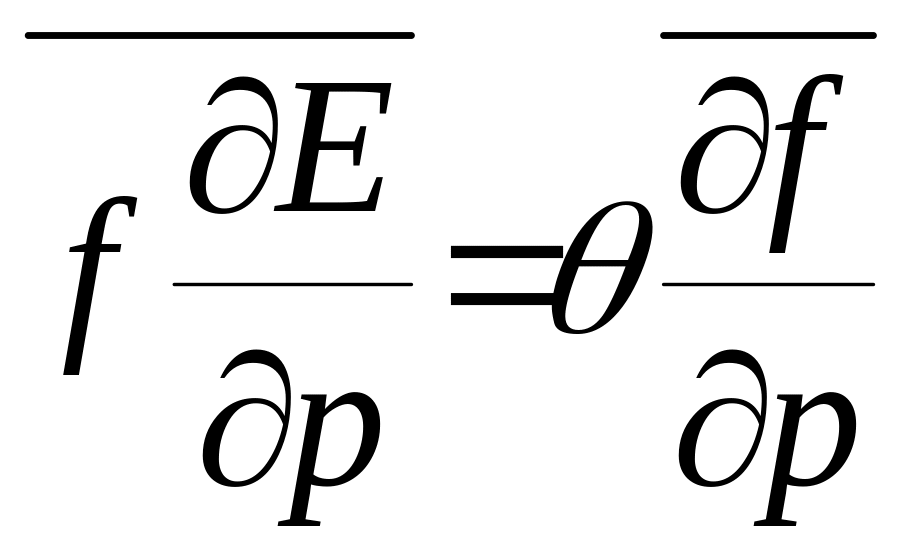9.5 Доказать, что для любой квазизамкнутой системы имеет место соотношение .

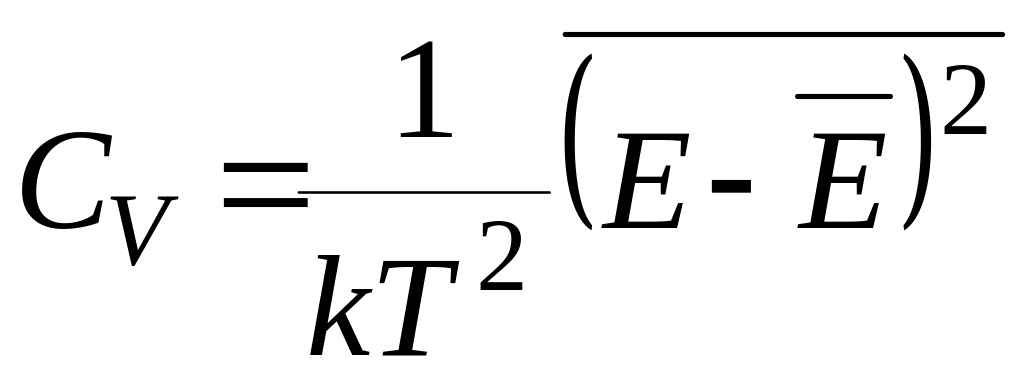9.6 Показать, что для систем с очень большим числом частиц каноническое распределение Гиббса переходит в микроканоническое распределение.

9.7 Показать, что интеграл состояний системы можно представить в виде произведения интегралов состояний ее независимых частей.

9.8 Найти выражения для термодинамического потенциала Гиббса, энтальпии и энтропии через интеграл состояний.

9.9 Записать в классическом приближении распределение Гиббса по энергиям для линейного гармонического осциллятора и вычислить среднее значение его энергии.

9.10 В системах, содержащих большое число N частиц, средние энергии связаны с температурой соотношениями: а) E = NkT; б) E = aT ⁿ (n >> 1). Найти соответствующее данной энергии число состояний каждой системы.