
- •1. Гармонические колебания (способы представления, характеристика величин).
- •7. Сложение колебаний, направленных по одной прямой (постановка задачи и анализ результата).
- •8. Сложение взаимно-перпендикулярных колебаний (постановка задачи и анализ результата).
- •9. Уравнение бегущей волны (формулы, графики, физический смысл величин, входящих в него).
1. Гармонические колебания (способы представления, характеристика величин).
В
технике и окружающем нас мире часто
приходится сталкиваться
спериодическими (или почти
периодическими)
процессами, которые повторяются через
одинаковые промежутки времени. Такие
процессы называют колебательными.
Гармонические
колебания
описываются уравнением x = xm cos (ωt + φ0),
где х- смещение тела от положения
равновесия, xm – амплитуда колебаний,
то есть максимальное смещение от
положения равновесия, ω –циклическая
или круговая частота колебаний,
t – время. Величина, стоящая под знаком
косинуса φ = ωt + φ0
называется фазой гармонического
процесса. При t = 0 φ = φ0,
поэтому φ0 называют начальной
фазой. Минимальный
интервал времени, через который
происходит повторение движения тела,
называется периодом
колебаний T.
Физическая величина, обратная периоду
колебаний, называется частотой
колебаний:
![]() Частота
колебаний f показывает, сколько колебаний
совершается за 1 с. Единица частоты
– герц
(Гц).
Частота колебаний f связана с циклической
частотой ω и периодом колебаний T
соотношениями:
Частота
колебаний f показывает, сколько колебаний
совершается за 1 с. Единица частоты
– герц
(Гц).
Частота колебаний f связана с циклической
частотой ω и периодом колебаний T
соотношениями:
![]()
2. Напишите дифференциальное уравнение свободных колебаний и объясните его решение. |
Дифференциальное
уравнение свободных колебаний заряда
в контуре(при R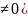 имеет
вид:
имеет
вид:
 =0
Учитывая выражение
=0
Учитывая выражение
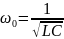 (1) и принимая коэффициент затухания
(1) и принимая коэффициент затухания
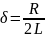 дифференциальное уравнение можно
записать в идентичном уравнению
дифференциальное уравнение можно
записать в идентичном уравнению
![]() (2) виде:
(2) виде:
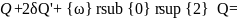 Из
выражений (2) и s
Из
выражений (2) и s![]() вытекает, что колебания заряда совершаются
по закону
вытекает, что колебания заряда совершаются
по закону
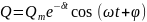 с частотой, согласно
с частотой, согласно
 ,
,
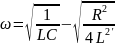 (3) меньшей собственной частоты контура
(3) меньшей собственной частоты контура
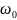 .
При R=0
формула (3) переходит в (1).
.
При R=0
формула (3) переходит в (1).
|
3. Напишите дифференциальное уравнение затухающих колебаний и объясните его решение.
,где
δ = const=
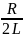 — коэффициент
затухания.
Решение этого уравнения ищем в виде
s(t)=f(t)exp(-δt),
тогда после подстановки получим:
— коэффициент
затухания.
Решение этого уравнения ищем в виде
s(t)=f(t)exp(-δt),
тогда после подстановки получим:
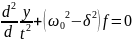 .
Тогда
.
Тогда
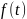 -
гармоническая функция, т.е.
-
гармоническая функция, т.е.
 (но уже с другой частотой
(но уже с другой частотой
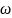 ,
где
,
где
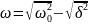 )
и следовательно s(t)=
)
и следовательно s(t)= .
Т.е. при условии
.
Т.е. при условии
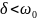 мы можем описать эту зависимость как
гармонические колебания, у которых
амплитуда экспоненциально убывает со
временем. Такие колебания называются
затухающими. Энергия этих колебаний
убывает со временем . зная зависимость
заряда на конденсаторе от времени, мы
можем написать и зависимость тока на
катушке от времени, поскольку I(t)=
мы можем описать эту зависимость как
гармонические колебания, у которых
амплитуда экспоненциально убывает со
временем. Такие колебания называются
затухающими. Энергия этих колебаний
убывает со временем . зная зависимость
заряда на конденсаторе от времени, мы
можем написать и зависимость тока на
катушке от времени, поскольку I(t)=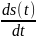 .
Также можно найти зависимость напряжения
на сопротивлении от времени: U=I*R.
Графики всех этих величин выглядят
примерно одинаково, отличаясь начальной
фазой и амплитудой. Если же
.
Также можно найти зависимость напряжения
на сопротивлении от времени: U=I*R.
Графики всех этих величин выглядят
примерно одинаково, отличаясь начальной
фазой и амплитудой. Если же
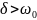 то колебания затухают за время меньше
одного периода колебаний. Такое решение
называется апериодическим и колебаний
в контуре не будет. Для возникновения
в контуре необходимо, чтобы выполнялось
условие
то колебания затухают за время меньше
одного периода колебаний. Такое решение
называется апериодическим и колебаний
в контуре не будет. Для возникновения
в контуре необходимо, чтобы выполнялось
условие

4. Напишите дифференциальное уравнение вынужденных колебаний и объясните его решение.
Чтобы
в реальной колебательной системе
осуществлять незатухающие колебания,
надо компенсировать каким-либо потери
энергии. Такая компенсация возможна,
если использовать какой-либо
периодически действующего фактора
X(t), который изменяется по гармоническому
закону:
Где
|
|
5. Резонанс. Резона́нс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.
Резонансная
частота равна:
|
|
6. Выведите формулу периода колебаний для математического маятника.
Математический
маятник- это идеализированная система,
состоящая из материальной точки
массой m,
подвешенной на нерастяжимой невесомой
нити, и колеблющаяся под действием
силы тяжести. Хорошим приближением
математического маятника является
небольшой тяжелый шарик, подвешенный
на тонкой длинной нити. Момент инерции
математического маятника:
|
|
|
|

 =
=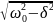
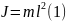 ,
где
,
где
 -
длина маятника. Т.к. математический
маятник можно представить как частный
случай физического маятника,
предположив, что вся его масса
сосредоточена в одной точке- центре
масс, то, подставив выражение (1) в
формулу
-
длина маятника. Т.к. математический
маятник можно представить как частный
случай физического маятника,
предположив, что вся его масса
сосредоточена в одной точке- центре
масс, то, подставив выражение (1) в
формулу
 , где
, где
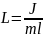 -приведенная длина физического
маятника(Физ. Маятник- твердое тело,
совершающее под действием силы
тяжести колебания вокруг неподвижной
горизонтальной оси, проходящей через
точку О, не совпад. С центром масс С
тела), видим, что если приведенная
длина L
физического маятника равна длине
математического маятника, то периоды
колебаний этих маятников одинаковы.
Следовательно, приведенная длина
физ. Маятника- длина такого
математического маятника, период
колебаний которого совпадает с
периодом колебаний данного физического
маятника.
-приведенная длина физического
маятника(Физ. Маятник- твердое тело,
совершающее под действием силы
тяжести колебания вокруг неподвижной
горизонтальной оси, проходящей через
точку О, не совпад. С центром масс С
тела), видим, что если приведенная
длина L
физического маятника равна длине
математического маятника, то периоды
колебаний этих маятников одинаковы.
Следовательно, приведенная длина
физ. Маятника- длина такого
математического маятника, период
колебаний которого совпадает с
периодом колебаний данного физического
маятника.