§13. Колебательные режимы протекания химических реакций.При описании процесса окисления высших углеводородов используется модельная схема. Схема Вольтера:

1) ,

2) ,

3) .

1) Из исходного вещества A авто-каталитически образуется проме-жуточный продукт M₁.

2) Аналогично из M₁ образуется промежуточный продукт M₂.

3) Исходное вещество А взаимо-действует с M₂, и образуется про-дукт Р. В (1) и (2) также обра-зуется P. Для описания кине-тических закономерностей перей-дем к дифференциальным уравне-ниям:

, (1)

, (2)

, (3)

. (4)

Для решения этой системы най-дем некоторые закономерности. Концентрацию продукта Р можно будет определить, когда будут известны A(t), M₁(t), M₂(t). Для простоты будем полагать, что A(t)=A₀, т. е. концентрация исхо-дного вещества А не изменяется. Это справедливо либо для отк-рытых систем (вещество прихо-дит в том же количестве, в каком расходуется), либо в случае, когда вещество А находится в системе в избытке, т. е. его концентрация большая, и в процесса эта конце-нтрация меняется незначительно, т. е. .При таком упрощении кинетические зако-нномерности процесса будут определять уравнения (2) и (3), которые примут вид:

, (2’)

. (3’)

Система (2’), (3’) автономна, т. е. ее правая часть не зависит от времени, поэтому можно разде-лить (2’) на (3’), t исключается. Получаем ,

- уравнение с разделяющимися переменными.

,

проинтегрируем:

.

Разделим уравнение на k₃A₀:

,

проинтегрируем:

. (6)

Исследуем уравнение (6). Левая часть уравнения является функ-цией f(M₁,M₂), при чем f(M₁,M₂)0.

f(M₁,M₂)0, когда M₁0 или M₂0, или когда (M₁+M₂).

Функция f(M₁,M₂) имеет макси-мальное значение f₀(M₁₀,M₂₀) в стационарной точке системы (2’), (3’) – (M₁₀,M₂₀), т. е. когда правая часть обращается в ноль.

, . (8)

f₀(M₁₀,M₂₀) можно посчитать испо-льзуя (5) или 96).Таким образом, константа C₁ может меняться в диапазоне 0С₁f₀. Если взять из этого диапазона конкретное С₁ и построить фазовый портрет (трае-кторию) в координатах (M₁,M₂), то получится замкнутая кривая, которая внутри себя содержит стационарную точку.(рис21).

Когда на фазовом портрете полу-чаются замкнутые траектории, то физическом пространстве имеет место колебательный режим. Т. е. периодически будет наблюдаться повторение состояния системы. Обычно исследование таких ре-жимов проводится в окрестности стационарной точки. Если в окре-стности стационарной точки имеет место эллипс, то в физии-ческом пространстве наблюдают-ся гармонический колебания. Та-кая стационарная точка называет-ся стационарной точкой типа центр. Т. е. система в эту точку не попадает. Возможно поло-жение равновесия, период у M₁ и M₂ одинаковый.(Рис 22)

Если фазовый портрет имеет вид:

(рис23).То система ведет себя апе-риодически (не колеблясь), Асим-птотически приближаясь к ста-ционарному состоянию. То такая стационарная точка называется стационарной точкой типа узел.

Если фазовый портрет имеет вид:

(рис 24) То такая стационарная точка называется стационарной точкой типа устойчивый фокус. В физическом пространстве наб-людаются затухающие колебания.

Если фазовый портрет выглядит следующим образом: (рис25)

То такая стационарная точка на-зывается стационарной точкой типа неустойчивый узел. Сис-тема уходит из стационарного со-стояния апериодически.м Если фазовый портрет имеет вид: (рис25) То имеем стационарную точку типа неустойчивый фо-кус. Таким образом, по фазовому портрету можно судить о пове-дении системы во времени. Для нашей системы в окрестности стационарной точки будет эллипс, его можно получить из уравнения (5) или (6), если представить:

, , .(7) Если (7) подставить в

(5) и преобразовать, удерживая лишь главные слагаемые, то получим: ,- уравне-ние эллипса. При удалении от ста-ционарной точки, то в данном случае также наблюдаются замк-нутые траектории, что говорит о положительном изменении, но ко-лебания будут релаксационные. Метод линеаризации Рассмат-ривая поведение в окрестности стационарной точки, исследова-ние обычно проводят методом ли-неаризации, т. к. получить Инте-грал типа (5) или (6) удается не всегда.Используем систему (2’), (3’):

1) Ищется стационарная точка (их может быть несколько):

 (M₁₀,M₂₀). (рис26)

2) Исследуется поведение систе-мы (2’), (3’) в окрестности стацио-нарной точки. Поэтому переме-нные M₁ и M₂ записываются в ви-де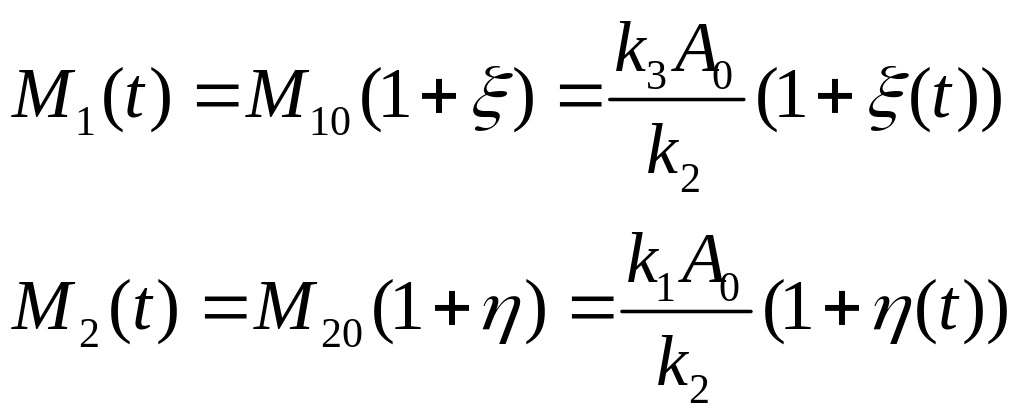(7): , . (7’).

3) (7’) подставим в систему (2’), (3’) и преобразуем. Полученное выражение, с учетом малости  и :

Разделим все на , и после преобразования получим:

Из полученной системы удержи-ваются только главные линейные слагаемые, а второй слагаемые со вторым порядком малости O(,) отбрасываются. Получаем лине-аризованную систему:

(9)Для решения систе-мы (9) продифференцируем вто-рое уравнение по времени, полу-чим

Получаем уравнение колебаний:

, с частотой колеба-ний .Решение этого уравнения имеет вид:

. (10)

С₁ и φ – константы интегри-рования, которые находятся из начальных условий. Пусть нача-льные условия: , .

Тогда , .Из (10):

, . Т. е. в окрестности стационарной точки  ведет себя следующим образом:

.(10’) Имеем незату-хающие гармонические колебания в окрестности центра. Из (9):

(11) Из (10’) и (11):

,т. е. имеем уравне-ние эллипса в чистом виде: . (12) Согласно (12) в

фазовой плоскости получили эллипс с соотношением полуосей и с центром в точке =0, =0:

.В физиче-ском пространстве при этом, согласно (10’) и (11), имеют место гармонические колебания реаген-тов M₁ и M₂ в окрестности их стационарных значений. Частота колебания зависит от констант скоростей первой и третьей стадий и от начальной концентрации исходного вещест-ва. По фазе колебания M₁ опере-жают колебания M₂ на величину /2. Соотношение амплитуд коле-баний и определяет отношение констант скоростей k₁ и k₃. Если k₁>k₃, то A(M₁)>A(M₂), и наоборот (А – амплитуда). По типу стацио-нарная точка (7) типа центр. Да-нные колебания и решения (10’), (11) имеют место лишь в окре-стности стационарной точки, пока  и  малы. Если система нахо-дится вдали от стационарной точ-ки, то колебания будут уже не гармонические, а релаксацио-нные.Рассмотренные колебания присущи различным системам: ракетные двигатели, радиотех-нические схемы, в биологических объектах, даже в численности населения и прочих социальных процессах. Особый интерес вызы-вают колебания в биологических системах. Пример: в конце XIX века в Италии Вольтером была поставлена следующая задача. Имеется местность, в которой отсутствует миграция, и в кото-рой проживают хищники рыси и жертвы зайцы. Растительная пища в избытке. Вопрос: могут ли рыси съесть всех зайцев? Эта задача аналогична (2’), (3’), A₀ – расти-тельная пища (в избытке), M₁ – численность зайцев, M₂ – числе-нность рысей. В результате 40 лет наблюдений можно было прове-рить решение этой задачи. Наб-людались колебания по числе-нности с периодом 20 лет: (рис27)

Схема Лотки.

Эта схема является вторым при-мером колебательного режима. Включает в себя три стадии:

1) ,

2) ,

3) .В первой стадии из вещества А образуется проме-жуточный продукт M₁. Во второй из M₁ автокаталитически образу-ется второй промежуточный про-дукт M₂. В третьей стадии M₂ распадается на конечный продукт P. Кинетические уравнения име-ют вид

, ,

, .

Эта система имеет первый Инте-грал, из которого можно найти концентрацию продукта P. И ре-шение будут определять первые три уравнения. Для простоты исследования будем считать A=A₀. Тогда поведение системы будут определять уравнения:

, (13)

. (14)

Исследуем (13), (14) методом линеаризации в окрестности ста-ционарной точки. Найдем стацио-нарную точку:

, ,Отсюда полу-чаем получаем одну стациона-рную точку:

, . (15)

Решение ищем в виде:

, ,(16)

где ,<<1. Подставим (16) в (13), (14):

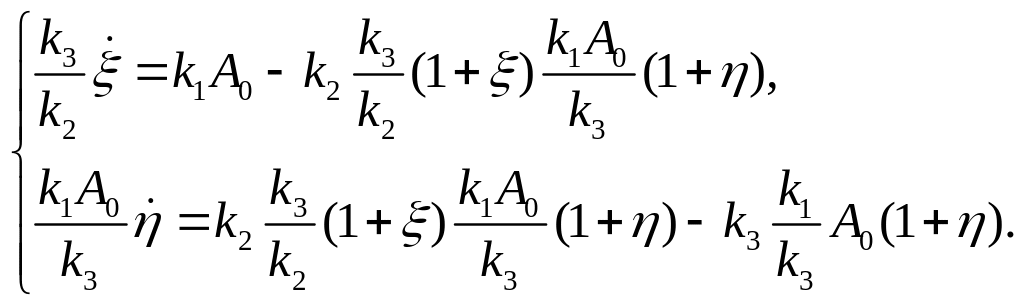
Из этой системы путем преоб-разований получаем:

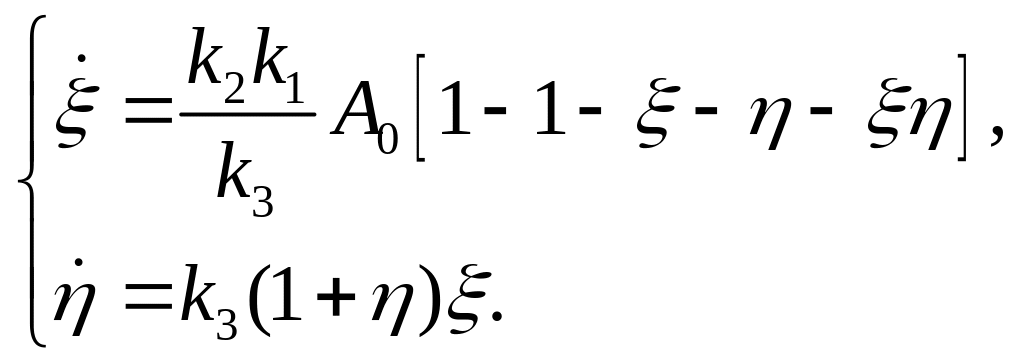Проведем линеаризацию. Удер-жим слагаемые только первого порядка малости:

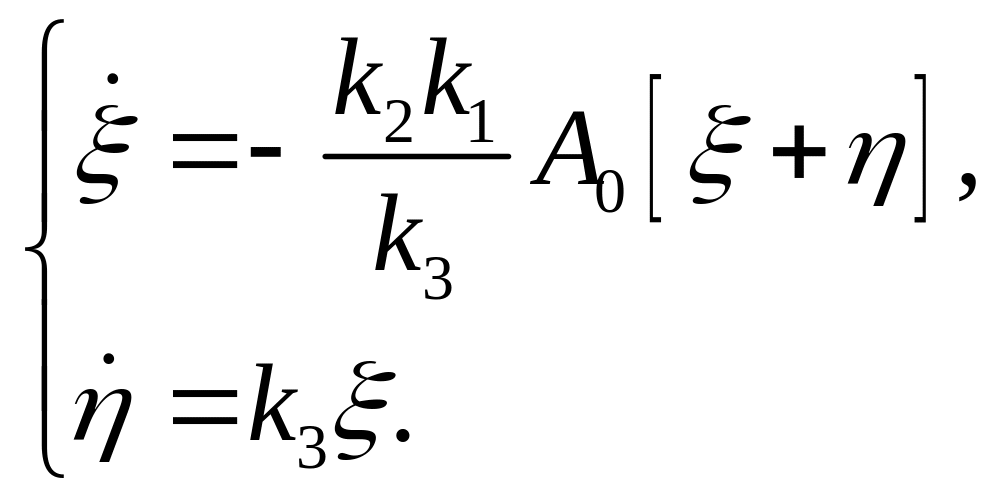(17)

Решим систему (17). Продиф-ференцируем первое уравнение:

.Введем обозначение: , .

Тогда уравнение для  примет вид: . (18)

Полученное уравнение является уравнением для затухающих коле-баний, где  - декремент затуха-ния. Решение этого уравнения имеет вид: , (19)

где . Получаем усло-вие колебаний в безразмерном ви-де: . (20) Или, если перейти к размерным переме-нным: . (20’)

Таким образом, решение можно записывать в виде (19) только в том случае, если выполняется условие (20’). Константы С₁ и φ определяются из начальных условий: , .

определим из первого уравнения (17): (рис28)

(21)

Подставим (19) в (21), получим:

Следовательно:

(*)Из последней системы: , .С₁ получим из второго уравнения (*): .

Тогда , .Определим выражение для . Из первого уравнения (17):

где , .

Такой угол существует, так как выполняется соотношение .Тогда . (25) С учетом последних преоб-разований:

Получаем в итоге (24) где , ψ опреде-ляется из (25).При выполнении (20’) в окрестности стационарной точки (16) имеют место затуха-ющие колебания с логарифми-ческим декрементом затухания:

.Если декремент затуха-ния мал T<<1, где Т – период колебаний: ,то затухание не-значительно. При этом: ,  , и . Тогда , и .Т. е. коле-бание  по фазе опережают коле-бания  на угол ₁, который при малом декременте затухания близок к /2. Следовательно, колебания при малом декременте затухания будут почти гармони-ческие с таким же сдвигом по фа-зе, как и в схеме Вольтера. По ам-плитуде колебания  и  соот-носятся как

Т. е. в зависимости от соот-ношений k₁ и k₂ а также от нача-льной концентрации A₀, ампли-туды могут соотноситься между собой по-разному. Если декре-мент затухания мал, то А_>>А_. Если условие колебания (20’) не выполняется, то колебания отсут-ствуют, и в окрестности стацио-нарной точки наблюдается апери-одическое движение в сторону стационарной точки. , (26)

,С₁, С₂ находятся из начальных условий. Аналогичный вид имеет выражение для (t). Стационарная точка (16) при выполнении (20’) является стационарной точкой типа устойчивый фокус. Тогда в фазовом и физическом прост-ранстве будем наблюдать следую-щую картину: (рис29)

В случае невыполнения (20’) ста-ционарная точка является стацио-нарной точкой типа устойчивый узе(рис30)