
- •§1. Макрокинетическая система.
- •§2. Основные задачи химической кинетики.
- •§3. Скорость химической реакции.
- •§4. Скорость простых химических превращений.
- •5. Реакции нулевого порядка.
- •§7. Последовательные реакции.
- •§8. Параллельные реакции.
- •§11. Кинетические уравнения обратимого химического проце-сса.Пусть имеем простую реак-цию:
- •§13. Колебательные режимы протекания химических реакций.При описании процесса окисления высших углеводородов используется модельная схема. Схема Вольтера:
- •§14. Элементарные понятия теории цепных реакций.
- •4. Стадия разветвления цепей.
- •§16. Окисление водорода при низком давлении, как пример црр.Рассмотрим одну из наибо-лее интересных реакций: окисле-ние водорода. Это высокоэнерге-тическая реакция.
- •§19. Элементы теории соударений.Данная теория была разработана и нашла широкое применение для газофазных реакций.
§11. Кинетические уравнения обратимого химического проце-сса.Пусть имеем простую реак-цию:
![]() ,
,![]() – стехиометрические коэффициен-ты.
Поскольку реакция простая, то, согласно
уравнению, можно составить пропорцию
по измене-нию концентраций участвующих
веществ:
– стехиометрические коэффициен-ты.
Поскольку реакция простая, то, согласно
уравнению, можно составить пропорцию
по измене-нию концентраций участвующих
веществ:![]() .Получаем
m+l
равенств. Продиффере-нцируем:
.Получаем
m+l
равенств. Продиффере-нцируем:![]() .
Согласно закону действующих масс
.
Согласно закону действующих масс
![]() (произведение по всем i).Де-Донде
предложил для исследования процесса
Рас-смотреть величину x,
которому равна первая пропорция (1). x
ха-рактеризует ход процесса, опреде-ляя
насколько глубоко прошла ре-акция. В
начале процесса x=0,
а далее x
будет возрастать. В отли-чие от глубины
превращения x
яв-ляется размерной величиной и
соответствует размерности конце-нтрации.
Зная x,
можно найти все A,
и все B.
(произведение по всем i).Де-Донде
предложил для исследования процесса
Рас-смотреть величину x,
которому равна первая пропорция (1). x
ха-рактеризует ход процесса, опреде-ляя
насколько глубоко прошла ре-акция. В
начале процесса x=0,
а далее x
будет возрастать. В отли-чие от глубины
превращения x
яв-ляется размерной величиной и
соответствует размерности конце-нтрации.
Зная x,
можно найти все A,
и все B.
![]() Уравнение
для x
найдем из (2), подставив
или
Уравнение
для x
найдем из (2), подставив
или
![]()
![]() .Реакция
может идти как в прямом, так и в обратном
направлении. Только при различных
темпера-турах состояние химического
рав-новесия может быть смещено либо в
сторону продуктов, либо в сторону
исходных веществ. То ес-ть, если при
химическом равнове-сии продуктов почти
нет, то гово-рят, что реакция не идет
(хими-ческое равновесие смещено в
сто-рону исходных веществ). Если при
химическом равновесии ис-ходных веществ
практически нет, то говорят, что химическая
реак-ция идет до конца (химическое
равновесие смещено в сторону продуктов).В
зависимости от температуры, химическое
равно-весие может изменяться, и при
определенных температурах, в состоянии
равновесия, в смесях могут быть и исходные
вещества, и продукты. Рассмотрим
законно-мерности
химического процесса:
.Реакция
может идти как в прямом, так и в обратном
направлении. Только при различных
темпера-турах состояние химического
рав-новесия может быть смещено либо в
сторону продуктов, либо в сторону
исходных веществ. То ес-ть, если при
химическом равнове-сии продуктов почти
нет, то гово-рят, что реакция не идет
(хими-ческое равновесие смещено в
сто-рону исходных веществ). Если при
химическом равновесии ис-ходных веществ
практически нет, то говорят, что химическая
реак-ция идет до конца (химическое
равновесие смещено в сторону продуктов).В
зависимости от температуры, химическое
равно-весие может изменяться, и при
определенных температурах, в состоянии
равновесия, в смесях могут быть и исходные
вещества, и продукты. Рассмотрим
законно-мерности
химического процесса:
– в пря-мом направлении,
![]() – в обрат-ном
направлении.Скорость хи-мического
процесса ω,
будет оп-ределяться суммой скоростей,
с учетом направления:
– в обрат-ном
направлении.Скорость хи-мического
процесса ω,
будет оп-ределяться суммой скоростей,
с учетом направления:
![]() .
Если наступит химическое равно-весие,
то суммарная скорость ω=0,
тогда:
.
Если наступит химическое равно-весие,
то суммарная скорость ω=0,
тогда:
![]() (4)
(4)![]() – концентрации, в состоянии хими-ческого
равновесия. Равновесные процессы
изучаются в равновесной термодинамике.
Термодинамичес-кая константа равновесия
– концентрации, в состоянии хими-ческого
равновесия. Равновесные процессы
изучаются в равновесной термодинамике.
Термодинамичес-кая константа равновесия
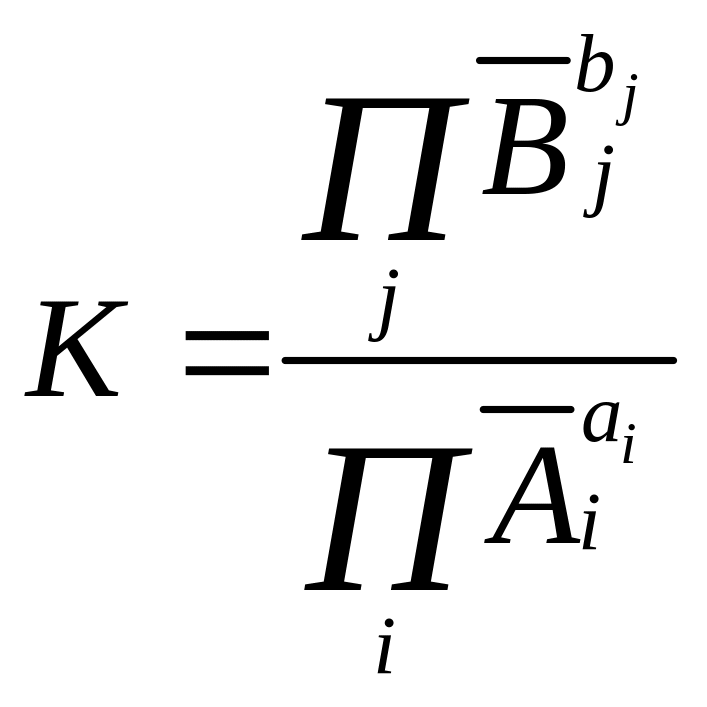 .Согласно (4),
конст-анта
.Согласно (4),
конст-анта
![]() .Т.
о., если реакция простая, то её константа
равнове-сия равна отношению констант
скоростей прямой и обратной реа-кции.
Кинетические закономерно-сти обратимого
процесса удобно определять через x.
Уравнение д-ля x
определяется также из (2), но вместо ω,
подставляется ω
с уче-том прямой и обратной реакции. Для
x
получаем уравнение:
.Т.
о., если реакция простая, то её константа
равнове-сия равна отношению констант
скоростей прямой и обратной реа-кции.
Кинетические закономерно-сти обратимого
процесса удобно определять через x.
Уравнение д-ля x
определяется также из (2), но вместо ω,
подставляется ω
с уче-том прямой и обратной реакции. Для
x
получаем уравнение:
![]()
(3’)Уравнение (3’) – обыкновен-ное дифференциальное уравне-ние, с разделяющимися перемен-ными, и его можно разрешить до квадратур. Рассмотрим кинетиче-ские закономерности для простой об-ратимой химической реакции 1-го порядка.
Т огда урав-нение (3‘) принимает вид:
![]() ,
,
![]() (3’’)
(3’’)
– линейное неоднородное диффе-ренциальное уравнение. Началь-ные условия x(0)=0
![]() (5Разделим
на
(5Разделим
на
![]() .
.
![]() (5’).
(5’).
Из решения (5’)
видно, что пере-менная x
ведет себя так же, как концентрация
продукта в случае простой реакции 1-го
порядка, то-лько вместо константы
скорости стоит сумма констант скоростей
прямой и обратной реакции
![]() .
.
При t→∞,
система стремится к равновесному
состоянию, и
![]() .
.
![]() .Если
подставить
.Если
подставить
![]() в выражения для A
и B,
то получим их равновесные значения:
в выражения для A
и B,
то получим их равновесные значения:
![]() (
(![]() ,
,![]() )
)![]() ,
,
![]() .
.
Симметричный вид,
и если
![]() ,
тогда B
будет исходным веществом, A
продуктом. Т.е. для обратимого процесса
трудно ска-зать, что будет исходным
вещес-твом, а что продуктом.Изменение
во времени:
,
тогда B
будет исходным веществом, A
продуктом. Т.е. для обратимого процесса
трудно ска-зать, что будет исходным
вещес-твом, а что продуктом.Изменение
во времени:
![]()
![]() (6)
(6)
![]() (7)
(7)
(6), (7) – кинетические
кривые.Т. о., для обратимых химических
процессов, как исходное вещес-тво, так
и продукт ведут себя по-добно соответствующим
вещес-твам для реакции 1-го порядка, но
изменение во времени происходит в
соответствии с константой
![]() .По
экспериментальным данным можно определить
конст-анту прямой
.По
экспериментальным данным можно определить
конст-анту прямой
![]() и обратной реа-кции
,
если результаты экспе-римента обработать
в переменных
и обратной реа-кции
,
если результаты экспе-римента обработать
в переменных
![]() Согласно
(5’)
Согласно
(5’)
![]() ,
,
x можно измерить.(рис20)
Когда система
приходит в равно-весие:![]() ,
следовательно, найдем
и
.Аналогично
обра-батываются результаты более
вы-соких порядков.
,
следовательно, найдем
и
.Аналогично
обра-батываются результаты более
вы-соких порядков.
12. Метод квазистационарных концентраций. Формализм ме-тода.В ряде случаев получить то-чное решение кинетических урав-нений не удается. Возможна такая ситуация, что точное решение по-лучено, но использовать его для анализа невозможно, тогда испо-льзуются приближенные методы решения. В частности, в химичес-кой кинетике широко распростра-нен метод квазистационарных ко-нцентраций. Рассмотрим форма-льную сторону метода на примере образования бромистого водоро-да:
![]() ,Однако
экспе-римент показывает другую
кине-тическую скорость:
,Однако
экспе-римент показывает другую
кине-тическую скорость:
![]() ,(*)т.
е. ско-рость зависит еще и от продукта.
Все это указывает на сложный ме-ханизм
химического процесса. Он проходит в 5
стадий:
,(*)т.
е. ско-рость зависит еще и от продукта.
Все это указывает на сложный ме-ханизм
химического процесса. Он проходит в 5
стадий:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
(Реакции 1 и 5, а также 2 и 4 вза-имообратные) Если определять скорость образования продукта по данному механизму, то получим
![]() (1)Скорость образования
проду-кта зависит от концентраций
про-межуточных продуктов.
(1)Скорость образования
проду-кта зависит от концентраций
про-межуточных продуктов.
![]() (2)
(2)
![]()
![]() (3)
(3)
![]() ,
,
![]() ,
тогда
,
тогда
![]() (2’)
(2’)
![]()
![]() (3’)
(3’)
Даже если считать,
что концент-рации исходных веществ H2
и Br2
не меняются, то все равно получа-ется
сложная система, которую сложно разрешить.
Для данной системы используется
приближе-ние. Дело в том, что промежу-точные
продукты H
и Br
очень активны, поэтому в ходе химии-ческого
процесса они сразу всту-пают во
взаимодействие распада, и их концентрация
на протяжении всего процесса очень
мала, сле-довательно, ее можно считать
по-стоянной. Такое состояние назы-вается
квазистационарным
сос-тоянием.
Концентрации H
и Br
будут меняться только за счет изменения
концентрации исход-ных веществ. Спустя
небольшой промежуток времени в
реагирую-щей системе устанавливается
ква-зистационарное состояние, поэто-му
эти концентрации можно най-ти. Решаем
(2) и (3), сложим (2’) и (3’):
![]() .
.
Это уравнение соответствует хи-мическому равновесию 1-ой и
5-ой стадий, следовательно
![]() .Концентрацию
во-дорода можно найти из (2’), под-ставим
(4) в (2’):
.Концентрацию
во-дорода можно найти из (2’), под-ставим
(4) в (2’):
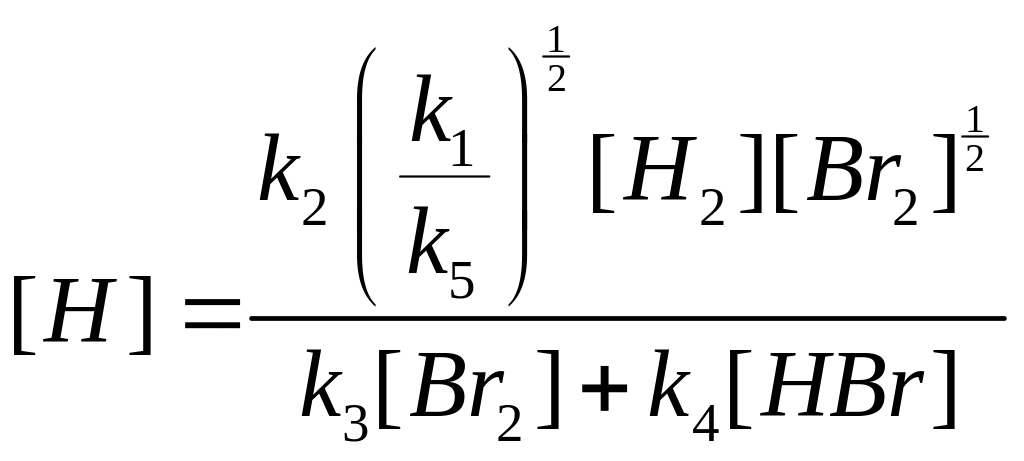 .
(5)
.
(5)
Необходимо получить
![]() ,
,
т. е. как изменяется концентрация продукта. Для этого в (1) под-ставляем [H], [Br] и используем (2). Из (2’):
![]() ,.
,.![]()

 .(6)Получили
выражение (6) для скорости образования
продукта, которое качественно согласуется
с экспе-риментальными данными по этой
величине, т. е. с (*).Это качест-венное
согласование зависимости скорости
реакции от концент-раций
.(6)Получили
выражение (6) для скорости образования
продукта, которое качественно согласуется
с экспе-риментальными данными по этой
величине, т. е. с (*).Это качест-венное
согласование зависимости скорости
реакции от концент-раций
![]() указы-вает на правильность сделанных
допущений, положенных в основу метода.Как
видно из (6) фор-мальные экспериментальные
па-раметры
указы-вает на правильность сделанных
допущений, положенных в основу метода.Как
видно из (6) фор-мальные экспериментальные
па-раметры
![]() и m
зависят от всех скоростей стадий
процесса: k1,
k2,
k3,
k4
и k5.
Математическую осно-ву метода
квазистационарных ко-нцентраций
составляет асимпто-тический характер
данной задачи, который лучше прослеживается
по системе:
и m
зависят от всех скоростей стадий
процесса: k1,
k2,
k3,
k4
и k5.
Математическую осно-ву метода
квазистационарных ко-нцентраций
составляет асимпто-тический характер
данной задачи, который лучше прослеживается
по системе:
![]() ,
,
![]() ,
ε<<1.
,
ε<<1.
Если x, y – искомые функции, а t – независимая переменная, то
![]() ,
,
![]() .
Все величины по-рядка единицы. Если f0,
то f/ε>>φ,
т. е. скорость изменения y
будет бесконечно большой при ε0,
по сравнению со скоростью изменения x.
Поэтому, вначале быстро изменяется y,
а x
прак-тически не изменяется. Так будет
до тех пор, пока f
не станет нулем. При f=0
y
не меняется. Меняется медленно x,
до тех пор, пока f0,
тогда опять происходит быстрое изменение
y,
а x
почти не изменяется и опять f=0,
и т. д.
.
Все величины по-рядка единицы. Если f0,
то f/ε>>φ,
т. е. скорость изменения y
будет бесконечно большой при ε0,
по сравнению со скоростью изменения x.
Поэтому, вначале быстро изменяется y,
а x
прак-тически не изменяется. Так будет
до тех пор, пока f
не станет нулем. При f=0
y
не меняется. Меняется медленно x,
до тех пор, пока f0,
тогда опять происходит быстрое изменение
y,
а x
почти не изменяется и опять f=0,
и т. д.
Квазистационарное состояние быстрых переменных устанав-ливается в системе спустя неко-торый промежуток времени t1, поэтому при 0<t<t1 полученные формулы неприменимы (в строгом асимптотическом под-ходе формулы, которые будут описывать процесс в начальной стадии).
