
- •§1. Макрокинетическая система.
- •§2. Основные задачи химической кинетики.
- •§3. Скорость химической реакции.
- •§4. Скорость простых химических превращений.
- •5. Реакции нулевого порядка.
- •§7. Последовательные реакции.
- •§8. Параллельные реакции.
- •§11. Кинетические уравнения обратимого химического проце-сса.Пусть имеем простую реак-цию:
- •§13. Колебательные режимы протекания химических реакций.При описании процесса окисления высших углеводородов используется модельная схема. Схема Вольтера:
- •§14. Элементарные понятия теории цепных реакций.
- •4. Стадия разветвления цепей.
- •§16. Окисление водорода при низком давлении, как пример црр.Рассмотрим одну из наибо-лее интересных реакций: окисле-ние водорода. Это высокоэнерге-тическая реакция.
- •§19. Элементы теории соударений.Данная теория была разработана и нашла широкое применение для газофазных реакций.
§7. Последовательные реакции.
Дифференциальные уравнения, описывающие кинетику протека-ния последовательных реакций второго и более высокого поря-дка, являются нелинейными. По-этому их решение в большинстве случаев аналитически получить не удается.Рассмотрим две по-следовательные реакции 1-го по-рядка. Схема процесса:
![]() ,
,
Несмотря на простоту, эта схема позволяет определить основные качественные закономерности по-следовательных реакций.
![]() (зависит
от концент-рации промежуточного
продукта)(1) (1)
(зависит
от концент-рации промежуточного
продукта)(1) (1)
![]() (зависит
от конце-нтрации исходного вещества)(2) (2)
(зависит
от конце-нтрации исходного вещества)(2) (2)
![]() (3)
(3)
Начальные условия:
,
![]() .
.
Получим первый интеграл сис-темы, сложим (1), (2) и (3):
![]() ,
,
следовательно, получаем
![]() ,
(4)
,
(4)
![]() , (4’)т.о.
продукт можно найти, если знать
концен-трации A
и M.
Чтобы из (2) найти M,
необходимо найти A,
для этого решим уравнение (3):
, (4’)т.о.
продукт можно найти, если знать
концен-трации A
и M.
Чтобы из (2) найти M,
необходимо найти A,
для этого решим уравнение (3):
![]() . (5)
. (5)
Подставим найденное
значение в (2):![]()
– линейное
неоднородное диффе-ренциальное уравнение
1-го по-рядка, его решение складывается
из общего решения однородного уравнения
и частного решения неоднородного:![]() .(k1≠k)
.(k1≠k)
Используя начальные
условия, находим C2,
и получаем:
![]() .(6)
.(6)
(5) и (6) подставим в (4’), получим изменение концентрации продукта P:
![]() (7).Таким
образом, получены кинетические кривые
для всех веществ (A,
M,
P),
для случая
(7).Таким
образом, получены кинетические кривые
для всех веществ (A,
M,
P),
для случая
![]() .Рассмотрим
особый случай k1=k2=k.
Тогда решение можно по-лучить из (5) и
(6). В (6) неопре-деленность раскроем по
правилу Лапиталя:
.Рассмотрим
особый случай k1=k2=k.
Тогда решение можно по-лучить из (5) и
(6). В (6) неопре-деленность раскроем по
правилу Лапиталя:
![]()
![]()
Таким образом, для
вещества M
получили: ![]() . (6’)
. (6’)
Для продукта
P: ![]() . (7’)
. (7’)
Поскольку полученные кинетиче-ские кривые асимптотически стремятся к 0 лишь при t→∞, то время полного химического пре-вращения = ∞.Однако, можно отметить два характерных вре-мени: 1. Время полупревращения по исходному веществу:
,
(когда
![]() порядка
порядка
![]() ).
(рис12)
).
(рис12)
2.Интересно ведет
себя проме-жуточный продукт. Можно найти
время, когда он достигает макси-мального
значения, продиффере-нцировав (6) или
(6’): ![]() ,
,
![]() близко к
близко к
![]() ,
соотве-тственно
,
соотве-тственно
![]() – среднее время жизни по исходному
веществу
– среднее время жизни по исходному
веществу
![]() ,
,
т. е. согласно (5’) в точке мак-симума A и M совпадают.
Если использовать
уравнение (6), когда
,
то 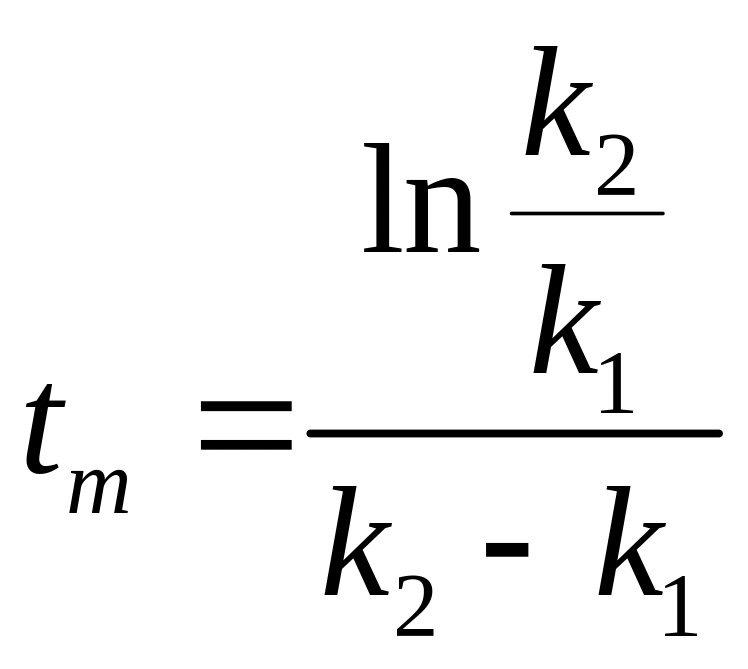 .
.
Значение максимальной
концент-рации промежуточного продукта
M: 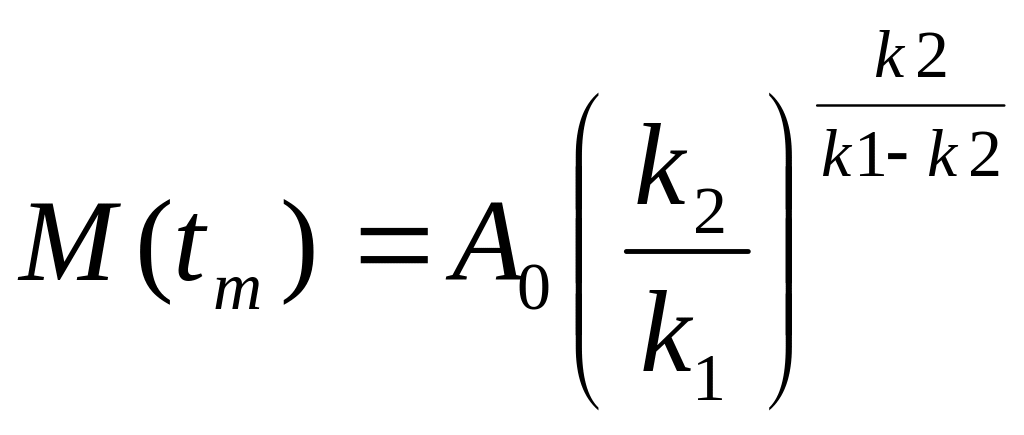 .
.
![]() и
и
![]() зависят от со-отношения
и
:
>
или
<
.
зависят от со-отношения
и
:
>
или
<
.
Можем использовать (7) или (7’): .
Так как M≥0,
то кривая P(t)
монотонно-возрастающая. Кривизна:![]()
– перегиб достигается
в момент
![]() ,
где
,
где
![]() – время, когда ко-нцентрация промежуточного
про-дукта максимальна.
– время, когда ко-нцентрация промежуточного
про-дукта максимальна.![]() ,
при
,
при
![]() ;
;![]() ,
при
,
при
![]() .
.
Следовательно, в
точке перегиба кривизна кривой P(t)
переходит с положительной на отрицатель-ную,
а сама кривая имеет S-фо-рму.
(рис13)
![]() (нем-ного ниже) Рассмотрим два преде-льных
слу-чая: 1.k1>>k2
.Это
означает, что всё исходное вещество с
большой скоростью, по сравне-нию со
второй стадией проце-сса, перейдет из
исходного веще-ства A
в вещество M.
После этого будет происходить медле-нное
превращение, по сравнению с первой
стадией, вещества M
в конечный продукт P.
(нем-ного ниже) Рассмотрим два преде-льных
слу-чая: 1.k1>>k2
.Это
означает, что всё исходное вещество с
большой скоростью, по сравне-нию со
второй стадией проце-сса, перейдет из
исходного веще-ства A
в вещество M.
После этого будет происходить медле-нное
превращение, по сравнению с первой
стадией, вещества M
в конечный продукт P.
Получаем:
![]() ,
,
![]()
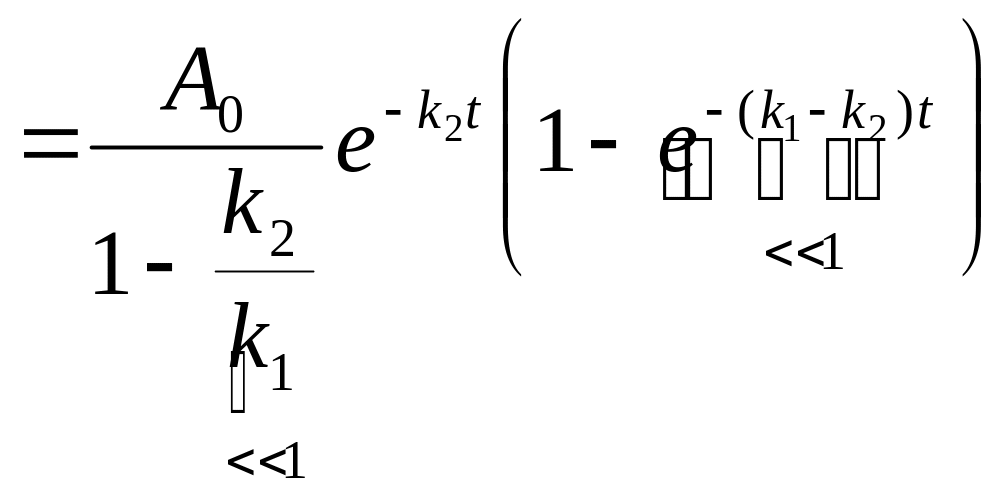
![]() ,
следовательно, в преде-льном случае M
ведет себя как исходное вещество.
(рис14).
,
следовательно, в преде-льном случае M
ведет себя как исходное вещество.
(рис14).
M(0)=0,M(0)=A0
Значение M(t)
приближенно и не точно в начальный
момент вре-мени, когда происходит
преоб-разование вещества A
в M.
Зна-чение M(t)
определяется точно по-сле установления
процесса, и мак-симум M
смещен к начальной ста-дии процесса, т.
е. tm
мало.При та-ком соотношении констант
k1
и k2,
для последовательных реак-ций, можно
выделить ведущую стадию процесса. Этой
стадией является наиболее медленная
стадия, она тормозит весь процесс.
Закончится химический процесс по
завершению второй стадии. 1.
k1<<k2
При таком со-отношении констант также
можно получить приближенную форму-лу.
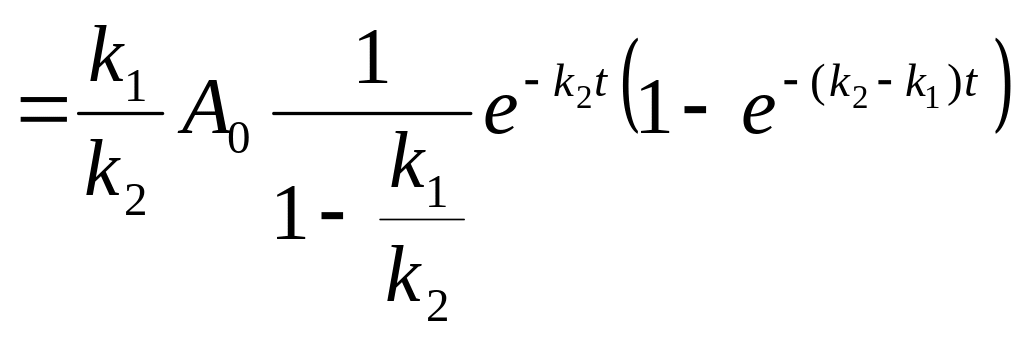
![]() Т.
е. проме-жуточный продукт M
в системе будет находиться в малых
коли-чествах, в течение всего процесса,
т. к.
Т.
е. проме-жуточный продукт M
в системе будет находиться в малых
коли-чествах, в течение всего процесса,
т. к.
![]() .
Также в системе быстро устанавливается
равно-весие между концентрацией
исхо-дного вещества и промежу-точного
продукта. Говорят, что M(t)
будет находиться в квазиста-ционарном
состоянии, т. е. его из-менение происходит
только бла-годаря изменению A(t).
Эти осо-бенности связаны с большой
ак-тивностью M.(рис15).
Сначала идет установление процесса,
смещено к началу процесса. На таких
особенностях основан ме-тод квазистационарных
концент-раций. При таком соотношении
констант ведущей стадией проце-сса
является более медленная стадия (первая),
она тормозит весь процесс, следовательно,
оп-ределяет его. Для последователь-ных
реакций ведущей стадией процесса
является самая медле-нная.
.
Также в системе быстро устанавливается
равно-весие между концентрацией
исхо-дного вещества и промежу-точного
продукта. Говорят, что M(t)
будет находиться в квазиста-ционарном
состоянии, т. е. его из-менение происходит
только бла-годаря изменению A(t).
Эти осо-бенности связаны с большой
ак-тивностью M.(рис15).
Сначала идет установление процесса,
смещено к началу процесса. На таких
особенностях основан ме-тод квазистационарных
концент-раций. При таком соотношении
констант ведущей стадией проце-сса
является более медленная стадия (первая),
она тормозит весь процесс, следовательно,
оп-ределяет его. Для последователь-ных
реакций ведущей стадией процесса
является самая медле-нная.
