5. Реакции нулевого порядка.

Было показано, при каких условиях, происходит формаль-ное понижение порядка реакции. Для этого изменение одного из исходных веществ должно быть мало существенным по сравне-нию с его начальным значением. Если изменение концентрации всех исходных веществ не сущес-твенно по сравнению с их началь-ными концентрациями, то можно формально говорить о реакции нулевого порядка, поскольку в этом случае скорость реакции практически не будет зависеть от концентрации исходных веществ. Реально это возможно в двух слу-чаях:

1).если рассматривается химичес-кий процесс при , т. е. в начале химического процесса. Очевидно, при таких t, изменение концентрации исходных веществ незначительно. Поэтому, если ха-рактерное время задачи много меньше характерного времени хи-мического процесса, то допусти-мо использовать модель реакции нулевого порядка. Это часто ис-пользуется в теории зажигания.

2).если рассматривается открытая система, и в неё извне поступает ровно столько исходного вещест-ва, сколько было израсходовано в химическом процессе, то концент-рация исходного вещества остает-ся неизменной, следовательно, скорость реакции не будет меня-ться при T=const, и имеем реак-цию нулевого порядка. Модель реакции нулевого порядка полу-чается из уравнения (12). Обоз-начим расход вещества , причем этот расход мал, т. е. 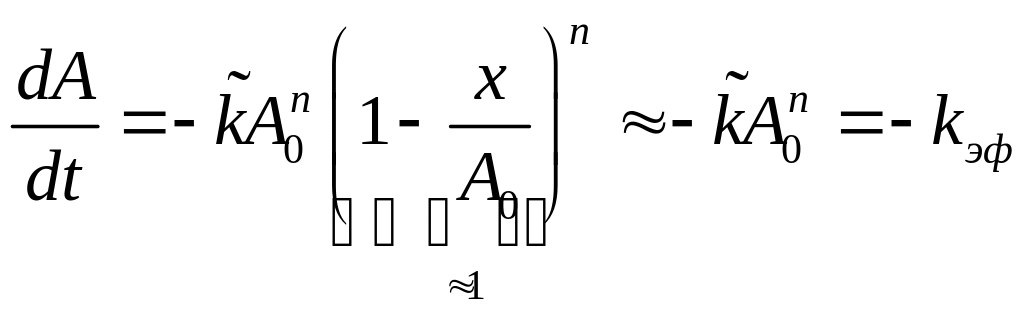, тогда , и из (12) получаем: , , (13)(рис9)

– формально.

6. Глубина выгорания. Кине-тическое подобие. При решении задач химической кинетики удо-бно ввести безразмерные переме-нные. Вводится следующая без-размерная концентрация , η – глубина превращения, в ходе химичес-кого процесса 0≤η≤1. По величине η удобно следить за ходом процесса (m – масса вещества A).

Уравнение (12), с использованием η принимает вид: .

Перейдем к безразмерному вре-мени: ,т. е. за масш-таб времени взята величина про-порциональная характерному вре-мени реакции. Получаем уравне-ние в безразмерном виде уравнение простой реакции n-го порядка. (14)

– безразмерная скорость простой реакции n-го порядка.

Если выразить через η, то (14’) В безраз-мерном виде скорость определя-ется только порядком реакции, т. е. говорят, что все простые реак-ции конкретного порядка между собой кинетически подобны. Это подобие определяется порядком реакции. Поэтому очень удобно описывать процесс в безразмер-ном виде, так как решается не одна, а множество кинетически подобных задач. (рис10). Таким образом, для всех реакций n-го порядка, при , в ходе хи-мического процесса, скорость монотонно уменьшается от 1 до 0. И только при n=0 (реакция нуле-вого порядка), скорость реакции неизменна (безразмерная скорость ).Если решить задачу (14), то получим поведение глубины пре-вращения η(τ) для кинетически подобных систем.

(рис11).Т. е. только для реакции нулевого порядка процесс закан-чивается в конечный момент вре-мени, для остальных реакций при τ→∞, кривая асимптотически стремится к 1. Таким образом, ра-ссмотрели закономерности прос-той реакции, поведение скорости простой реакции и кинетических кривых. С математической точки зрения необходимо было решать обыкновенные дифференциаль-ные уравнения, и при решении на-до отмечать:

1).существование решения;

2).единственность решения;

3).устойчивость решения;

4).получающуюся структуру (ре-жим решения); При рассмотрении простых случа-ев таких вопросов не возникало. В более сложных задачах требуются дополнитель-ные исследования.С химической и физической точки зрения, необхо-димо также определять константы скоростей реакции и механизмы химических реакций. Это решает-ся с помощью эксперимента, где выясняется, какие вещества при-сутствуют в ходе химического процесса, определяется механизм реакции по оптимальному усло-вию прохождения процесса. А математическая обработка резуль-татов эксперимента позволяет на-ходить константы скоростей хи-мических реакций.

§6. Системы кинетических ура-внений химического процесса, состоящего из нескольких эле-ментарных стадий.Перейдем к изучению сложных химических процессов.Опыт показывает, что лишь в частных случаях химичес-кий процесс следует брутто урав-нению. Обычно реакция выбирает оптимальный путь прохождения, включающий образование проме-жуточных продуктов. Это проис-ходит даже в том случае, когда исходными являются одна или две частицы. Пример: реакция присоединения молекулярного хлора к этилену. По данному механизму реакция никогда не проходит, это энергетически за-прещено. Если на систему подейс-твовать таким образом, чтобы произошло разложение Cl₂ на ато-мы, то тогда очень быстро реак-ция проходит по цепному меха-низму. Таким воздействием мо-жет быть, например, освещение системы.1) ;

2) ;

3) ;

4) ;

5) ;

6) .(точка означа-ет наличие свободной валент-ности, h_ν – квант света, атомы хлора легко вступают во взаимо-действие)Получим необходимое соотношение, если подвести бала-нс, сложив последовательно все уравнения (первое уравнение умножив на 7, второе – на 4, C₄H₈Cl₂ – дополнительный про-дукт, который можно не учиты-вать ввиду его небольшого коли-чества). Данный механизм подт-вержден с помощью эксперимен-тальных данных и энергетически он наиболее приемлем. Пример: реакция окисления водорода: включает 60 ста-дий и обладает большим тепло-вым эффектом.Возникает задача: определение в случае сложного химического процесса скорости химической реакции. Для харак-теристики взаимосвязи между со-бой отдельных стадий процесса, вводятся понятия последователь-ных, параллельных и последова-тельно-параллельных реакций.

- Две простые реакции называют-ся последовательными, если продукт одной из них является исходным веществом для другой.

- Две, и более реакции называют-ся параллельными, если исход-ным веществом для них является одно и тоже вещество.

- Реакции называются последова-тельно-параллельными, если по одному веществу они последова-тельные, а по другому параллель-ные. Таким образом, различные стадии химического процесса могут быть между собой трех типов. Реакции (1) и (6) – пос-ледовательные (в любой очеред-ности как по молекулам, так и по атомам).Реакции (2) и (3) – пос-ледовательные как по радикалу, так и по атому хлора.Реакции (2) и (4) – параллельные по атому хлора, и последовательные по ра-дикалу.Реакции (4) и (5) – парал-лельные по радикалу. Скорость простой реакции может быть за-писана согласно закону дейст-вующих масс. Поскольку каждая стадия химического процесса – простая реакция, то, согласно это-му закону, можно выписать ско-рость каждой стадии:

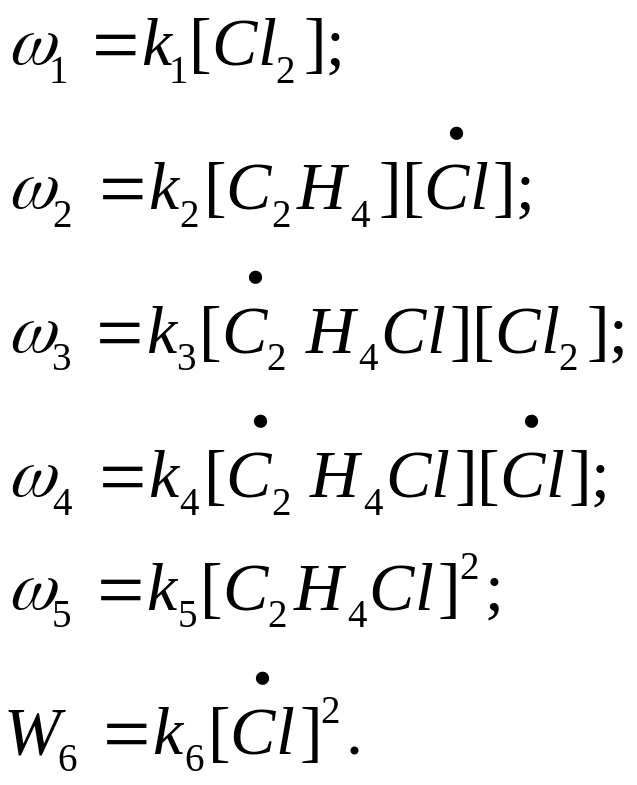
Согласно определению скорость химической реакции определяется по конкретному компоненту. В эксперименте можно следить за скоростью изменения масс отде-льных компонентов. Чтобы по-считать эту скорость через скоро-сти отдельных стадий для конк-ретного компонента, надо учиты-вать все стадии, в которых он уча-ствует с соответствующими сте-хиометрическими коэффициента-ми. Например:Скорость по моле-кулярному хлору Cl₂:

. Скорость по этилену:

Скорость по :

В общем случае, если механизм химической реакции можно запи-сать в виде: , i=1…N , j=1…K, (K уравнений)

N – количество веществ, участву-ющих в химическом процессе, включая промежуточные проду-кты. К – количество стадий хи-мического процесса. – стехио-метрические коэффициенты, если это продукт, то “+” ν, если исхо-дное вещество, то “–“ ν.

–символ соответствующей ча-стицы. Скорость j-ой стадии , скорость по i-му компоненту (по [A_i]) : – сумми-рование всех стадий, где нахо-дится компонент.

Если вещество не участвует в какой-то стадии, то в общем уравнении ее стехиометрический коэффициент в этой стадии равен нулю.