§3. Скорость химической реакции.

Определение скорости химиче-ского процесса непосредственно связано со структурой реагирую-щей системы и свойствами по-верхности, отделяющей её от ок-ружающей среды. Исходные, про-межуточные и конечные проду-кты реакции в ходе химического процесса могут находиться в различных фазовых состояниях. Поэтому различают гомогенные, гетерогенные и гомогенно-гетеро-генные реакции, и соответствую-щие им скорости. Химическая ре-акция называется гомогенной, если она протекает в пределах одной фазы. Гетерогенная реак-ция протекает на границе раздела фаз. Гомогенно-гетерогенная ре-акция – это сложный химический процесс, отдельные стадии кото-рого являются гомогенными, а другие гетерогенными реакциями.

Скорость химической реакции должна характеризовать количе-ство вещества вступающего в ре-акцию, или образующегося в ре-зультате неё. Реагирующая систе-ма состоит из совокупности Ра-зличных молекул, или их фра-гментов. Как в механике опери-руют со скоростью определенного сорта частиц, также в хим. кине-тике вводится понятие скорости хим. реакции по конкретному ко-мпоненту. Скорость химической реакции по i-му компоненту опре-деляется пропорционально скоро-сти изменения массы этого ком-понента,т.е. Коэффициент пропорциональности зависит от того, какая реакция рассматрива-ется (гетерогенная, гомогенная, гомогенно-гетерогенная). Ограничимся случаем гомогенной реакции. Для неё коэффициент пропорциональности равен:

, где V – объем реагирующей системы. , (2) Часто массу измеряют в молях, тогда , (2’) – масса i-го компонента;

– количество молей i-го компо-нента. Если в ходе химического процесса объем реагирующей системы не меняется, т. е. V=const, то скорость химической реакции будет: , (3)

– концентрация i-го компоне-нта, т. е. количество i-го компо-нента в единице объема

, .

Молярная концентрация

, .Очень часто сле-дят за скоростью изменения ко-нцентрации i-го компонента.

Скорость реакции сложных процессов.

Если i-ый компонент промежу-точный, и участвует в нескольких стадиях сложного химического процесса, то скорость реакции по этому компоненту будет вычи-сляться с учетом всех стадий, в которых он участвует.

(4)

– скорость образования, эта скорость должна учитывать все стадии, где i-ый компонент явля-ется продуктом (образуется).

– скорость расхода, эта скоро-сть должна складываться из ско-ростей всех стадий, где i-ый компонент является исходным веществом (расходуется).

В частности, если имеется обра-тимая реакция, при V =const, то можно записать .

Протекание реакции в условиях переменного объема.

Переменность объема вносит свой вклад в скорость изменения концентрации i-го компонента. ,

если перейти к концентрации, и определенной выше скорости химической реакции, то (5)

– относительная скорость изменения объема.

Таким образом, изменение конце-нтрации, при переменном объеме будет определяться скоростью хи-мического процесса и относите-льной скоростью изменения объе-ма. (5’)

Протекание реакции в движу-щейся среде.

Если реакции протекают в движу-щейся сплошной среде, то относи-тельная скорость изменения объе-ма для i-го компонента, опреде-ляется вектором скорости i-го ко-мпонента, точнее его диверген-цией: , где – ско-рость движения i-го компонента.

Кроме того, если система дви-жется, то производная

Должна пониматься в смысле Лаг-ранжа ( - изменение c_i вдоль траектории движения).

Используя данные формулы и (5’), можем получить следующие соотношения:

Таким образом, получили фор-мулу: (6)

Обычно в механике многокомпо-нентных систем стремятся из-бавиться от рассмотрения ско-ростей каждой компоненты, и перейти к скорости системы в целом:

, i=1,…,N ( - скорость движения центра масс).

Это удается сделать введением в рассмотрение диффузионных век-торов потока соответствующего компонента:

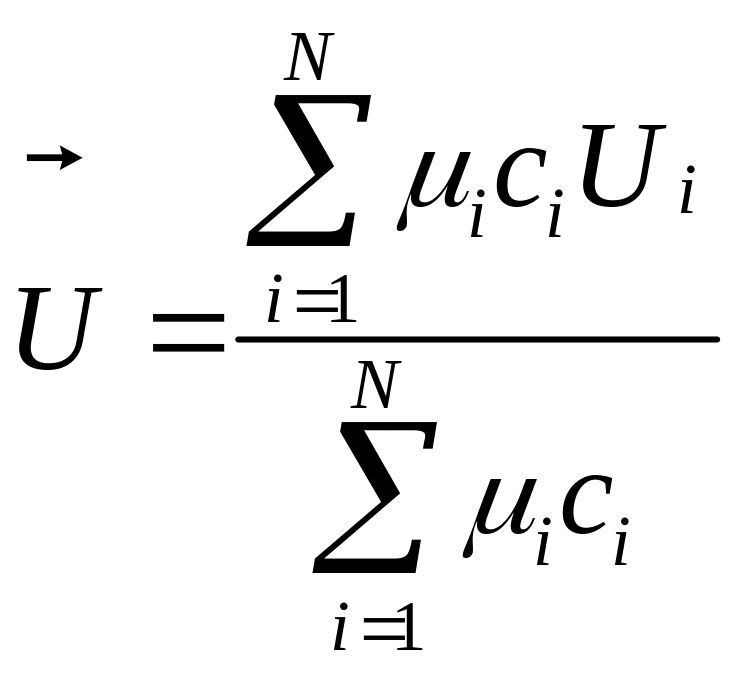, здесь – моля-рная масса i-го компонента. , т. е. скорость i-го ко-мпонента определяется диффу-зией i-го компонента и переносом его движущейся системой. Заме-тим, что процесс диффузии может присутствовать, даже если сис-тема в целом покоится, т. е. , а . Процесс диффузии отсу-тствует только если для всех ко-мпонент выполняется равенство: .Таким образом, если ввести , то (6) преобразу-ется: (7

Уравнение (7) – закон сохране-ния массы i-го компонента (урав-нение неразрывности в диффе-ренциальной форме). Концентра-ция i-го компонента изменяется за счет химического процесса, за счет дивергенции диффузионного вектора, и за счет дивергенции потока в целом. *(рис.3)

Рассмотрим объем , который ограничен поверхностью , и проинтегрируем (7) по этому объему Воспользуемся формулой Остро-градского-Гаусса: .

,

. (7’)

(7’) – закон сохранения массы i-го компонента в объеме (закон сохранения в интегральной фо-рме). Т. е. изменение массы i-го компонента происходит за счет химического процесса, за счет диффузионного потока через поверхность , и за счет потока массы i-го компонента вместе со всей движущейся системой (кон-вективный поток). Таким обра-зом, изучается , определяет-ся отдельно. Существуют феноме-нологические и статистические методы. Часто используется за-кон Фика (аналог закона Фурье для теплопроводности):

, где – коэффи-циент диффузии i-го компонента.