§19. Элементы теории соударений.Данная теория была разработана и нашла широкое применение для газофазных реакций.

Рассмотрим случай бимоле-кулярной реакции. Согласно тео-рии соударений химическое взаи-модействие происходит каждый раз, если сталкиваются молекулы нужного сорта и при этом они об-ладают энергией достаточной для преодоления потенциального бар-ьера реакции. Кроме того, они до-лжны быть ориентированны друг относительно дуга(рис41)нужным образом. При рассмотрении соу-дарения молекул считается, что они имеют форму сферы.Если ст-алкиваются молекулы А и В, то сферы будут иметь радиус r_A и r_B, соответственно. Расстояние меж-ду их центрами будет равно r_А+r_В. Отсюда можно заключить, что столкновение молекулы А с моле-кулой В произойдет, если центр молекулы В столкнется с кругом, площадь которого будет равна

S=π(r_А+r_В), а центр этого круга бу-дет лежать в центре молекулы А. Таким образом, можно сделать за-ключение о том, что В обяза-тельно столкнётся с А, если она будет находиться в цилиндричес-кой трубе радиуса R=r_А+r_В, а ось этой трубы проходит через центр молекулы А в направлении , где - скорость относительного дви-жения молекул В и А.(рис42)

Сечение данной трубы называется сечением соударения, поскольку по нему можно судить о факторе соударения. Его обозначают

Это сечение можно найти через вязкость газа. Соглас-но МКТГ вязкость: ,

где М – молярная масса газа, u – скорость движения молекул этого газа, - сечение соударения этого газа, - число Авогадро. Отсюда можно найти радиус молекул газа: . Тогда сечение соударения:

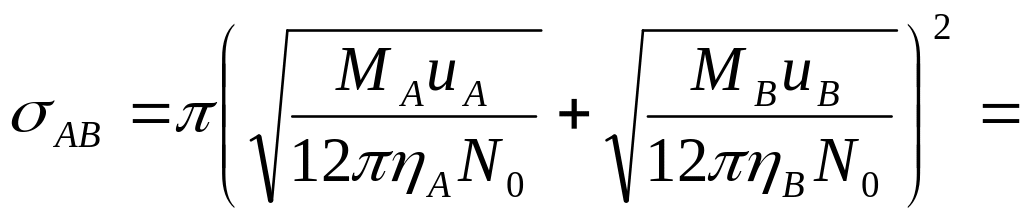
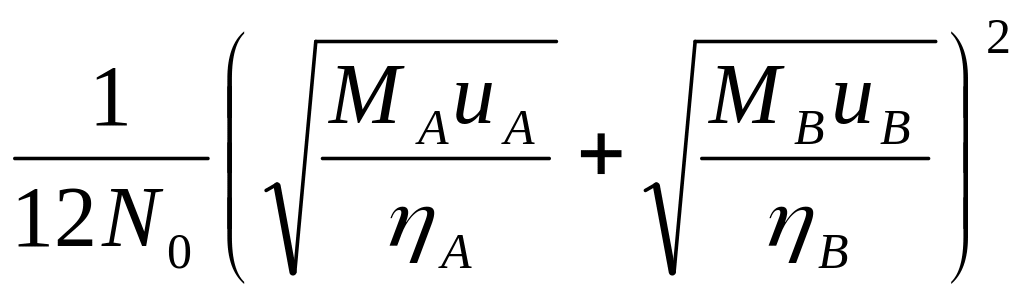В теку-щий момент времени соударение произойдет, если молекула В бу-дет находиться в указанной цили-ндрической трубе, причем на ра-сстоянии u от сечения соударен-ия, проведенного через центр мо-лекулы А.Т.о. можно посчитать объем трубы, молекулы которой столкнутся с молекулой А. С мо-лекулой А столкнутся в текущий момент времени все молекулы со-рта В, которые будут находиться в этой трубе на расстоянии u от ука-занного сечения соударения. Чис-ло соударений: ,где - концентрация молекул В.Тогда, согласно КТГ можно оценить ско-рость теплового движения:

,k – постоянная Больц-мана (переводит температуру в энергию).

- приведенная масса молекул. Общее число соударен-ий будет определяться числом со-ударений всех молекул А с молек-улами В в текущую единицу вре-мени. Чтобы получить это число, достаточно знать, сколько в един-ице объема будет молекул A.

- ко-личество соударений в единице объема молекул сорта А с моле-кулами сорта В. - фактор соударения (определяется через характеристики среды u, σ). Сог-ласно теории соударений, не все соударения приведут к химичес-кому процессу, а только те, кото-рые обладают нужной энергией для преодоления потенциального барьера реакции. Если энергия со-ударения меньше нужной энергии ( ), то соударение счита-ется упругим, и эти сферы-молек-улы потом разлетаются (энергия деформации уходит в кинетическ-ую энергию).Если энергия соуда-рения больше или равна нужной энергии ( ), то соударение считается неупругим, и происхо-дит химическое взаимодействие.В теории соударений энергия соуда-рения определяется по кинетичес-кой энергии: . - потен-циальный барьер.Чтобы опреде-лить количество эффективных со-ударений, ведущих к химическо-му процессу, воспользуемся расп-ределением Больцмана по энер-гиям: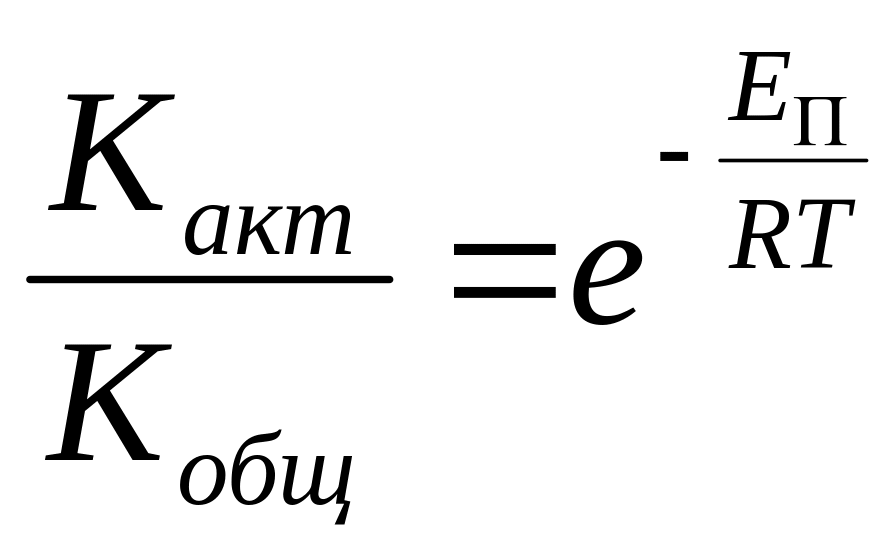 .Тогда скорость химического процесса: , .

R – универсальная газовая постоя-нная. Как было отмечено, в Тео-рии соударений учитывается, как ориентированы молекулы друг от-носиельно друга. Соударение мо-жет быть нужной энергии и нуж-ных молекул, но если при этом они неправильно ориентированы друг относительно друга, то взаи-модействия не произойдет. Это стерический фактор, вводится он через сомножитель p, 0<p<1. Тогда (1) Сог-ласно закону действующих масс, скорость химической реакции: .Сравнивая с полученой формулой (1), можно записать выражение для константы ско-рости:

(2)– константа скорости для бимо-лекулярных газофазных реакций.

- предэкспонента.

Можно провести оценку величин, входящих в (1) и (2). Из (1): .Обычно радиус молекулы , , , тогда - довольна маленькая величина.

Из теории соударений: . Тем самым отраже-но влияние температуры. Хара-ктер влияния температуры рас-смотрим на примерах.

1. Взаимодействие водорода с йодом Это газофазная бимолеку-лярная реакция.

.

По закону действующих масс

.

Согласно (2) (при н. у.) величина

большая энергия акти-вации. Посчитаем время, за кото-рое система прореагирует на 1%. При давлении 1 атм: , тогда

,(3) с точно-стью до константы. Влияние температуры:

1). Т=273°К (0°С). По формуле (3) ,

1% =1,35∙10¹⁷ шт/см³ ,

2). Т=600°К, ,

3). Т=800°К, ,

2. Взаимодействие атомов водорода Неактивированный про-цесс, сопровождается большим выходом энергии.

При давление 1 атм: , тогда

Из (2) определим k. Экспоненту не пишем, т.к. энергия активации мала. В данном случае достато-чно, чтобы частицы просто встре-тились. Посчитаем, за какое время система прореагирует на 99%. Для этого нужно решить уравне-ние:

.

Разделяя переменные и интегри-руя, получаем

,

.

Приведем к общему знаменателю и подставим выражение для концентрации:

, тогда

Управлять таким процессом сло-жно. Температура при активиро-ванном процессе влияет сущест-венным образом (пример 1), при чем основное влияние оказывает экспонента.

§20. Феноменологическая теория температурной зависи-мости константы скорости хи-мической реакции.Константа скорости химической реакции очень сильно зависит от Т, по крайней мере, для активирова-нных процессов. Опыт показы-вает, что для большинства хими-ческих реакций скорость реакции сильно зависит от Т. В связи с этим влияние Т на скорость реак-ции ω изучалось давно (с конца XIXв.) Вант-Гоффом, Аррениу-сом и другими западно-европейс-кими физико-химиками. Вант-Гофф предложил правило:

Увеличение Т на 10% приводит к увеличению ω в 10 раз. Измене-ние скорости химической реакции определяли по температурному коэффициенту, зависящему от k:

.(1) в неши-роком интервале температур не зависел от температуры, он при-нимался постоянным. Это опреде-ление было очень грубым.

В 1889г. Аррениусом была пре-дложена формула, которая опре-деляла зависимость k от T:

(2)- формула Арре-ниуса. Она была получена на основе обработки эксперимента-льных данных 6 авторов, и рабо-тала лучше предложенных дру-гими авторами. A, E_A – константы Аррениуса (определяются из эксперимента). Если использовать (2) при описании скорости химии-ческого процесса, то она дает хо-рошее согласие с экспериментом. Позже формула получила обосно-вание в самых различных теориях.

A, E_A можно найти, если обрабо-тать результаты эксперимента в координатах: .Из (2): (2’) (рис43)

Точки спрямляются согласно (2’).

. действительно будут константами, но в опреде-ленном интервале температур. Поэтому при их определении сле-дует указать интервал Т: . В таком случае по-лучается модифицированный за-кон Аррениуса:

,

. m требуется определять дополнительно.

Температурная чувствите-льность константы скорости химической реакции.

Если будем определять про-центное изменение k при изме-нении Т, то из (2) получим:

,

отсюда

.Если Т изменяется на 1%, т.е. , то

.Эта безразмерная величина определяет чувствии-тельность скорости химической реакции к изменению температу-ры. , , .

Чем больше Е и чем меньше T, тем больше чувствительность.

Эта величина большая для акти-вированных процессов.Посчитаем температурный коэффициент согласно закону Аррениуса:

.Если мало: , , то можно воспользоваться разло-жением экспоненты (e^x=1+x+…).

.

И если ΔT изменится на , то скорость химической реакции в этом интервале изменится в е раз. Последняя величина называется семеновским интервалом.