2. Модели состояния яркости изображений фона и объекта слежения

Для огромного количества возможных объектов очень трудно задать общее описание яркости в каждом элементе. Это достаточно сложно, поэтому мы будем использовать поточечное (поэлементное) описание для точек фона и объекта. Предполагается, что точки объекта являются связанными. Одним из простых способов описания является задание яркости каждой точки по отдельности.

Введем обозначения:

G_n – множество точек изображения фона размерностью N×N элементов;

G(n) – вектор, соответствующий этому изображению;

g(i, j, n) – яркости в точках (i, j) в n-м кадре.

G(n) = G(n– 1) (5.6)

Если фон является неподвижным и неизменным, пренебрегая эффектами дискретизации, можно записать

или, что то же самое,

Если считать начальное состояние G(0) случайным гауссовским вектором, то необходимо задать математическое ожидание m_G и ковариационную матрицу K_G этого вектора. Вектор G содержит N² элементов, а матрица K_G будет содержать N⁴ элементов.

Считается, что матрица K_G является диагональной с дисперсиями D_g на главной диагонали.

Модель, учитывающая возможные изменения яркости (температуры) во времени:

g(i, j, n) = g(i, j, n – 1) + ω(i, j, n–1), (5.7)

где ω(i,j,n–1) – N(0,D_ω) – процесс, некоррелированный во времени и протекающий независимо в каждой точке изображения

Изображение объекта представляет собой связное множество точек с соответствующими яркостями (две точки объекта считаются связанными, если они отстоят друг от друга не более чем на , где Δ – интервал пространственной дискретизации).

С течением времени яркость в различных точках изображения может изменяться каким-либо образом (может меняться температура, освещенность), возникает вопрос: как можно математически описать возможную изменчивость, если она носит случайный характер. Это можно сделать с помощью модели (5.7).

Такой процесс носит название случайного марковского процесса с независимыми приращениями (ω). Условно это можно нарисовать.

Возьмем точку на оси g(i, j). Далее яркость меняется и в процессе носит нестационарный характер (т.е. яркость то увеличивается, то уменьшается). В каждой точке в результате задания такой модели мы имеем марковский процесс, который протекает независимо в каждой точке изображения, что формирует неоднородное по пространству изображение.

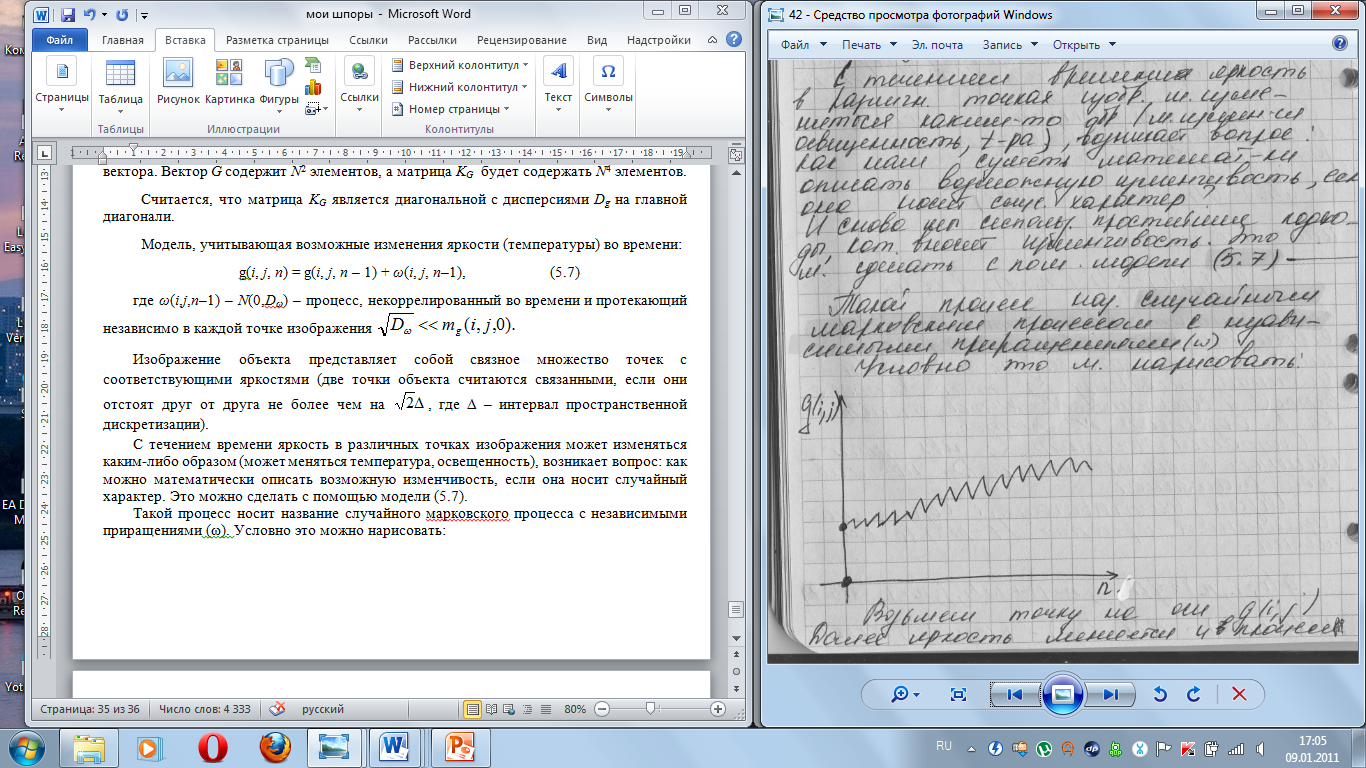
Если дисперсия D_ω=0, то мы получим постоянную (тоже, что и в начале). Если дисперсия мала, то мы будем иметь медленно меняющуюся по времени, если велика – то интенсивнее.

По отношению к объекту будем действовать также, как и к фону.

Определяем следующие яркостные модели для объекта:

1. Объект не движется, и яркости составляющих его точек постоянны во времени:

где h(i, j, n) – яркость объекта в точке (i, j) в n-м кадре.

2. Объект не движется, но яркости составляющих его точек могут изменяться во времени:

h(i, j, n) = h(i, j, n – 1) + η(i, j, n – 1), (5.9)

где η(i, j, n) – N(0, D_η) – процесс, некоррелированный во времени и протекающий независимо в каждой точке изображения.

Начальное значение h(i,j,0) – гауссовская случайная величина с известными средним и дисперсией.

3. Объект движется, но яркости составляющих его точек неизменны:

Где – смещение объекта вдоль осей координат за кадр.

Для описания изображения протяженного объекта оказывается удобным использовать наряду с введенной дискретной решеткой (x_i,y_j) вторую дискретную решетку (x_ν,y_μ), начало которой совпадает с точкой, ближайшей к центру непрерывного изображения объекта (рис. 5.2).

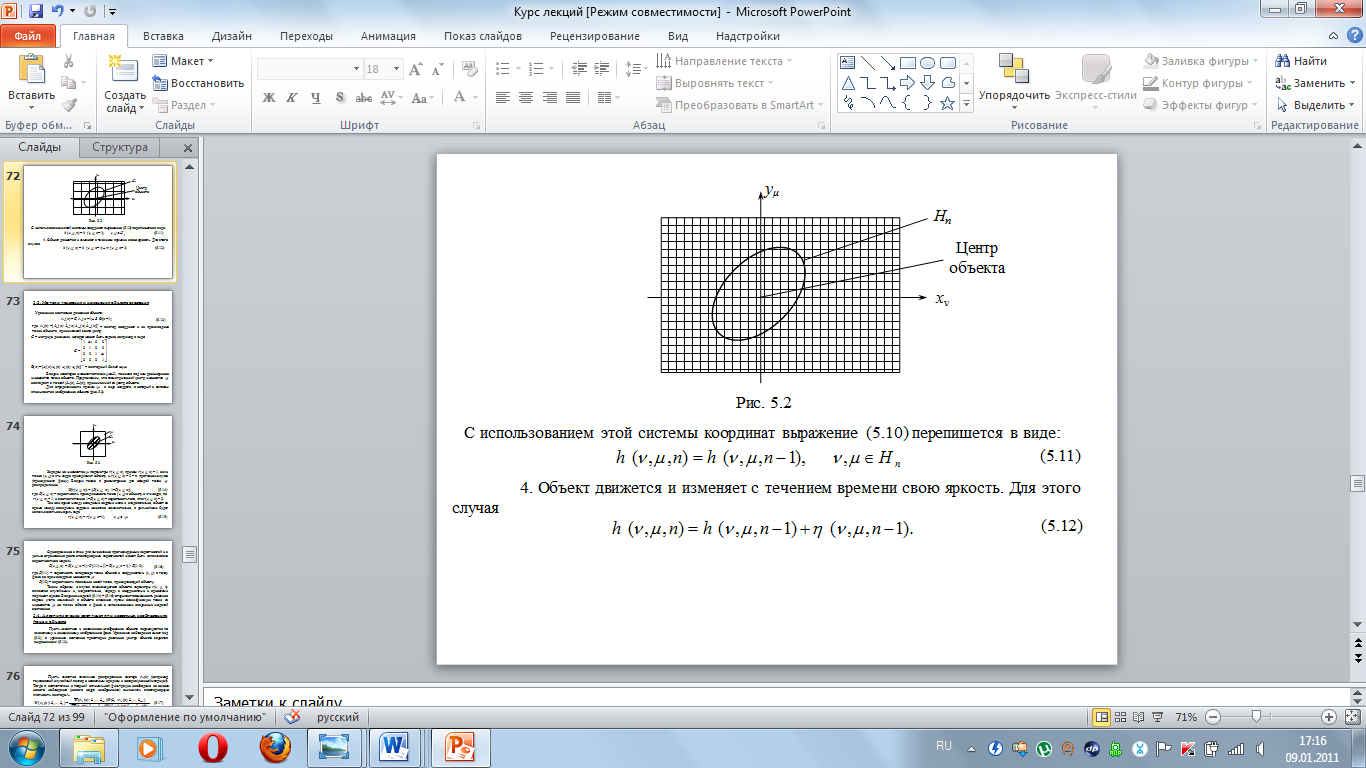
С использованием этой системы координат выражение (5.10) перепишется в виде:

4. Объект движется и изменяет с течением времени свою яркость. Для этого случая

10. Билет 1. Инверсная фильтрация. Винеровская фильтрация.

2. Модель движения и изменения объекта слежения.