2. Морфологическая операция выделения связанных компонентов

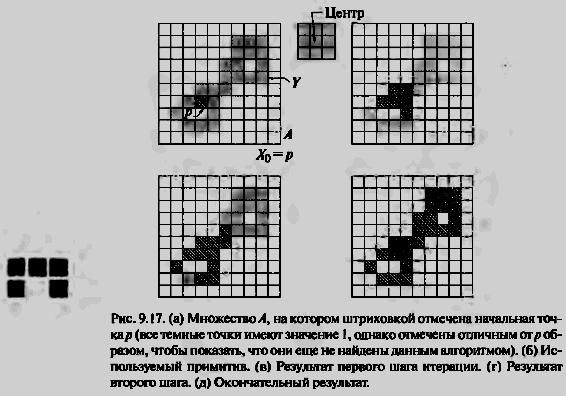
5. Билет 1. Описание дискретных изображений.

2. Корреляционные методы измерения координат объектов.

1. Описание дискретных изображений

Кадр изображения обычно представляется в виде матрицы F размерностью N₁xN₂, с элементами F(n₁,n₂). Однако часто удобно использовать векторное представление изображения. Введем для этого вспомогательный вектор V_n размером N₂х1 и матрицы N_n размером N₁N₂xN₁, определяемые следующим образом:

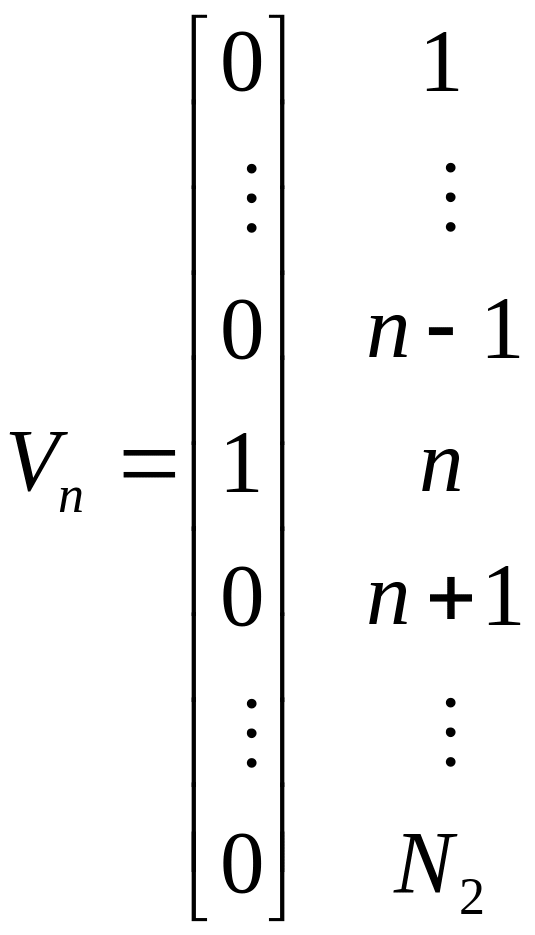
Пример.

В этом случае матрица F будет представлена в векторной форме с помощью операции упорядочения

Обратная операция преобразования вектора f в матрицу F описывается соотношением

При использовании статистического описания дискретных изображений начальные моменты определяются следующим образом:

т.е. среднее значение матрицы есть матрица, содержащая средние значения элементов.

Вектор выделяет n-столбец матрице , а матрица помещает этот столбец на место, отведенное для n-го участка вектора f. Таким образом, вектор f содержит все элементы матрицы , последовательно считанные по столбцам.

Если матрица разверткой по столбцам преобразована в вектор, то среднее значение этого вектора

Достоинством такого представления является возможность непосредственного использования методов, разработанных для обработки одномерных сигналов.

Корреляция двух элементов изображения с индексами (n₁, n₂) и (n₃, n₄) определяется как

Ковариация двух элементов изображения есть

Дисперсия элемента изображения

Если матрица изображения преобразована в вектор f, то корреляционную матрицу этого вектора можно выразить через корреляции элементов матрицы F

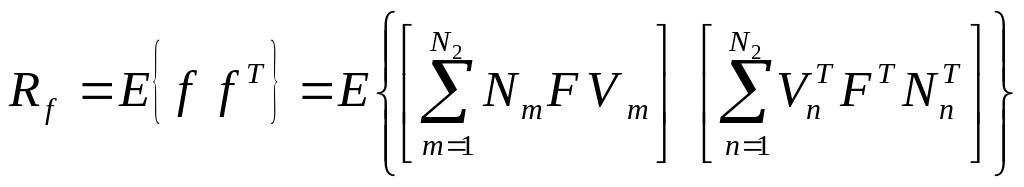
или

Выражение = R_m,n представляет собой корреляционную матрицу m-го и n-го столбцов матрицы F и имеет размер N₁xN₁. Таким образом, R_f можно представить в виде блочной матрицы

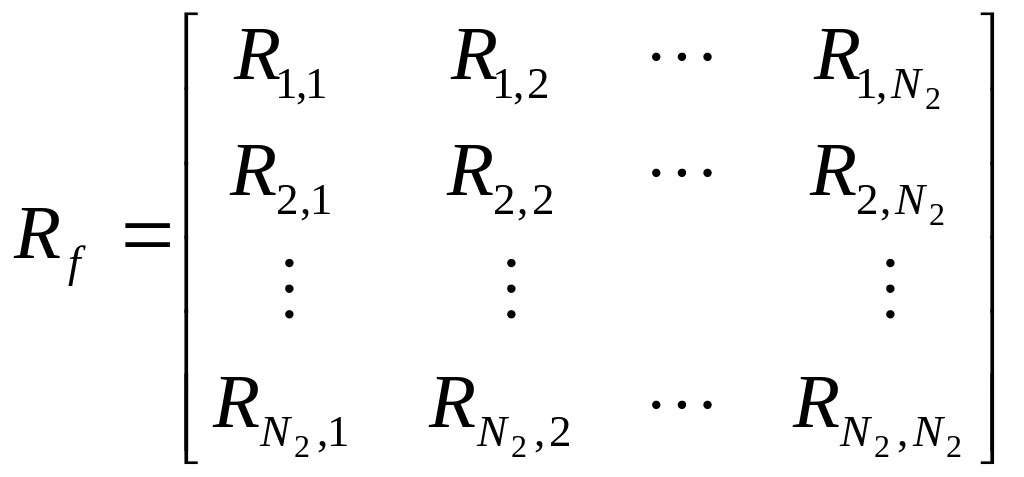
Ковариационную матрицу вектора f можно получить на основе его корреляционной матрицы и вектора средних значений с помощью соотношения

Матрица дисперсий V_F массива чисел F(n₁,n₂) по определению является матрицей, элементы которой равны дисперсиям соответствующих элементов массива. Элементы матрицы V_F можно непосредственно выделить из блоков матрицы K_f

Дискретное изображение, представленное вектором, можно полностью описать с помощью совместной плотности вероятности его элементов

где Q = N₁N₂ определяет порядок совместной плотности. В случае статистической независимости элементов изображения совместная плотность равна произведению одномерных безусловных плотностей

Наиболее распространенным видом совместной плотности вероятности является гауссова плотность

где K_f - определитель матрицы K_f.

2. Корреляционные методы измерения координат объектов

Для решения задач обнаружения, измерения координат, распознания объектов используются корреляционные методы, основанные на использовании информации о некотором эталонном изображении объекта.

Пусть имеется дискретное эталонное изображение объекта H, представляющее собой множество связанных элементов h(i,j) с некоторым условным центром, расположенным в начале координат. Наблюдаемое в некотором кадре изображение L описывается моделью вида

где Z_h – оператор, воздействующий на изображение объекта (оператор искажений);

ξ (i,j) – нормальный белый шум.

Часто Z_hможет вызыватьповорот изображения или изменять яркость объекта, изменять масштаб. Задача состоит в том, чтобы решать задачу измерения координат объекта, не смотря на эти изменения, искажения.

Мы ограничимся моделью, включающей смещение объекта вдоль осей координат. Тогда выражение (4.28) может быть представлено в виде

где α, β – параметры, характеризующие смещение центра объекта относительно начала координат. В (4.29) считается, что фон имеет нулевую яркость, т.е. имеется объект и шум на изображении.

Пусть нам известна , но мы не знаем, на каком месте находимся. С использованием статистических решений. Показано, что в этом случае оптимальным измерением координат объекта является вычисление взаимной корреляционной функции наблюдаемого и эталонного изображения объекта.

Пространственная взаимная корреляционная функция наблюдаемого изображения и эталонного изображения объекта:

Мы должны определить значения α^*, β^*, при которых достигается глобальный максимум выражения (4.30) . Эти значения будут определять положение центра объекта.

Если представить, что фон ненулевой, то мы можем получить не тот результат, а грубые ошибки, т.к., например, какая-то область изображения окажется яркой и мы умножим на большее значение яркости и получим значение, большее критерия. Чтобы ослабить этот эффект, используют нормированнуюую функцию вида (4.31).

Значения α^*, β^*, при которых достигается глобальный максимум выражения (4.30), принимаются в качестве величин, характеризующих смещение объекта вдоль осей координат.

Нормированная функция:

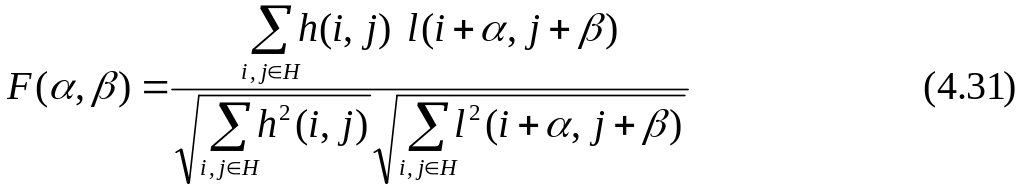
Еще один подход связан с разностными критериальными функциями, где уже нужно производить поиск глобального минимума.

Критериальные разностные функции:

Здесь находятся такие изображения, которые менее всего отличаются от эталонного. Влияние неравномерного фона уже меньше. Для абсолютно точного решения необходимо производить перебор всех α, β, а это требует огромного количества вычислений.

Пусть эталонный объект содержит 100*100 элементов, т.е. 10000 пикселей. Изображение, на котором мы хотим вести поиск 1000*1000 элементов, т.е. 1000000 возможных позиций, т.е. 10000 умножений и сложений. Получается, сто потребуется совершить не меньше 10 миллиардов операций в секунду. Поэтому и было разработано так много подходов для решения этих задач.

6. Билет 1. Изменение контраста и виды изменения гистограмм.

2. Метод последовательного определения сходства изображения