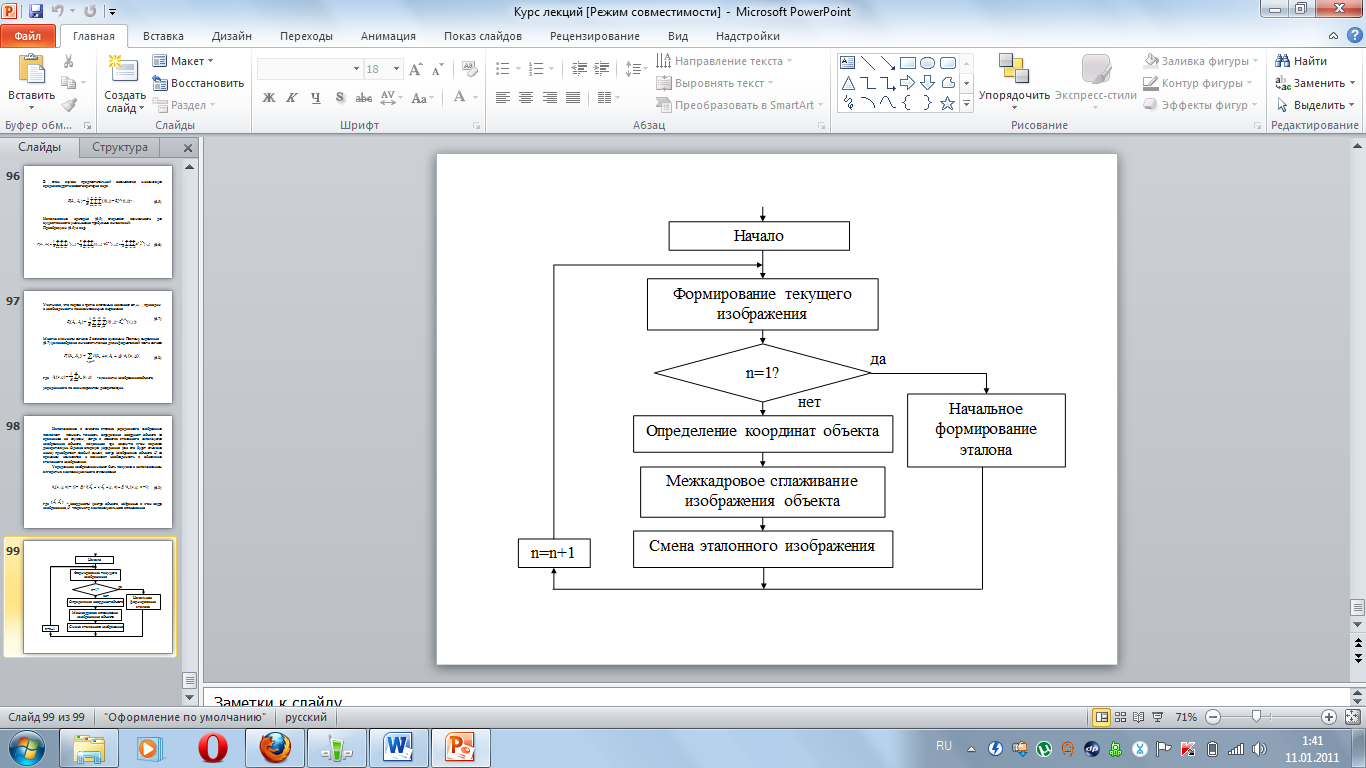
2.Алгоритм измерения координат с межкадровым усреднением текущего изображения объекта

В тех случаях, когда изображение объекта может изменяться с течением времени (изменение яркости, размеров, ракурса) требуется внесение изменений в текущее эталонное изображение объекта. В противном случае эталонное изображение (модель) перестает соответствовать текущему изображению объекта. Известно, что покадровая смена эталонного изображения ведет к накоплению ошибки измерения и как следствие к срыву слежения. При этом на точность измерения координат оказывают существенное влияние эффекты пространственной дискретизации изображений. Поэтому весьма желательно уменьшить их влияние на точность измерения.

Р ассмотрим вначале, каким образом можно уменьшить влияние пространственной дискретизации, полагая фон нулевым, а эталонное изображение объекта известным. Пусть в n-ом кадре имеется изображение L , представляющее собой, например, квадратную матрицу с элементами

И ндекс n для упрощения написания пока опустим. Будем считать, что это изображение представляет собой аддитивную смесь полезного сигнала S и шума. Информативная часть сигнала S, сигнал H, представляет собой квадратную матрицу с элементами. , М<N. Другие элементы сигнала S считаются равными нулю. Сигнал H представляет собой дискретное изображение объекта. В дальнейшем предполагается, что может быть K вариантов дискретизации объекта, получающихся смещением непрерывного изображения объекта относительно узлов дискретизации на величину не более половины шага дискретизации вдоль координатных осей. Под измеренными координатами центра сигнала H будем понимать точку дискретного изображения, в которой будет достигаться наилучшее совмещение текущего и эталонного дискретных изображений объекта. Центр сигнала H может быть расположен в любой точке сигнала S, но таким образом, чтобы все элементы сигнала H принадлежали бы сигналу S, как это показано на рис.6.1. Отметим, что вначале, точка, принимаемая за центр, считается заданной.

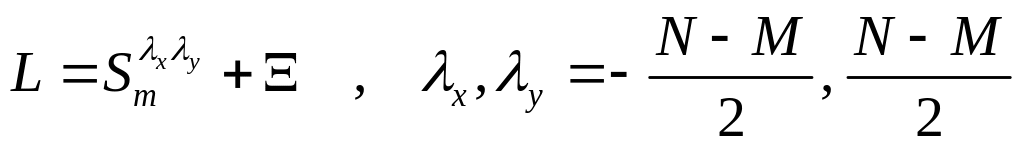
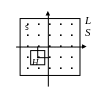
О бозначим через элементы изображения , полученные в результате m-го варианта дискретизации непрерывного изображения объекта, а через сигнал S , содержащий в себе сигнал Hm таким образом, что координаты центра сигнала Hm равны в системе дискретных координат, связанных с центром изображения L. Тогда можно записать, что наблюдаемое изображение L представляет собой

( 6.1)

где M и N являются четными величинами.

Рис.6.1. Изображения L, S, H

М ожно считать при этом, что сигналы L, , представлены в виде векторов, элементы которых упорядочены вполне определенным образом.

Обозначим априорную вероятность наличия сигнала как

Т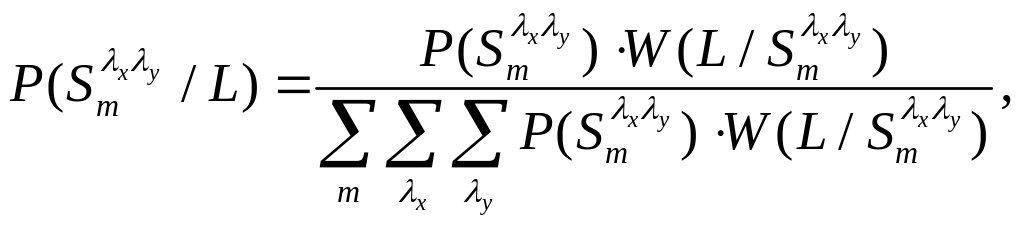 огда апостериорная вероятность наличия сигнала в наблюдаемой реализации L может быть вычислена с помощью формулы Байеса

(6.2)

Где - функция правдоподобия выборки.

А 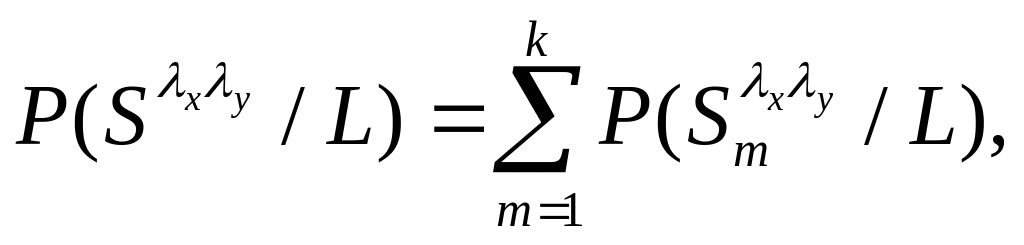постериорная вероятность наличия сигнала с центром в точке может быть вычислена как

(6.3)

П усть все варианты дискретизации объекта и расположения его центра равновероятны. Полагая полезный сигнал и помеху статистически независимыми, и считая, что все компоненты шума являются независимыми нормальными случайными величинами с нулевыми средними и дисперсиями ,будем искать оценки координат путем поиска максимума выражения

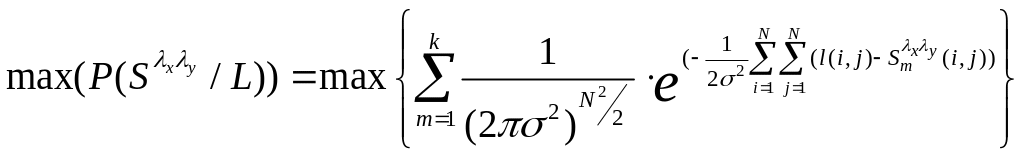
(6.4)

где - элементы сигнала .

Реализация алгоритма оценки, в соответствии с (6.4), в реальном масштабе времени может оказаться затруднительной, в связи с необходимостью вычисления экспонент и использованием многих эталонов.

В этом случае предпочтительней оказывается минимизация среднеквадратического критерия вида

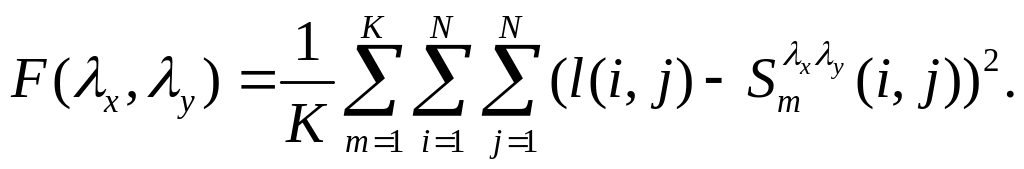
(6.5)

Использование критерия (6.5) открывает возможности для существенного уменьшения требуемых вычислений.

Преобразуем (6.5) к виду

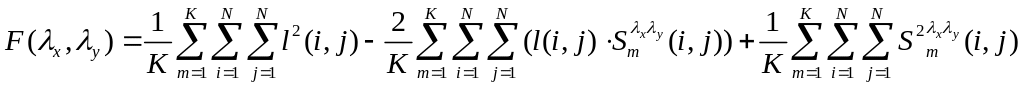
(6.6)

Учитывая, что первое и третье слагаемые не зависят от , приходим к необходимости поиска максимума выражения

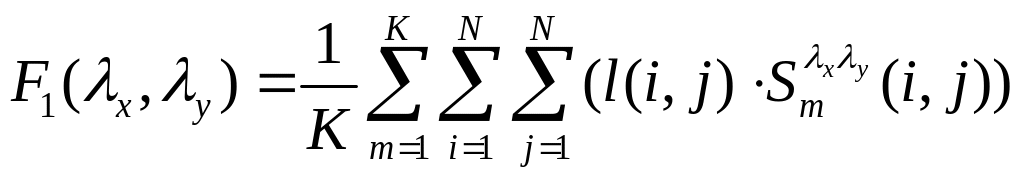
(6.7)

Многие элементы сигнала S являются нулевыми. Поэтому выражение (6.7) целесообразно вычислять только для информативной части сигнала

(6.8)

где - элементы изображения объекта, усредненного по

всем вариантам дискретизации.

Использование в качестве эталона усредненного изображения позволяет повысить точность определения координат объекта по сравнению со случаем, когда в качестве эталонного используется изображение объекта, полученное при каком-то m-ом варианте дискретизации. Однако операция усреднения (как это будет отмечено ниже) приобретает особый смысл, когда изображение объекта H со временем изменяется и возникает необходимость в обновлении эталонного изображения.

Усредненное изображение может быть получено с использованием алгоритма экспоненциального сглаживания

(6.9)

г де - координаты центра объекта, найденные в n-ом кадре изображения, -параметр экспоненциального сглаживания.

18 Билет 1. Морфологическая обработка. Базовые понятия теории множеств

2. Двумерное преобразование Фурье и его свойства