1. Пространственная реставрация методом псевдообращения матриц

Пусть наблюдаемое изображение моделируется интегралом суперпозиции

где F_I(,) и F_о(x,y) – функции, представляющие идеальное и нерезкое изображения соответственно;

J(x,y;,) – импульсный отклик.

Дискретный эквивалент соотношения (3.7) может быть представлен в виде матричного уравнения

g=Bf, (3.8)

где g – вектор размером P×1(P=M²), учитывающий M×M реальных отсчетов нерезкого изображения;

f – вектор размером Q×1 (Q=N²), учитывающий N×N псевдоотсчетов идеального изображения;

B – матрица размером P×Q, элементы которой представляют собой отсчеты импульсного отклика.

g – наблюдаемый вектор, В – модель искажающего явления, f- отсчеты некоторого исходного идеального изображения. Задача состоит в оценке вектора f. (3.8) – система линейных уравнений, в которых элементы вектора f являются неизвестными.

Число отсчетов наблюдаемого изображения Р будет меньше, чем число отсчетов идеального изображения, то есть меньше количества элементов в векторе f (P<Q). Получаем недоопределенную систему линейных уравнений (число неизвестных больше числа уравнений). Можно увеличить число отсчетов нерезкого изображения, то есть добиться того, что P>Q.

Задача реставрации сводится к нахождению такого, что

Проблема состоит в том, что это равенство практически никогда не выполняется, так как, с одной стороны, имеем дело с элементами реального изображения g, а элементы матрицы В определяются совершенно независимо на этапе формирования модели. Поэтому не гарантируется существование такого f, чтобы выполнялось (3.9).

Несовместность системы можно выразить в виде

g = Bf + e(f), (3.10)

где e(f) – вектор ошибки.

При несовместной системе уравнений решение ищется в виде

где W – линейный оператор, минимизирующий ошибку по критерию наименьших квадратов.

Если ранг матрицы В равен Q, то

Во многих изображающих системах идеальное изображение становится нерезким и, кроме того, повреждается аддитивным шумом. Связь наблюдаемого изображения с идеальным в этом случае можно записать в векторно-матричной форме:

g=Bf+n (3.13)

где вектор n состоит из двух аддитивных составляющих, одна из которых включает отсчеты аддитивного внешнего шумового процесса, другая – компоненты разности g–Bf, обусловленной ошибками моделирования при задании B.

Т.к. в вычислении участвует большое число элементов, наличие шума на изображении может приводить к возникновению больших ошибок в вычислениях.

Если известно, что аддитивный шум имеет нулевое среднее и ковариационную матрицу K_n, то оценка идеального изображения ищется в виде

где W – реставрирующая матрица, минимизирующая взвешенную ошибку

При P>Q матрица W имеет вид

2. Алгоритм измерения координат при известном изображении фона и объекта.

Пусть известное и неизменное изображение объекта перемещается по известному и неизменному изображению фона. Уравнение наблюдения имеет вид (5.3), а уравнение состояния траектории движения центра объекта задается выражением (5.13).

Пусть известно начальное распределение вектора Λ_h(n) (например, гауссовский случайный вектор с известным средним и ковариационной матрицей). Тогда в соответствии с теорией оптимальной фильтрации необходимо на основе нового наблюдения (нового кадра изображения) вычислить апостериорную плотность вектора Λ_h

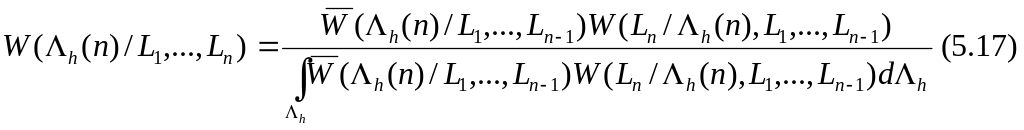
С учетом введенной модели шума при независимых наблюдениях

Считаем. Что распределение в каждой точке является гауссовским. Эта формула произведения гауссовых плотностей в каждой точке. S может принимать различные значения в зависимости от того, объект это или фон.

Байесовская оценка вектора Λ_h(n) при квадратичной функции потерь может быть получена как апостериорное среднее

Чтобы вычислить априорную (прогнозируемую) плотность для следующего кадра, необходимо ввести переходную плотность W(Λ_h(n)/Λ_h(n–1))

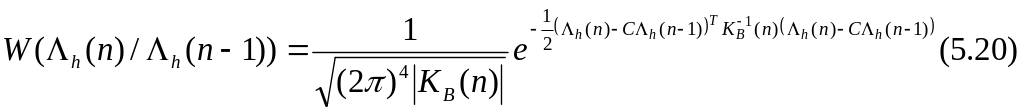
где |K_B(n)| – определитель ковариационной матрицы вектора BΘ(n).

Тогда прогнозируемая плотность может быть получена как

Таким образом, основные подходы к решению задачи состоят в следующем:

1. Вычисление прогнозируемой плотности в соответствии с (5.21).

2. Вычисление апостериорной плотности с использованием (5.17).

3. Вычисление апостериорного среднего в соответствии с (5.19).

Рассмотренный подход к решению задачи требует очень большого числа вычислительных операций ввиду многомерности вектора Λ_h, значительных размеров изображения L_n и необходимости вычислений в реальном масштабе времени.

12. Билет 1. Признаки методы выделения признаков.

2. Алгоритм оценки координат при известном изображении фона и объекта. Критерий максимума апостериорной плотности.