
- •1.Основные понятия и факты, связанные с д.У.
- •2.Существование,единственность и приближённое решение задачи Коши.
- •3. Д.У.,описывающие физические процессы (радиоактивный распад, гармонические колебания, падение тела и др.)
- •4.Приближенное построение интегральных кривых с помощью изоклин.
- •5.Уравнения с разделяющимися переменными и уравнения, сводящиеся к ним.
- •6.Линейные уравнения 1-го порядка.
- •7.Уравнения Бернулли и Риккати.
- •8.Уравнения в полных дифференциалах.
- •9.Интегрирующий множитель.
- •12.Уравнения Клеро и Лагранжа.
- •13.Уравнения высших порядков. Важнейшие случаи, допускающие решение в квадратурах либо понижение порядка.
- •14.Системы д.У. Метод исключения. Общий интеграл.
- •15.Линейные однородные уравнения в частных производных. Задача Коши.
- •16.Квазилинейные уравнения в частных производных. Задача Коши.
- •17.Линейная зависимость функций и вронскиан.
- •18.Линейные однородные уравнения. Линейная зависимость решений. Вронскиан решений.
- •19.Существование фундаментальной системы решений.
- •20.Формула общего решения линейного однородного уравнения.
- •21.Восстановление линейного однородного уравнения по ф.С.Р.
- •22.Формула Остроградского-Лиувилля.
- •23.Нахождение ф.С.Р. В случае постоянных коэффициентов уравнения.
- •24.Метод Лагранжа для линейных уравнений.
- •25.Метод неопределённых коэффициентов для линейных уравнений.
- •26.Линейные уравнения Эйлера.
- •27.Линейные однородные системы. Линейные системы.
- •29.Метод Лагранжа для линейных систем.
- •30.Метод неопределённых коэффициентов для линейных систем.
- •31.Задачи Коши и краевые задачи для линейных уравнений и систем.
- •32.Голоморфные решения линейных уравнений и систем.
- •33.Устойчивость решений. Система 1-го приближения. Критерий Рауса-Гурвица.
- •34.Фазовая плоскость. Обоснование одной(любой) из фазовых картин.
- •35.Линейные интегральные уравнения 2-го рода. Случай вырожденного ядра.
- •36.Задачи вариационного исчисления и понятие о способах их решения.
26.Линейные уравнения Эйлера.
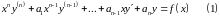
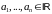
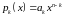
Т.е.
― линейное неоднородное уравнение с
особыми
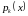 .
.
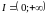 ― важен интервал.
Тогда можно
разделить на
― важен интервал.
Тогда можно
разделить на
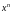 .
.
Однородное уравнение Эйлера:
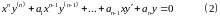
Определение: Определяющее уравнение для однородного уравнения
Эйлера ― следующее:
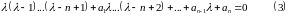
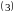 ― многочлен степени
относительно
― многочлен степени
относительно
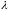 .
.
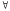 линейного однородного
уравнения надо знать фундаментальную
систему решений.
линейного однородного
уравнения надо знать фундаментальную
систему решений.
Теорема:
Для того, чтобы найти фундаментальную
систему решений
,
надо найти корни соответствующего
уравнения
вместе с их кратностями. Далее каждому
корню
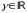 следует сопоставить функции:
следует сопоставить функции:
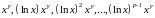 ,
где
,
где
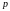 ― кратность
― кратность
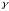 .
.
Каждой паре комплексных
сопряженных корней
уравнения
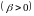 следует сопоставить функции
следует сопоставить функции
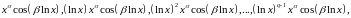
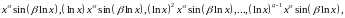
где
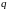 ― кратность корней
.
― кратность корней
.
Фундаментальную
систему решений
образуют функции, сопоставленные
указанным образом всем
корням
и всем парам
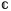 корней
.
корней
.
Для решения неоднородных уравнений Эйлера не существует универсальных методов: либо методом Лагранжа, либо неопределенных коэффициентов ― с соответствующими видоизменениями (сначала заменой ― линейное неоднородное уравнение).
27.Линейные однородные системы. Линейные системы.
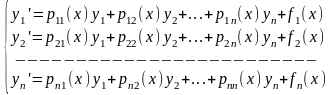 (1)
(1)
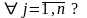
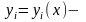 ?
?
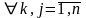
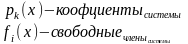
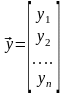 ,
,
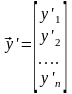 ;
;
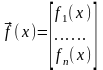 ;
;
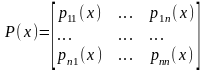
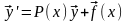 (1’)
(1’)
Если
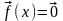 то (1) называется однородной системой,
иначе называется неоднородной.
то (1) называется однородной системой,
иначе называется неоднородной.
1.однородные системы

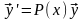 (2)
(2)
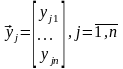 (3)
(3)
Опр:
Векторы (3) наз. лин. Зависимыми если
существуют такие
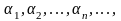 не все равные нулю, что
не все равные нулю, что
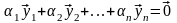 . Если это равенство справедливо лишь
при
. Если это равенство справедливо лишь
при
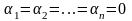 ,
то векторы называются лин. не зависимыми.
,
то векторы называются лин. не зависимыми.
Опр: фундаментальной системой решений системы (2) наз. совокупность n лин. нез. вект. является ее решениями
Опр: определителем Вронского или вронскианом (3) наз. определитель
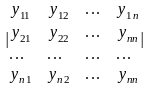 обозначение
Δ,Δ(x),
обозначение
Δ,Δ(x),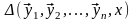
Теор1: пусть векторы (3) лин. зав. на I тогда Δ(x)≡0
Теор2: пусть векторы (3) реш. сист. (2) тогда справедливо одно и только одно утв.
А)Δ(x)≡0 (равносильно (3) л.з.)
B)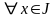
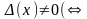 (3)
лин. независимо)
(3)
лин. независимо)
Теор3:
общее решение (2) имеет вид,
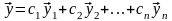 где
где
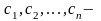 постоянные произведения, действительных
постоянные произведения, действительных
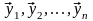 - ФСР (2)
- ФСР (2)
28.Линейные однородные системы с постоянными коэффициентами.(n=3)
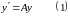 ,
,
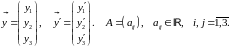
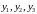 ― фундаментальная
система решений системы
(
― фундаментальная
система решений системы
(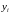 ― вектор !)
― вектор !)
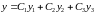 ― общее решение
.
― общее решение
.
Формулы для
фундаментальной системы решений разные
в зависимости от
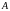 :
:
Собственные значения
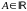 .
Можно указать три линейно независимых
собственных вектора матрицы
.
Можно указать три линейно независимых
собственных вектора матрицы
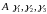 .
Тогда
.
Тогда
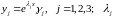 ― собственные значения
,
соответствующие
― собственные значения
,
соответствующие
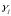 (
(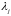 не обязательно различны)
не обязательно различны)Собственные значения . Можно указать три линейно независимых вектора
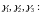
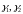 ― собственные
векторы
,
― собственные
векторы
,
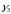 ― присоединенный вектор к собственному
вектору
― присоединенный вектор к собственному
вектору
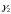 .
Тогда
.
Тогда
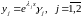 .
.
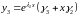 ,
где
,
где
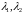 ― собственные значения, отвечающие
соответствующим
― собственные значения, отвечающие
соответствующим
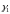 и
и
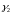 .
.
Собственные значения . Можно указать три линейно независимых вектора
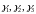 .
.
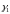 ― собственный вектор
,
― собственный вектор
,
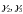 ― соответственно 1,2 присоединенные
векторы к
.
Тогда
― соответственно 1,2 присоединенные
векторы к
.
Тогда
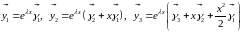 .
.
― собственное значение, соответствующее .
Пусть у существует одно собственное значение
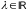 ,
два комплексно сопряженных собственных
значения
,
два комплексно сопряженных собственных
значения
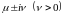 .
.
― какой-либо собственный вектор, отвечающий .
― какой-либо
собственный вектор, отвечающий
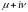 .
.
Тогда
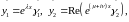
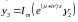 .
.
Для реализуется ровно 1 из 4 случаев.
