20.Формула общего решения линейного однородного уравнения.

Теорема 5. Формула общего решения (1) имеет вид: 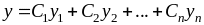(3) где 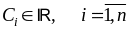– произвольные, принадлежащие 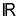числа, а 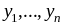– фундаментальная система решений.

Следствие: Уравнение (1) не может иметь больше линейно независимых решений.

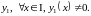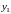
Теорема 6. Пусть дано Зная одно нетривиальное решение 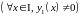уравнения (1), можно подстановкой 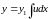понизить порядок уравнения, сохранив его линейность и неоднородность.

Теорема 7. – линейно независимые функции. . Тогда уравнение вида (1), для которого эти функции являются фундаментальной системой решений.

21.Восстановление линейного однородного уравнения по ф.С.Р.

Пусть дана система функций y1(x), y2(x), …, yn(x) с отличным от нуля на отрезке (a, b) вронскианом W(x). Требуется составить линейное однородное уравнение, у которого фундаментальная система решений состоит из функций y1(x), y2(x), …, yn(x).

Эта задача решается просто. Так как общее решение этого уравнения должно быть равно y(x) = C1 y1(x) + C2 y2(x) + …+ Cn yn(x), система функций y(x), y1(x), y2(x), …, yn(x) линейно зависима, поэтому её определитель Вронского (имеющий порядок n + 1) должен быть равен нулю

Раскрывая этот определитель по первому столбцу, получим искомое уравнение.

22.Формула Остроградского-Лиувилля.

Теорема 8.

Пусть 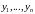– фундаментальная система решений (1), тогда справедлива формула: 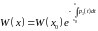(формула Остроградского-Лиувилля).

Доказательство:

Из теоремы 7: по ф.с.р. линейное однородное уравнение восстанавливается единственным образом, и это будет уравнение 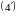. Сопоставляя и (1), получим: .

Далее воспользуемся формулой для производной определителя: .

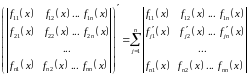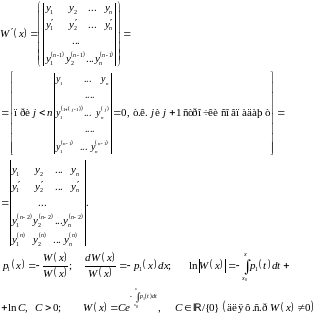
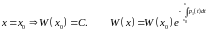
23.Нахождение ф.С.Р. В случае постоянных коэффициентов уравнения.

Найти все корни соотв. Хар-ко многочлена вместе с их кратностями каждому действ. корню 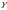поставить в соответствие функции ; k-кратность корня; ,

А каждой паре комплонарных сопряженных нужно сопоставить ф-цию:

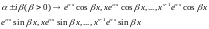
s-кратность каждого корня.

Функции указанным образом сопоставляются всем действительным корням и всем парам комплексн. Сопряж., образуют Ф.С.Р. Ур-ия (1)

Док-во:

Для частных случаев

1) все корни характеристического многочлена действительны и имеют кратность=1.

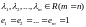
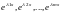-Ф.С.Р.

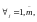
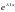подставим в (1)

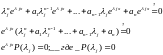
2) n=2

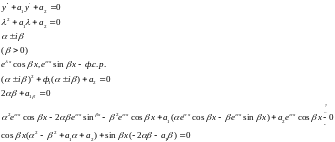
Где .

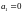24.Метод Лагранжа для линейных уравнений.

Метод Лагранжа (метод вариаций производных постоянных)

1) Составить и решить систему алгебраических уравнений

Доказательство:

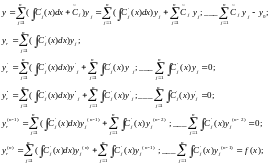
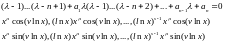Для

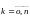
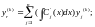
(и еще +f(x) для k=n )

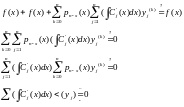
25.Метод неопределённых коэффициентов для линейных уравнений.

Метод неопределенных коэффициентов.

(Для уравнений с постоянными коэффициентами)

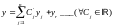
1)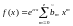 -квазимногочлен

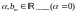
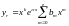
k=0, , если не является корнем соответствующего уравнения а если 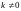, то берется кратности этого корня.

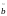берется неопределенное, а затем находится подстановкой в .

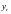2)

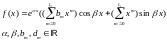
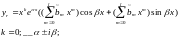
k=0, если 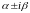― не корни соответствующего характеристического уравнения, равно кратности этих корней.

l=max(l1,l2)

Сначала 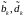― неизвестные. Находятся подстановкой в исходное уравнение.