
- •1.Основные понятия и факты, связанные с д.У.
- •2.Существование,единственность и приближённое решение задачи Коши.
- •3. Д.У.,описывающие физические процессы (радиоактивный распад, гармонические колебания, падение тела и др.)
- •4.Приближенное построение интегральных кривых с помощью изоклин.
- •5.Уравнения с разделяющимися переменными и уравнения, сводящиеся к ним.
- •6.Линейные уравнения 1-го порядка.
- •7.Уравнения Бернулли и Риккати.
- •8.Уравнения в полных дифференциалах.
- •9.Интегрирующий множитель.
- •12.Уравнения Клеро и Лагранжа.
- •13.Уравнения высших порядков. Важнейшие случаи, допускающие решение в квадратурах либо понижение порядка.
- •14.Системы д.У. Метод исключения. Общий интеграл.
- •15.Линейные однородные уравнения в частных производных. Задача Коши.
- •16.Квазилинейные уравнения в частных производных. Задача Коши.
- •17.Линейная зависимость функций и вронскиан.
- •18.Линейные однородные уравнения. Линейная зависимость решений. Вронскиан решений.
- •19.Существование фундаментальной системы решений.
- •20.Формула общего решения линейного однородного уравнения.
- •21.Восстановление линейного однородного уравнения по ф.С.Р.
- •22.Формула Остроградского-Лиувилля.
- •23.Нахождение ф.С.Р. В случае постоянных коэффициентов уравнения.
- •24.Метод Лагранжа для линейных уравнений.
- •25.Метод неопределённых коэффициентов для линейных уравнений.
- •26.Линейные уравнения Эйлера.
- •27.Линейные однородные системы. Линейные системы.
- •29.Метод Лагранжа для линейных систем.
- •30.Метод неопределённых коэффициентов для линейных систем.
- •31.Задачи Коши и краевые задачи для линейных уравнений и систем.
- •32.Голоморфные решения линейных уравнений и систем.
- •33.Устойчивость решений. Система 1-го приближения. Критерий Рауса-Гурвица.
- •34.Фазовая плоскость. Обоснование одной(любой) из фазовых картин.
- •35.Линейные интегральные уравнения 2-го рода. Случай вырожденного ядра.
- •36.Задачи вариационного исчисления и понятие о способах их решения.
15.Линейные однородные уравнения в частных производных. Задача Коши.
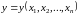
Линейные однородные уравнения
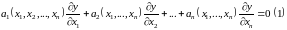
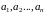 определены в
определены в
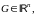 хотя бы одно
хотя бы одно
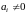 .
Пусть
.
Пусть
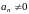 .
.
Определение: Системой в симметрической форме, соответствующей уравнению (1), называется система дифференциальных уравнений следующего вида:
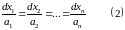
Придадим ей следующий
вид: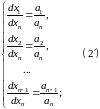
Теорема 1:
Для того, чтобы
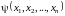 была решением (1), необходимо и достаточно,
чтобы
была интегралом (2).
была решением (1), необходимо и достаточно,
чтобы
была интегралом (2).
Теорема 2:
Формула общего решения (1) имеет вид
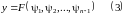 ,
где
,
где
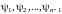 – независимые интегралы системы (2), а
– произвольная дифференцируемая
функция.
– независимые интегралы системы (2), а
– произвольная дифференцируемая
функция.
16.Квазилинейные уравнения в частных производных. Задача Коши.
Квазилинейные уравнения.
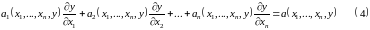 Решать
будем в неявном виде
Решать
будем в неявном виде

Продифференцируем
(5) по
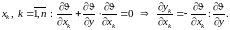
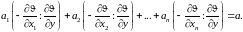
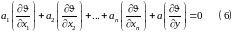
Решив (6), найдем
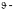 она и будет решением. Общее решение
уравнения (4):
она и будет решением. Общее решение
уравнения (4):
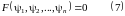 ,
где
,
где
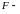 произвольная дифференцируемая функция,
произвольная дифференцируемая функция,
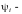 независимый интеграл системы в
симметричной форме, соответствующей
(6).
независимый интеграл системы в
симметричной форме, соответствующей
(6).
Определение:
Начальное условие для (1) и (4) –
следовательно, дополнительное условие:
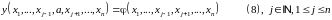 ,
,
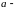 наперед заданное
число, принадлежащее
наперед заданное
число, принадлежащее
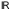 ,
,
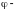 наперед заданная функция.
наперед заданная функция.
(1), (8) или (4), (8) – задача Коши.
17.Линейная зависимость функций и вронскиан.
Определение:
Функции
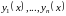 ,
определенные на интервале
,
определенные на интервале
 ,
называются линейно зависимыми на
,
если
,
называются линейно зависимыми на
,
если
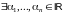 не все равные нолю, такие что
не все равные нолю, такие что
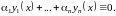 Если же тождество справедливо лишь при
Если же тождество справедливо лишь при
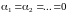 ,
то функции линейно независимы.
,
то функции линейно независимы.
Определение:
Определитель Вронского
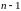 раз дифференцируемых функций
раз дифференцируемых функций
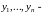 следующий определитель
следующий определитель
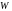 :
:
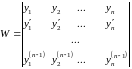
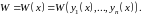
Теорема:
Если
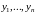 линейно зависимы и
линейно зависимы и
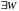 на
,
то
на
,
то
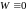 .
.
Следствие: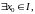
 линейно независимы.
линейно независимы.
Следствие:
Многочлены равны
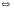 равны коэффициенты при одинаковых
степенях
.
равны коэффициенты при одинаковых
степенях
.
18.Линейные однородные уравнения. Линейная зависимость решений. Вронскиан решений.
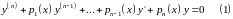
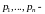 коэффициенты
уравнения;
коэффициенты
уравнения;
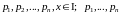 непрерывны.
непрерывны.
Краткая запись (1):
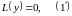 .
.
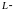 линейный оператор.
линейный оператор.
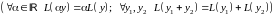 .
.
Т.к. справа ноль, то уравнение однородное.
Свойства:
1.
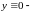 решение (1)
решение (1)
Линейная комбинация с любыми коэффициентами любых решений (1) – решение (1).
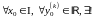 решение
уравнения (1),
решение
уравнения (1),
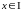 такое,
что
такое,
что
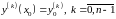 .
.
Теорема 1:
Пусть
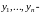 решения
уравнения (1);
решения
уравнения (1);
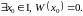 Тогда
линейно зависимы.
Тогда
линейно зависимы.
Доказательство:
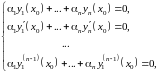
Определитель этой системы –
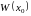
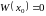
Тогда существует
нетривиальное решение. Выберем конкретное
нетривиальное решение системы
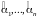 .
По свойству 2
.
По свойству 2
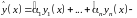 тоже
решение. Выберем
тоже
решение. Выберем
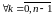 .
.
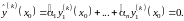 Наше решение в точке
удовлетворяет начальным условиям. С
другой стороны,
Наше решение в точке
удовлетворяет начальным условиям. С
другой стороны,
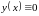 тоже удовлетворяет условию
тоже удовлетворяет условию
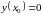 .
По свойству 3
.
По свойству 3
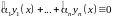 .
Т. к. не все
.
Т. к. не все
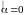 ,
то
линейно зависимы, ЧТД.
,
то
линейно зависимы, ЧТД.
Теорема 2. Пусть – решение (1). Тогда справедливо ровно 1 из следующих утверждений:
1.
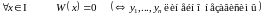
2.
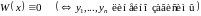
Доказательство:
Обоснуем, что не может где-то
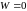 ,
а где-то не равняться.
,
а где-то не равняться.
Пусть
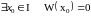 .
Тогда
линейно зависимы, т. е.
.
Тогда
линейно зависимы, т. е.
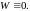
 линейно независимы.
линейно независимы.
От противного. Если
бы были линейно зависимы, то по теореме
из предыдущего вопроса
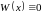 .
.
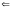 Если
бы
Если
бы
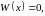 то
линейно зависимы.
то
линейно зависимы.
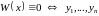 линейно зависимы.
линейно зависимы.
 От противного.
От противного
От противного.
От противного
19.Существование фундаментальной системы решений.
Определение: Фундаментальной системой решений (1) называется совокупность его линейно независимых решений.
Теорема 3. Для уравнения (1) существует фундаментальная система решений.
Доказательство:
Возьмем числа
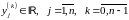 .
Потребуем, чтобы
.
Потребуем, чтобы
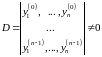 .
Обозначим
.
Обозначим
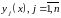 такие решения (1), для которых
такие решения (1), для которых
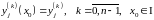 .
По свойству 3 с любыми начальными
условиями решение в
существует. Тогда
.
По свойству 3 с любыми начальными
условиями решение в
существует. Тогда
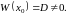 По теореме 2
По теореме 2
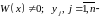 линейно независимы, т.е. фундаментальная
система решений.
линейно независимы, т.е. фундаментальная
система решений.
(замечания) общего метода для нахождения фундаментальной системы решений не существует.
Каждое (1) имеет бесконечное количество фундаментальных систем решений.
Частный случай (1): когда
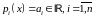 – числа
– числа
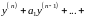

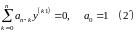
Определение:
Характеристическим уравнением для (2)
называется следующее выражение:
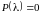 ,
где
,
где
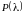 – характеристический многочлен (2):
– характеристический многочлен (2):
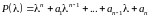 .
.
Свойства (и для любого многочлена):
1.
с точностью до порядка множителей
представление
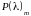 в виде следующих произведений:
в виде следующих произведений:
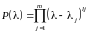 ,
где
,
где
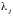 попарно различные, вообще говоря,
комплексные числа, которые называются
корнями многочлена, а
попарно различные, вообще говоря,
комплексные числа, которые называются
корнями многочлена, а
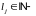 кратности
корней, причем
кратности
корней, причем
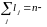 степень
многочлена. (Основная теорема алгебры)
степень
многочлена. (Основная теорема алгебры)
2.
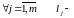 кратность
корня
кратность
корня
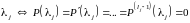 ,
причем
,
причем
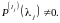
3. Два любых комплексно-сопряженных числа одновременно либо не являются корнями , либо являются, причем одинаковой кратности.
Теорема
4. Фундаментальную
систему решений (2) образуют функции,
сопоставленные всем действительным
корням и всем парам комплексно-сопряженных
корней соответствующих
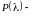 корням
многочлена, следующим образом:
корням
многочлена, следующим образом:
Если
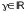 корень
кратности
корень
кратности
 ,
то ему следует сопоставить
,
то ему следует сопоставить
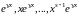 .
.
Если
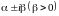 –
пара комплексно-сопряженных корней
кратности
–
пара комплексно-сопряженных корней
кратности
 ,
то им следует сопоставить
,
то им следует сопоставить
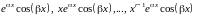 –
для
–
для
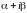
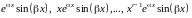 –
для
–
для

Теорема 7.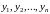 –
линейно независимые функции.
–
линейно независимые функции.
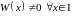 .
Тогда
уравнение вида (1), для которого эти
функции являются фундаментальной
системой решений.
.
Тогда
уравнение вида (1), для которого эти
функции являются фундаментальной
системой решений.
