
- •1.Основные понятия и факты, связанные с д.У.
- •2.Существование,единственность и приближённое решение задачи Коши.
- •3. Д.У.,описывающие физические процессы (радиоактивный распад, гармонические колебания, падение тела и др.)
- •4.Приближенное построение интегральных кривых с помощью изоклин.
- •5.Уравнения с разделяющимися переменными и уравнения, сводящиеся к ним.
- •6.Линейные уравнения 1-го порядка.
- •7.Уравнения Бернулли и Риккати.
- •8.Уравнения в полных дифференциалах.
- •9.Интегрирующий множитель.
- •12.Уравнения Клеро и Лагранжа.
- •13.Уравнения высших порядков. Важнейшие случаи, допускающие решение в квадратурах либо понижение порядка.
- •14.Системы д.У. Метод исключения. Общий интеграл.
- •15.Линейные однородные уравнения в частных производных. Задача Коши.
- •16.Квазилинейные уравнения в частных производных. Задача Коши.
- •17.Линейная зависимость функций и вронскиан.
- •18.Линейные однородные уравнения. Линейная зависимость решений. Вронскиан решений.
- •19.Существование фундаментальной системы решений.
- •20.Формула общего решения линейного однородного уравнения.
- •21.Восстановление линейного однородного уравнения по ф.С.Р.
- •22.Формула Остроградского-Лиувилля.
- •23.Нахождение ф.С.Р. В случае постоянных коэффициентов уравнения.
- •24.Метод Лагранжа для линейных уравнений.
- •25.Метод неопределённых коэффициентов для линейных уравнений.
- •26.Линейные уравнения Эйлера.
- •27.Линейные однородные системы. Линейные системы.
- •29.Метод Лагранжа для линейных систем.
- •30.Метод неопределённых коэффициентов для линейных систем.
- •31.Задачи Коши и краевые задачи для линейных уравнений и систем.
- •32.Голоморфные решения линейных уравнений и систем.
- •33.Устойчивость решений. Система 1-го приближения. Критерий Рауса-Гурвица.
- •34.Фазовая плоскость. Обоснование одной(любой) из фазовых картин.
- •35.Линейные интегральные уравнения 2-го рода. Случай вырожденного ядра.
- •36.Задачи вариационного исчисления и понятие о способах их решения.
12.Уравнения Клеро и Лагранжа.
5) Частный случай (6)
 ― уравнение Клеро.
― уравнение Клеро.

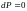
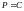
 - общее решение
уравнения Клеро
- общее решение
уравнения Клеро
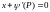
 особое решение
уравнения Клеро
особое решение
уравнения Клеро
6)
 ― уравнение
Лагранжа
(частный случай
― уравнение
Лагранжа
(частный случай
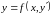 )
)
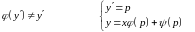

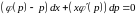
 ― линейное
уравнение
― линейное
уравнение
13.Уравнения высших порядков. Важнейшие случаи, допускающие решение в квадратурах либо понижение порядка.
 ― уравнение порядка
, разрешенные относительно старшей
производной.
― уравнение порядка
, разрешенные относительно старшей
производной.
Обычно решение ―
совокупность функций, зависящих от
произвольных постоянных.
 .
.
Общее решение: .
Частное решение ―
общее с конкретными
 .
.
Особое решение ― которое не получается из общего приданием значений константам.
Дополнительные условия:
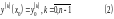 ― начальные условия.
― начальные условия.
 ,
,
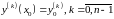 ―
задача Коши
―
задача Коши
Теорема:
Пусть в некоторой окрестности точки
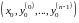 являются непрерывными функции
являются непрерывными функции
 .
Тогда в некоторой окрестности точки
.
Тогда в некоторой окрестности точки
 единственное решение задачи Коши.
единственное решение задачи Коши.
Далее ― о частных случаях.
или
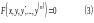
1)

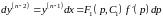
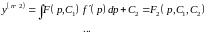
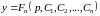
Ответ:
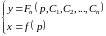
2) Предположим,
что в
 ,
тогда
,
тогда
 –уравнение
в точных производных.
–уравнение
в точных производных.
 –
не обязательно решается, но лучше тем,
что порядок его на единицу меньше. В
общем случае неизвестно, как находить
–
не обязательно решается, но лучше тем,
что порядок его на единицу меньше. В
общем случае неизвестно, как находить
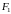 .
.
3)
Пусть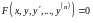 в у
в у
 существует свойство:
существует свойство:
 .
.
 .
Свойство однородности функции
относительно
.
Свойство однородности функции
относительно
 (
( –
степень однородности). Тогда порядок
(3) можно понизить на 1.
–
степень однородности). Тогда порядок
(3) можно понизить на 1.
Замена:
 ,
,

…

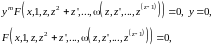
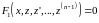 - решается не всегда.
- решается не всегда.
4)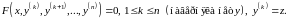
 .
.
Проинтегрировав
 раз, получим решение. Но решение для
может быть другим: в неявном виде,
параметрическом виде
раз, получим решение. Но решение для
может быть другим: в неявном виде,
параметрическом виде
5)


 (или параметрически). Вместо
–
(или параметрически). Вместо
–
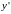 .
.
14.Системы д.У. Метод исключения. Общий интеграл.
уравнений с
неизвестными.
 .
.
Формы записи:
1. Нормальная:
 (1)
(1)
2. Симметричная:
 (2)
(2)
– система уравнений.
Легко переводятся одна в другую:
из (2) в (1):

из (1) в (2):
 .
.
Решение – совокупность
функций, в этой совокупности присутствуют
производных постоянных:
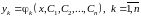 .
.
Константы – одни и те же для любых .
Начальные условия:
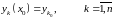 (3).
(3).
((1) или (2)) и (3) – задача Коши.
Теорема:
Пусть в окрестности точки
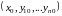 существуют и непрерывны
существуют и непрерывны
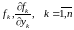 .
Тогда в некоторой окрестности
.
Тогда в некоторой окрестности
 решение задачи Коши (1), (3).
решение задачи Коши (1), (3).
Метод исключения.
После исключения
получаем уравнение большего
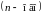 порядка. Не всегда можем исключать
функции. Общий случай для этого метода.
порядка. Не всегда можем исключать
функции. Общий случай для этого метода.
 .
Дифференцируем:
.
Дифференцируем:
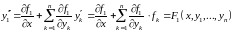
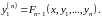
Получим
штук равенств, которые связывают
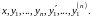 Будем исключать
Будем исключать
 Выберем
Выберем
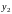 из равенства №1, подставляем во все
остальные равенства. Выбираем
из равенства №1, подставляем во все
остальные равенства. Выбираем
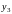 из равенства №2, подставляем во все
остальные.
из равенства №2, подставляем во все
остальные.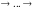 Получаем дифференциальное уравнение
-го
порядка (будет содержать
Получаем дифференциальное уравнение
-го
порядка (будет содержать
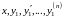 ).
).

Определение:
интеграл системы (1) – непрерывная
дифференцируемая функция
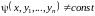 ,
дифференциал которой, вычисленный в
силу системы (1), тождественно равен
нолю, т. е.
,
дифференциал которой, вычисленный в
силу системы (1), тождественно равен
нолю, т. е.
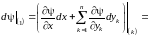 [вычисленный
в силу системы – значит, что
[вычисленный
в силу системы – значит, что
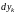 находят из равенств системы (1), т.е.
находят из равенств системы (1), т.е.
 ]=
]=
 .
.
Определение:
Первый интеграл системы (1) – соотношение
 ,
где
,
где
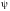 – интеграл системы (1), а
– интеграл системы (1), а
 .
.
Определение:
Интегралы системы (1)
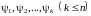 – независимые, если
– независимые, если
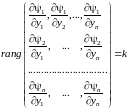 .
.
Определение:
Общий интеграл системы (1) – совокупность
его первых интегралов
 ,
для которых соответствующие интегралы
независимы.
,
для которых соответствующие интегралы
независимы.
Система (1) считается решенной, если найден её общий интеграл. (Общий интеграл – аналог решения в неявном виде.) Общий интеграл удобно находить для систем в симметричной форме, т. к. тогда удобно использовать свойство равных дробей:
Если
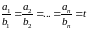 ,
то для
,
то для

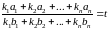 .
.
