- •1.Основные понятия и факты, связанные с д.У.
- •2.Существование,единственность и приближённое решение задачи Коши.
- •3. Д.У.,описывающие физические процессы (радиоактивный распад, гармонические колебания, падение тела и др.)
- •4.Приближенное построение интегральных кривых с помощью изоклин.
- •5.Уравнения с разделяющимися переменными и уравнения, сводящиеся к ним.
- •6.Линейные уравнения 1-го порядка.
- •7.Уравнения Бернулли и Риккати.
- •8.Уравнения в полных дифференциалах.
- •9.Интегрирующий множитель.
- •12.Уравнения Клеро и Лагранжа.
- •13.Уравнения высших порядков. Важнейшие случаи, допускающие решение в квадратурах либо понижение порядка.
- •14.Системы д.У. Метод исключения. Общий интеграл.
- •15.Линейные однородные уравнения в частных производных. Задача Коши.
- •16.Квазилинейные уравнения в частных производных. Задача Коши.
- •17.Линейная зависимость функций и вронскиан.
- •18.Линейные однородные уравнения. Линейная зависимость решений. Вронскиан решений.
- •19.Существование фундаментальной системы решений.
- •20.Формула общего решения линейного однородного уравнения.
- •21.Восстановление линейного однородного уравнения по ф.С.Р.
- •22.Формула Остроградского-Лиувилля.
- •23.Нахождение ф.С.Р. В случае постоянных коэффициентов уравнения.
- •24.Метод Лагранжа для линейных уравнений.
- •25.Метод неопределённых коэффициентов для линейных уравнений.
- •26.Линейные уравнения Эйлера.
- •27.Линейные однородные системы. Линейные системы.
- •29.Метод Лагранжа для линейных систем.
- •30.Метод неопределённых коэффициентов для линейных систем.
- •31.Задачи Коши и краевые задачи для линейных уравнений и систем.
- •32.Голоморфные решения линейных уравнений и систем.
- •33.Устойчивость решений. Система 1-го приближения. Критерий Рауса-Гурвица.
- •34.Фазовая плоскость. Обоснование одной(любой) из фазовых картин.
- •35.Линейные интегральные уравнения 2-го рода. Случай вырожденного ядра.
- •36.Задачи вариационного исчисления и понятие о способах их решения.
6.Линейные уравнения 1-го порядка.
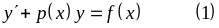 ― линейное
уравнение ―
уравнение такого вида
― линейное
уравнение ―
уравнение такого вида
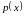 ― коэффициент
уравнения
― коэффициент
уравнения
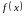 ― правая часть,
(неоднородность уравнения), свободный
член.
― правая часть,
(неоднородность уравнения), свободный
член.
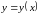 ― ?
― ?
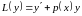 .
.
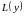 ― линейный оператор
― линейный оператор
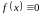 - однородное
- однородное
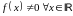 - неоднородное.
- неоднородное.
Свойства линейных уравнений:
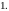 Общее решение
неоднородного линейного уравнения ―
сумма общего решения однородного
линейного уравнения и некоторого
частного решения неоднородного
Общее решение
неоднородного линейного уравнения ―
сумма общего решения однородного
линейного уравнения и некоторого
частного решения неоднородного
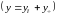 .
.
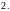 Сумма частных решений
однородного линейного уравнения ―
решение однородного линейного уравнения.
Сумма частных решений
однородного линейного уравнения ―
решение однородного линейного уравнения.
 Однородное
линейное уравнение
Однородное
линейное уравнение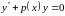 ,
,
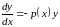 ,
,
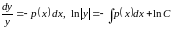 (
(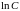 ― некая константа
― некая константа
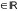 ,
,
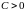 )
)
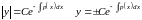
Т.к.
,
то
 .
Обозначим
.
Обозначим
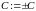 .
.
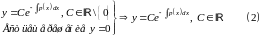
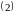 ― общее решение
однородного линейного уравнения
― общее решение
однородного линейного уравнения
Неоднородное
линейное уравнение
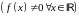 .
Для решения неоднородного линейного
уравнения существуют разные методы
(читать учебники).
.
Для решения неоднородного линейного
уравнения существуют разные методы
(читать учебники).
Метод Лагранжа (метод вариации произвольной постоянной):
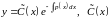 нужно подобрать.
нужно подобрать.
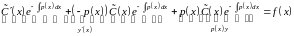
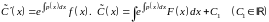
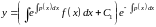 .
.
Нужно еще обосновать, что других решений нет
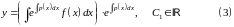
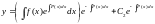
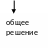

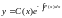
7.Уравнения Бернулли и Риккати.
Уравнения, сводящиеся к линейным:
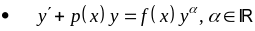 ― уравнение
Бернулли
― уравнение
Бернулли
Если
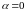 ,
то линейное неоднородное,
,
то линейное неоднородное,
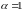 ,
то линейное однородное .
,
то линейное однородное .
Далее
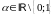 .
.
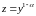 .
Делим уравнение Бернулли на
.
Делим уравнение Бернулли на
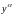 :
:
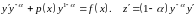 .
.
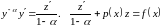 ― уже линейное
уравнение
― уже линейное
уравнение
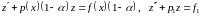 ― линейное уравнение
относительно
― линейное уравнение
относительно
 .
.
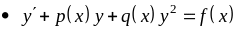 ― уравнение
Риккати
― уравнение
Риккати
Можно свести к
уравнению Бернулли, если известно
некоторое частное решение
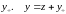 .
.
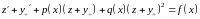
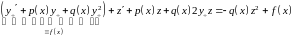
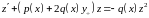 ― уравнение Бернулли
― уравнение Бернулли
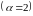
Не существует общего метода нахождения частного решения уравнения Риккати , поэтому в общем случае уравнение Риккати не решается в квадратурах.
Частный случай уравнения Риккати:
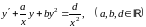 .
.
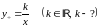
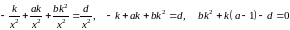 .
.
При
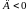 нужно искать другие частные решения.
нужно искать другие частные решения.
При
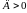 выбираем 1 частное решение.
выбираем 1 частное решение.
8.Уравнения в полных дифференциалах.
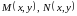 ―предположим, что
эти функции определены и непрерывно
дифференцируемы в некоторой односвязной
области (нет дырок)
―предположим, что
эти функции определены и непрерывно
дифференцируемы в некоторой односвязной
области (нет дырок)
Определение:
Уравнение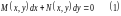 называется
уравнением полных дифференциалов, если
называется
уравнением полных дифференциалов, если
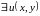 такая, что
такая, что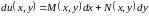 .
.
Уравнение можно
записать в виде:
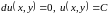 ―решение.
―решение.
Теорема:
Для того чтобы
,
для того чтобы
,
необходимо и достаточно, чтобы
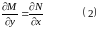
Из этих рассуждений
видно, что решение задачи с уравнением
полных дифференциалов сводится к
нахождению
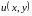 .
.
9.Интегрирующий множитель.
Предположим, что
уравнение
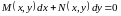 ―не уравнение полных дифференциалов
―не уравнение полных дифференциалов
Определение:
Интегрирующим множителем для уравнения
назовем
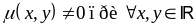 ,
после умножения на которую уравнение
становится полным дифференциалом.
,
после умножения на которую уравнение
становится полным дифференциалом.
Общего метода для нахождения интегрируемого множителя нет. Существуют различные методы:
1)
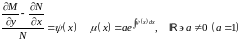
2)
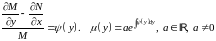 ,
,
3)
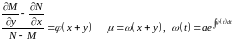 .
.
10.Уравнения
вида
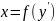 ,
y=
,
y=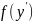 .
.
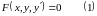
Если уравнение
разрешено относительно
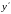 ,
т.е.
,
т.е.
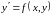 ,
то это частный случай
,
то это частный случай
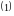
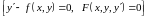 .
.
1)
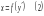 ― неполное уравнение, разрешенное
относительно
,
― неполное уравнение, разрешенное
относительно
,
(Т.к.
не входит
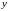 )
)
Вводим параметры:
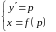 ―
параметрический вид
―
параметрический вид
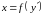
(Параметр ― вспомогательная независимая переменная)
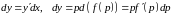
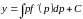
ответ:
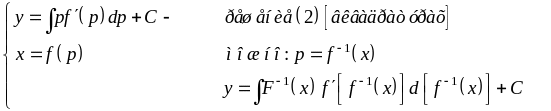
2)
 ― неполное уравнение, разрешенное
относ.
― неполное уравнение, разрешенное
относ.
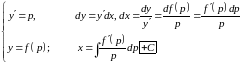
Ответ:
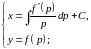
11.Уравнения
вида
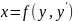 ,
y=
,
y=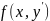 .
.
3)
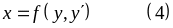 ―
уравнение, разрешенное относительно
―
уравнение, разрешенное относительно
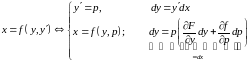
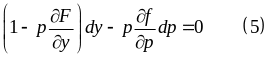
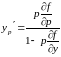 .
.
Ответ:
 ― решение , (параметрическое)
― решение , (параметрическое)
4)
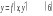 ― уравнение, разрешенное относительно
― уравнение, разрешенное относительно
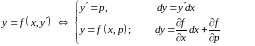
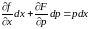 ,
,
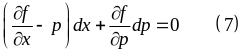
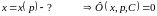
Ответ: